Elementary Number Theory

Good day fellow steemit readers, today we're going to talk about some basic concepts in elementary number theory.

Number theory is a branch of pure mathematics whose focus of the study is mainly integers. It is also known as the "Queen of Mathematics". Number theorists study prime numbers (which we have encountered before), and some properties of objects made out of integers.

The older term of number theory is arithmetic, a word used by the general public to mean "elementary calculations". This will be our focus today, we will do some elementary calculations.

This is the outline:

1. Even and odd
2. Decimal and base-n notation
3. Divisibility
4. Floor and Ceiling
5. Div and mod

---

Even and Odd

A simple definition of an even number is that if you divide the number by 2 you have no remainder. The word “even” is related to division. However, it turns out the concept is better understood if we relate it to multiplication.

Definition 1.1: an integer n is even exactly when there is an integer m such that n = 2m.

(What is an integer? Refer to previous posts.)

Note that there “two-way street” of looking at this definition. If a number is even, then we are guaranteed of the existence of another integer half as big. On the contrary, if we can show that another half as big number exists, then we know that the original number is even.

This kind of "two-wayness" of the definition is common in mathematics, it is known as a biconditional. We will revisit this concept in future posts.

Most people don’t believe that 0 should be considered an even number. Now that we have a precise definition, we can trace the correct answer to this question.

Is there an integer x such that 0 = 2x?

We did not say anything about n and m being distinct, so certainly zero is an even number with x = 0.

Any integer that is not even is certainly an odd number. That is, in the universe of integers, there are only two kinds of objects: even or odd. We can also craft some definition for odd without reference to “even”.

Definition 1.2: an integer n is odd exactly when there is an integer m such that n = 2m + 1.

Decimal and base-n notation

We can also define even and odd numbers by considering their decimal representation.

Take note, in a number each digit’s decimal representation depends on its position. Take for example the number 3482, we can write it as,

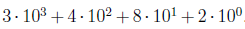
This is a familiar place notation where we use the power of 10, due to the fact that most humans have 10 fingers. The beauty of decimal representation is that it is possible to use any number in base of 10. For instance, in the field of computer science, they have the 3 common bases: 2 (binary), 8 (octal), and 16 (hexadecimal).

It is customary to append a subscript on a decimal representation to indicate what base is used. So, for example,

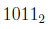
has a value of

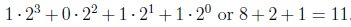
No matter what base we are using, the rightmost digit of the number multipliers the base raised to the 0-th power. Any number raised to the 0-th power is one, the rightmost digit is consequently known as the unit digit.

We can give another equivalent definition of even numbers base on its representation.

Definition 2.1: An integer is even if the unit digit in its decimal representation is one of 0, 2, 4, 6, or 8.
Definition 2.2: An integer is even if the unit digit in its binary representation is 0.

It is possible to develop general rules for converting a base-a number to a base-b number (where a and b are arbitrary) but it is actually more convenient to pick a “standard” base (we’ll going to use base 10 since we’re human) and develop methods for converting between an arbitrary base and the “standard” one.

Converting from one base to another is easy. You just have to use the definition of place notation. For example, to find what 451663 base 7 represents in decimal we write,

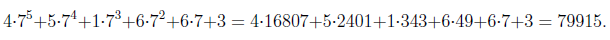
Converting from decimal to some other base is harder. It requires repeated division.

Divisibility

Another obvious definition of an even number is if whether we can divide it evenly. We need a notation for this. For this case, we will use a vertical bar – not a fraction bar.

The vertical bar when placed between two numbers is a symbol which asks the question: “Does the first number divide evenly (i.e. with no remainder) into the second?” On the other hand, the fraction bar asks directly for the value after carrying some division. (Note the importance of stressing the definition of each notation)

The value of 2|5 is false, whereas the value of 2/5 is 4.

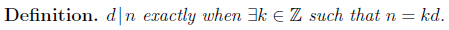
In the English language, the symbol d|n is translated in a variety of ways:

1. d is a divisor of n
2. d divides n evenly
3. d is a factor of n
4. n is an integer multiple of d

Let's look at some application of division.

Floor and ceiling

Assume we have men who all weight 200 pounds who want to use an elevator with a capacity of 1300 pounds. How many should ride at a time?

This is now a division problem, 1300/200 is 6.5; that is, 6.5 men should ride at a time. If there is a safety margin, we can’t round-up and let 7 men ride the elevator. This is an example of a problem that requires the use of floor function.

The floor function takes a real number as input and returns the next lower integer.

Here’s another situation:
Suppose after a party we have 43 unopened bottles of beer. We want to store them in containers that hold 12 bottles each. How many containers will we need?

This is, again, simply a division problem – 43/12 = 3.58333, which means we need 3 boxes and another 7/12 of a box. Obviously, we need 4 boxes, with one box having some unused space in it. In this sort of problem, we’re dealing with the ceiling function.

The ceiling function rounds a real number up to the next integer.

In standard mathematics textbooks, these functions are denoted using symbols that look very much like absolute value bars. The difference lies in some small horizontal strokes. If x is a real number, its floor is denoted by an absolute bar with horizontal stroke on the ‘floor’ of x, and its ceiling is denoted an absolute bar with horizontal strokes on the ‘ceiling’ of x.

Here are the formal definitions:
For floor function:

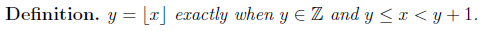
For ceiling function:

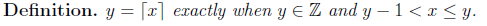
Div and Mod

In this section, we’ll discuss some more division algorithm. I know this sounds overkill. You know division already. In the U.S., long division is usually studied in the latter half of elementary school. However, we’re going to discuss this process in sordid detail because it gives us a good setting in which to prove relatively easy statements.
Suppose we have this division problem, n divided by some divisor d.

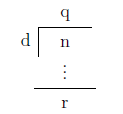
Recall that we have two parts in a division, a remainder r, and a quotient q. In some cases, r may be zero, but also, the largest r can be is d-1. Where did I get that assertion?

It comes from a well-known theorem known as the [quotient-remainder theorem]:

The words “div” and “mod” as shorthand for q and r, namely:

1. “n mod d” is a way of expressing the remainder r
2. “n div d” is a way of expressing the quotient q
   If two numbers, m and n, have the same remainder when you divide them by d, they are said to be congruent modulo d. We can express this by writing n mod d = m mod d but for shorthand notation,
   
   
   
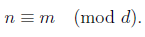
   (note how lazy mathematicians could be),

The operation “mod” operation is used quite a lot in mathematics. This is known as “modular arithmetic or, sometimes, “clock arithmetic”.

Here are some properties of modulo that will come in handy:

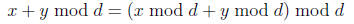
and

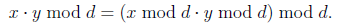
These rules mean that we can either do the operations first and then reduce the answer mod d or we can do the reduction mod d first and then do the operations.

For examples, consider we are working mod 10 on 87x96, we can instead just compute 7*6 mod 10, which is 2.

87x96 mod 10 = (87 mod 10x96 mod 10) mod 10
(87 mod 10x 96 mod 10) mod 10 = 7x6 mod 10
42 mod 10 = 2

References

1. https://en.wikipedia.org/wiki/Number_theory
2. https://www.khanacademy.org/computing/computer-science/cryptography/modarithmetic/a/the-quotient-remainder-theorem
3. https://www.csee.umbc.edu/~stephens/203/PDF/3-4.pdf
4. A Gentle Introduction to the Art of Mathematics by Joe Field

---

Thank you for reading ...