Mathematics - Mathematical Analysis Multivariable examples
Introduction
Hello it's a me again drifter1!
Today we will get into the promised examples/exercises for the whole Multivariable-part of my Mathematical Analysis series and so for every post starting from Vectors, Lines, Planes up to Surface and Contour Integrals.
I will try to solve them in detail so that you understand every bit of my procedure of thinking and why I apply each calculation, theorem etc.
Also, I will try "splitting" them based on the subtopic they are about...
So, without further do, let's get straight into it!
Vectors, Lines and Planes
Examples based on the posts:
1.
Suppose we have the following Planes/Surfaces.
E1: 5x + y - z = 10
E2: x - 2y + 3z = -1
What is the angle φ(E1, E2) between them?
The angle is of course equal to the same angle of the normal vectors N1 and N2 on top of surface E1 and E2 correspondingly.
That way we will find the angle φ(N1, N2) = φ(E1, E2).
Using the coefficients of x, y and z for each plane we can find the corresponding N'vectors and so:
N1 = (5, 1, -1)
N2 = (1, -2, 3)
The crossproduct of them gives us the following determinant:
which of course is the vector: (1, -16, 11)
And so:
Because the crossproduct is |ab| = |a||b|sinφ we find the angle like that:
2.
Suppose a surface E that:
- passes through P(4, 2, 1)
- is vertical across to N(6, -2, 3)
Calculate the distance of the center O(0, 0, 0) to the surface and so:
d(O, E) = ?
N is of course a normal vector of the plane and because the plane also passes from P we have:
6(x - 4) - 2(y - 2) + 3(z - 1) = 0 =>
E: 6x - 2y + 3z = 23
Let's suppose another point P'(x0, y0, z0) on top of the plane so that OP' is parallel to N.
This means that:
OP' x N = 0 =>
And so we end up with a system of 3 linear equations:
3y0 - 2z0 = 0
3x0 - 6z0 = 0
-2x0 - 6y0 = 0
Which means that:
z0 = 3y0/2 = 3x0/6
y0 = -2x0/6
and so because P' is on top of E we have:
By putting this values in the equations of before we end up with:
And because d(O, E) = d(O, P') we have:
Vector functions and Partial Derivatives
Examples based on the posts:
1.
Suppose the linear approximation of a curve r(t):
T = (dx/dt, dy/dt, dz/dt) = (1 + sint, 2cos(2t), -3sin(3t))
Find the line ε that:
- is vertical across to r(t)
- and that passes through Pt(x(t), y(t), z(t)) for t = π/2
For t = π/2:
T(π/2) = (1+1, -2, 3) = (2, -2, 3)
Because ε is vertical across it's parallel to the normal vector N.
We know that N = (∂r/∂x, ∂r/∂y, ∂r/∂z) and so:
N = (t - cost, 3tsin(2t), 1+cos(3t)) and for t = π/2 =>
N = (π/2, 3, 1)
And so from the parametric representation of a line we have:
x = x0 + at
y = y0 + bt
z = z0 + ct
By setting (x0, y0, z0) = (π/2, 3, 1) we get:
x = π/2 + π/2t
y = 3+3t
z = 1 + t
or
By using the normal vector N we can also find plane E that contains the Point Pt.
E: a(x - x0) + b(y - y0) + c(z - z0) = 0 => ... =>
2.
Suppose the function:
Calculate the range of Duf(P) = ∇T(P) * u at P = (0, 0)
We know that Duf(P) is between two values:
- The highest possible increase |∇f(P)| and
- The highest possible decrease -|∇f(P)|
cause Duf(P) = ∇f(P) * u = |∇f(P) ||u|*cosφ
and so the highest increase is when φ =0 and the highest decrease when φ = π
For the point (x, y) = (0, 0) this becomes: (1, 1)
And so the highest possible increase is:
The highest possible decrease is of course the negative of that...
And so the range of Duf(P) is:
3.
Suppose we have the total differential:
Find a function f (if it exists) that has this df.
From theory we know that:
df = Mdx + Ndy represents the total differential of a function f only if:
My = Nx <=> ∂M/∂y = ∂N/∂x
that can be easily proven...
Let's check if that is true...
We can clearly see that My = Nx and so there exists an f with this df.
Let's now find this function...
M = x + e^(x,/y) = ∂f/∂x =>
N = ∂f/∂y =>
and so:
Surface and Contour Integrals
Examples based on the posts:
1.
Calculate the surface integral:
The "inner" integral doesn't contain x and so is a "constant" which means that:
Because we have an subroot we substitute using:
y = 2sint => dy = 2costdt
which gets us to the range:
y -> 0 => t -> 0
y -> 2 => t -> π/2
and so:
cos^2t = 1 + cos(2t) / 2 and so:
2.
Tranform the contour integral to an Surface one:
Using Green's theorem we get:
Changing to the polar coordinate space we can also get:
Knowing the ranges of x and y (or r and θ) and so the Area R or G we can then calculate the actual value of I.
And this is actually it for today and I hope that you enjoyed those examples!
From next time in Mathematics we will get into a new "branch" of Mathematics :)
Bye!

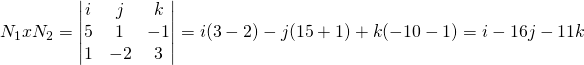
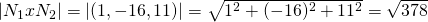
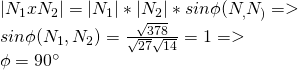
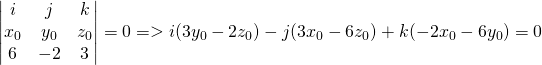
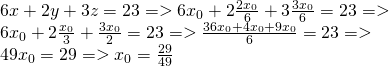
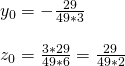

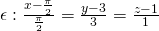
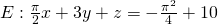
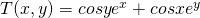
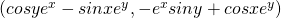
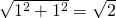
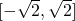
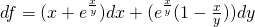
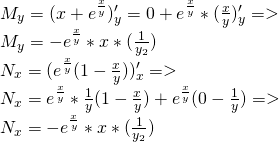
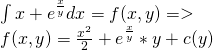
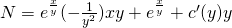
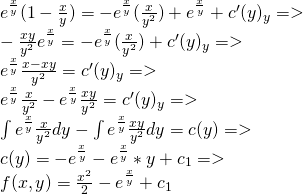
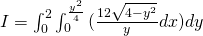
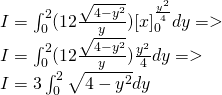
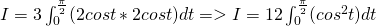
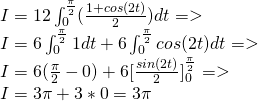
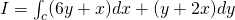
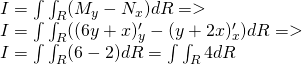
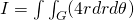
Very explicit. Just as a suggestion @drifter1...i would love you to add the immediate past publication of each particular series you write about:
something like...
PREVIOUSLY ON THIS SERIES:
Mathematical Analysis - Surface and Contour Integrals
Just for ease of navigation.
Yes, I'm trying to add the previous posts of those series, but sometimes I forget :P
Maybe I should do it from now on so that it becomes an habit...
Good approach. Your work is really great; i love all of it. I saw your recap post, it was really awesome! You have a new friend and follower! I will definitely be in touch with this blog.
Thank you! You are so kind.
Very happy to have you join my journey to the Moon...Ehmm I mean I'm glad that you enjoy my posts and I will be checking on your blog too, from time to time...
Seems like you also blog about great stuff :)
Thank you boss.
...woudn't know exactly what kinda contents appeal to you, but i definitely do what i gotta do, i just hope you like 'em.