Mathematics - Mathematical Analysis Vectors, Lines and Planes
Introduction
Hello it's a me again drifter1!
It's Easter Holiday time for me and so I got back home to chill for 2 weeks with my family and friends. In the first week I had some time for posting, but during the weekend we went to my Aunt and so I don't had time to post! But here I am again to post for you Steemians!
Today's topic is Mathematical Analysis again and more specifically Vectors and equations for Lines and Planes! I already covered a lot about Vectors during my Physics "category" and so I suggest you to read the post about it here. We will make a quick recap and then continue with some more things that I didn't had to talk about in Physics! After that we will get into Lines and Planes...
So, without further do, let's dive straight into it!
Quick recap
Vectors are arrows that point from one point to another and describe the direction of movement and also by how much we move in each of the x, y or even z coordinates in 1-, 2- or 3-dimensional space (meter).
From the Physics post (tweaked)...
Two vectors are equal when they have the same direction and meter.
The meter |A| of vector A is of course equal to:
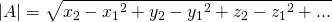
via quicklatex
where A = (P1P2) with P1 = (x1, y1, z1, ...) and P2 = (x2, y2, z2, ...)
Vectors can be analyzed into components for each axis.
We can of course do some operatios on vectors that include:
- Addition -> A + B = C
- Substraction -> A - B = D
- Scalar product -> A*B = |A| |B| cosφ and so a real number
- Cross product -> AxB = ABsinφ and so a new vector [calculated using a determinant]
To have a common language we use unit vectors for each axis of a linear space, where an unit vector has meter 1.
To make a vector into a unit vector (meter 1) you simply divide it with it's meter!
Vector tangents and normals
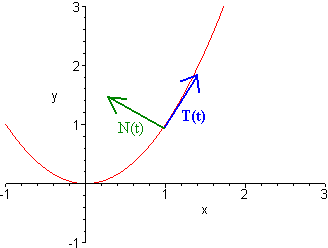
- A vector/line is tangent to an vector/line if they are parallel to each other.
- On the other hand it's a normal when they are vertically across.
To find a parallel (tangent) vector at a specific point of a line we simply find a unit vector with the same angle λ as the line. On the other hand for finding a normal vector we find a vector with angle -1/λ, but there is also a small trick if we already found the answer of the tangent.
Example
For the line 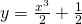 (quicklatex) at x = y = 1 we have:
(quicklatex) at x = y = 1 we have:
So, the vector we search for is:
v = 2i + 3j which has an angle of 3/2
The corresponding unit vector is:
This is the tangent at (1, 1).
We could also use the negatve vector -u.
For the normal vector we simply find the negative inverse of u.
To do that we swap the places of the components and change the sign of one of them.
So, a normal vector is:
Two more useful things are the following:
- Two vectors are across if the scalar product of them is zero (u.v = 0).
- Two vectors are parallel if the cross product of them is zero (uxv = 0)
Vector projection
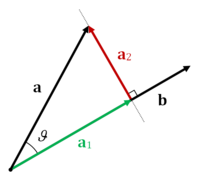
The vector projection of a vector u onto a line parallel to another non-zero vector v is the orthogonal projection of u straight into the line parallel to v.
From wikipedia
It can be noted as proj (u, v) which means projection of u onto v.
To calculate it we use:
proj (u, v) = |u|cosθ = u * v/|v|
where u*v is the scalar or dot product and θ the angle between u and v.
Cartesian coordination space
The Cartesian space is defined using 3 axes (x, y and z).
Each point P is represented using values given to each of those coordinates that represent the position on each axis.
The center of the space is O(0, 0, 0).
In this space we can define planes like:
- xy where each point has z = 0
- xz where each point has y = 0
- yz where each point has x = 0
Using even more restrictions we can define more an more subspaces if this Cartesian space.
As already shown before vectors are represented using:
u = OP = xi + yj + zk
where (x, y, z) is the point P and i, j, k are the unit vector on each axis.
The meter is of course equal to the square root of the squares on of each coordinate.
Using the same concept we can calculate the distance between two points P1 = (x1, y1, z1) and P2 = (x2, y2, z2) in space, as the meter of the vector P1P2.
The equation of distance is:
Lines in space
A line in space can be represented by only two things:
- A point of the line (P)
- The slope/angle λ
A straight line is simply y = λx.
For more complex ones we use two representations:
- Vector representation
- Parametric representation
Vector representation
A line L parallel to a vector v that surpasses the point P0 = (x0, y0, z0) is:
r(t) = r0 + i*v
where r is the position vector of the point P(x, y, z) of L and r0 is the position vector of the point P0.
Parametric representation
By taking the components of the previous one we end up with the parametric representation.
For a line that contains the point P0 = (x0, y0, z0) and is parallel to the vector v = u1i + u2j + u3k we have:
x = x0 + t*u1
y = y0 + t*u2
z = z0 + t*u3
where t is any real number.
So, to find a line we simply need to find a parallel vector to that line and need to know a point where the line passes by, cause the vector and line have the same slope/angle (tangent vector).
Planes in space
Using the same concept we can also define a plane.
A plane that contains the point P0(x0, y0, z0) and is vertically across to a vector n = Ai +Bj + Ck (normal) is of the form:
n*(P0P) = 0
or
A(x - x0) + B(y - y0) + C(z - z0) = 0
or
Ax + By + Cz = D where D = Ax0 + By0 + Cz0
So, to find a plane we just have to find a normal vector to that plane and have a point given.
Because the Plane types are more advanced I leave them for a post on their own...
And this is actually it and I hope that you enjoyed it!
Bye!
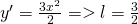 (
(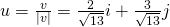 (
(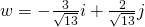 (
(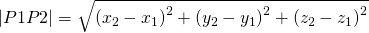 (
(
Just checking in after a hiatus, glad to see you are still at it. Was checking out the differential equations articles and found them really useful. Is this going to be a part of a Vector Calculus type series or still keeping it pretty general?
I try to write things in an easy way that can be understood by anyone, even those that dont know a lot of maths...
Mathematical Analysis is a series of its own and the posts that follow will be much more advanced then the first parts of this series that contained only limits, derivatives, integrals and series...
very cool looking forward seeing how the series develops
Very nice project, made me remember my math years in college.
It's very strange for me (non native English) to try to understand an English math demonstration :D
I appreciate your general public approach, I am still dreaming of complementary education done on Steemit :D
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by drifteritis from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.