Mathematics - Mathematical Analysis Advanced Plane Types
Introduction
Hello it's a me again drifter1! Today's topic is Mathematical Analysis again and we will continue our talk about Planes that we started in my previous post yesterday. I will get into some forms/types of planes and their corresponding equations in-depth so that you also understand more about what we discussed last time. So, I highly suggest you reading my previous post and be prepared for some more advanced stuff today!
So, let's get started!
A simple Example
Using the knowledge of last time let's get into an example...
Find the equation for the Plane that:
- contains the point P0(-3, 0, 7) AND
- has a normal vector n = 5i + 2j - k
From the second form ("or") of last time we have:
A(x - x0) + B(y - y0) + C(z - z0) = 0 =>
5(x + 3) + 2(y - 0) - (z - 7) = 0 =>
5x + 2y - z = -22
What if we don't know the vector?
If the normal vector is not given (most of the times this is the case) then we will have more then 1 points given to us.
With 3 points A, B and C given to us we find the normal vector by finding the crossproduct of vectors that contain A, B and C as start or endpoints.
For example:
AB x AC, where AB and AC are vectors.
Having A(0, 0, 1), B(2, 0, 0) and C(0, 3, 0) we get:
And so n = 3i + 2j + 6k is a normal vector to that plane.
That way the Plane can be found by using any of the points A, B or C as P0...
For example using A we get:
3(x - 0) + 2(y - 0) + 6(z - 1) = 0 =>
3x + 2y + 6z = 6
More stuff about Planes
After getting into those two characteristic examples, let's get into some more things...
We might be asked one of the following things:
- Find a vector that is parallel to the intercept of two planes
- Find the intercept point of a line and a plane
Finding the first one is simple, cause the intercept line will be vertically across to the normal vectors n1 and n2 of the two planes. That way it will be parallel to the cross product n1 x n2 and so any multiple of n1 x n2 will be vertical to the line.
The second one is also simple, cause we just have to solve the system of the two (or more) equations that represent the line and plane. The intercept point is a part of the line and plane and so using the parametric representation of a line we could just "insert" those equations into the plane equation to get the value of t. Putting the value of t to the x, y and z equations we then get the actual intercept point...
Cylinder Plane
A Cylinder is a plane that is build up of all the lines that:
- are parallel to a specific line
- pass through a specific (generator) curve
To understand a cylinder more we create cross-sections which are the "curves" that we get when cutting the cylinder with parallel planes.
Maybe the simplest one is the y = x^3 parabola cylinder.
Another interesting cylinder is the hyperbola cylinder which contains lines parallel to the hyperbola y^2 - z^2 = 1 in the plane yz ( x = 0).
So, a cylinder equation is any equation that contains 2 of the 3 cartesian coordinates and creates a cylinder parallel to the axis of the 3rd one.
2nd-degree Plane Equations
More advanced planes are build of 2nd-degree equations.
These planes are 3-dimensional and have the following general form:
where A, B, ... are constants.
Those equations can of course be simplified using rotations and commutations.
The Cylinders that we talked about previously are of course also of this form, but are a much simpler case!
The most important planes of this category are:
- Ellipsoids
- Paraboloids
- Elliptical cones
- Hyperboloids
Let's dive into each category separately...
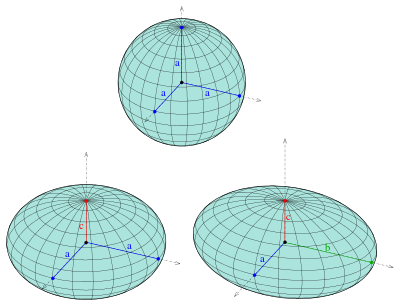
Ellipsoids
The sphere that we all know is of course a special case of an Ellipsoid...
An ellipsoid is represented using an equation of the form:
An ellipsoid of course intersects with the axes at the points:
- (+-a, 0, 0) for the x-axis
- (0, +-b, 0) for the y-axis
- (0, 0, +-c) for the z-axis
Having only two of the coordinates we end up with an ellipse and the elliptic equation:
where z = 0
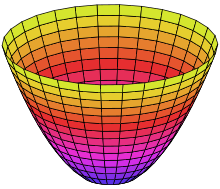
Paraboloids
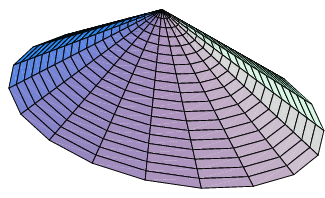
An elliptic paraboloid is of the form:
Such a plane is symmetrical to the planes x = 0 and y = 0.
The only intersect point with the axes is the point O(0, 0, 0).
The plane is either up (c > 0) or down (c < 0) of the plane xy depending on c...
The cross-sections of it with the planes that the axes define in pairs of 2 are:
- x = 0: the parabola z = (c/b^2)y^2
- y = 0: the parabola z = (c/a^2)x^2
- z = 0: the point O(0, 0, 0)
Elliptical cones
A elliptical cone is represented by the equation:
Such a plane is symmetrical to the planes that are defined by the axes in pairs of 2.
The cross-sections of those planes with the cone are:
- x = 0: the lines z = +- (c/b) y
- y = 0: the lines z = +- (c/a) x
- z = 0: the point O(0, 0, 0)
More specifcially the cross-sections of the planes z = z0 of the plane xy with the conical plane are ellipses which centers that correspond to the axis z and vertices parallel to the previous lines.
For a = b we get a right circular cone.
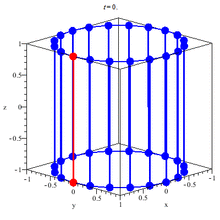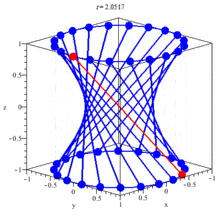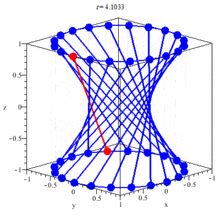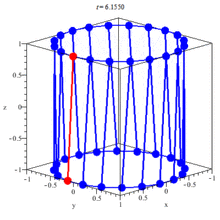
Hyperboloids
Hyperboloids of one cone are of the form:
Which is a plane that is again symmetrical to the planes defined by the axes in pairs of 2.
The cross-sections with this planes are this time:
- x = 0: the hyperbola y^2/b^2 - z^2/c^2 = 1
- y = 0: the hyperbola x^2/a^2 - z^2/c^2 = 1
- z = 0: the ellipse x^2/a^2 + y^2/b^2 = 1
Such a plane is cohesive which means that all the points are connected and so we can go to any point starting from any point.
We can also have double-cone planes that are of the form:
This plane is again symmetrical to the planes defined by the axes in pairs of 2, but it doesn't intersect with the plane z = 0.
But, we still have cross-sections that this time are the hyperbolas:
- x = 0: the hyperbola z^2/c^2 - y^2/b^2 = 1
- y = 0: the hyperbola z^2/c^2 - x^2/a^2 = 1
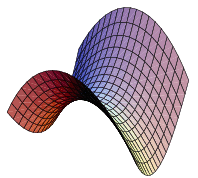
A Hyperbolic Paraboloid
Lastly, let's also talk about hyperbolic paraboloids.
As you can already see we can create any form and shape we wish by tweaking the simplest equation which is the ellipsoid one...
In the same fashion an plane of the form:
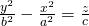 , z > 0 (quicklatex)
, z > 0 (quicklatex)
is a hyperbolic parabola.
Such a plane is symmetrical to the planes x = 0 and y = 0.
The cross-sections with those planes are:
- x = 0: the parabola z = (c / b^2) y^2
- y = 0: the parabola z = -(c / a^2) x^2
In the plane x = 0 the parabola passes through the center of the axes O(0, 0, 0) and "opens upwards".
On the other hand on the plane y = 0 the parabola "opens downwards".
When cutting through using z = z0 we get a hyperbola.
And this is actually it for today and I hope that you enjoyed it.
There is even more to learn about planes and equations that describe them, but I hope that this and the previous post gave you an idea about what those planes are and how they look in space!
Next time we will get into multi-variable and vector functions!
Bye!

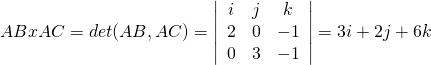
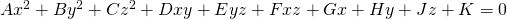
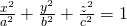
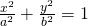
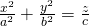
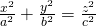
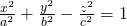
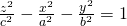
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by drifteritis from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.