Mathematics - Mathematical Analysis Partial Derivatives
Introduction
Hello it's a me again drifter1!
Continuing on with our Mathematical Analysis series of Mathematics we today will talk about Partial Derivatives.
Those "new" derivatives are based on the "normal" ones and so I highly suggest you reading my post about that here before getting into this post...if you don't know about them already!
So, without further do, let's get started!
What does a derivative describe?
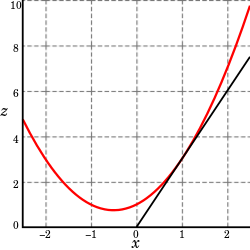
When having only one variabe, the derivative of course describes the angle/rotation of a function's curve to the x axis.
So, the derivative of a function f(x) with x describes the angle towards the x-axis.
But, what about functions of more then one variables?
Well we saw that limits, continuity and more can also be described for such functions, but we don't talked about differentiation yet...
Depending on the notation the derivative at the position xo is given by:
using quicklatex
So, the derivatives are based on an specific quotient limit...
Partial Derivatives
Because we can clearly see that the "dependence" variable (x) is in the denominator we start thinking about a way of describing derivatives for one of the independent input variables. This exactly is what a partial derivative is.
For two variables we define the partial derivative of z = f(x, y) at the point P(x0, y0) with x as:
Wikipedia and Quicklatex
If this limit exists (is a real number) then the value is called the partial derivative o f(x, y) with x at the point P(x0, y0).
By doing as we did, we actually define a new function f(x, y0) that is dependent only of x.
Using the same principle the derivative of f(x, y) with y is:
For example:
The Partial derivatives are:
f'x = 2x + 3y
f'y = -2y + 3x
We can clearly see that the "other" variable is being treated like a constant.
What does the partial derivative describe?
Well, it again describes the angle of a curve...
This curve will be different depending on which variable we choose to derivative with.
For the function f(x, y) at P(x0, y0) we have:
- f'x or the partial derivative with x at P describes the angle of f(x, y0)
- f'y or the partial derivative with y at P describe the angle of f(x0, y)
You can see that we find the angle of a new function g(x) or g(y) which means that we leave the 3-dimensions that a 2-variable functions describes to go to 2-dimensions (from plane to curve/line)
But, how can this be useful?
Derivative of Vector Functions
The derivative of a vector function is based on partial derivatives.
Suppose z = f(x, y) is a plane and r(t) = x(t)i + y(t)j a curve (or vector function) on top of it.
We define a derivative along the curve as:
f'(t) = df/dt = ∂f/∂x * dx/dt + ∂f/∂y * dy/dt
where these elements are:
- the partial derivative of x(t) with x AND
- the partial derivative of y(t) with y
But, because the functions are "complex" we have to use the rule of composition.
If we had 3-dimensions the derivative would look like this:
f'(t) = df/dt = ∂f/∂x * dx/dt + ∂f/∂y * dy/dt + ∂f/∂z* dz/dt
For example if r(t) = cost + sint and f(x, y) = x*y then:
f'(t) = df/dt = ∂f/∂x * dx/dt + ∂f/∂y * dy/dt = y*(-sint) + x*cost = -sin^2t + cos^2t
Partial Derivatives are also used for things like:
- Finding normal vectors to a plane
- Finding tangent planes
Both use directional derivatives that we will talk about next time...
And this is actually it for today and I hope that you enjoyed it!
Bye!
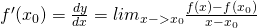
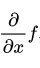
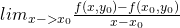
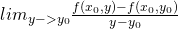
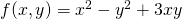
Just have a thing for general mathematics and derivatives because of my career line: am an accountant. Really love your blog @drifter1.
I have love for programming, but it has always seemed to me as one big thing to acquaint with...any help for people like me? [smiles]
Thank you for your kind words...
Programming is interesting and you can create programs/code that can do anything you wish (mostly), but because of this diversity it's difficult to find something easy to start with.
I suggest you to start with something like C.
C is an easy language which has a grammar that is used even in more advanced languages like Java for things that are common.
Start by creating something that just prints out, continue with something that takes your input, does some calculations and gives you an output (or just prints it out) and so on...
It's not so difficult to learn programming anymore!
There are many great sources and videos online :)
Thanks for your timely response. I hope you dont mind sir, because am deviating from the subject matter (derivatives) under which this comment is presented. Is it possible that i can bring myself to a level of relatively great relevance in the programming ecosystem without having any formal (classroom/college based) education in Computer Science? Cos most of the Tech guys i have met in the past always gave me the impression: I cannot be as good...
Haha no problem at all..
Learning computer science through an university will indeed help you a lot, but there are a lot of great programmers that left university or even never got to an university for the topic they are working on!
In an university you don't learn deep knowledge for each topic, but just general knowledge.
This is common for all the different scientific branches and for Computer science which is very wide and has many different topics to work on and where things change day after day very fast, this is of an even greater degree.
No-one is perfect and there always is a way of writing code better, faster, "cheaper" etc.
The thing is: You can learn if you want too.
It might take you more time to get to a level that more professionals are at now, but it's not impossible.
Wish you good luck, just start simple!
[Eureka!!!] At least there is hope for people like us... Thanks @drifter1. It was lovely making an acquaintance with you. FOLLOWING.
very good remind of derivatives, i will follow your courses to understand more mathematics from you and to not forget what i learnt before, and i will be thankful you add some excersises in your posts. thank you very much :)
Sure :)
I'm mostly posting exercises separately and for many things together, just to keep theory and examples better organized...
Today's topic was not so difficult, but for more advanced stuff I of course have more examples or even explain the theory using an characteristic and describing example.
Glad that you enjoy it and remember/learn :D