Mathematics - Mathematical Analysis Multivariable and Vector Functions
Introduction
Hello it's a me again drifter1! Today we continue with my talk about more advanced stuff of Mathematical Analysis by covering different kinds of functions: multi-variablle and vector functions.
In the previous posts we covered Vectors, Lines, Planes and also a lot of Plane Types, and those Planes are of course multi-variable functions...
Anyway, this post will disuss some more things about those multi-variable functions and just to have a little more to talk about we will also give a small introduction of Vector functions, which are another representation of curves (or even planes) in space!
So, without further do, let's get started!
Functions
Let's first start with functions in general (mostly single-variable ones) so that we have a smooth start and so that you remember what you already know about them...
The basis of the whole Mathematical Analysis branch are Functions for which we even talked about in our first post, our introduction to this series that you can find here.
There I cover a lot that can be very useful, but here a small recap...
A function f from a non-zero set A to a non-zero set B is a rule f, that corresponds each element x of set A to only one specific element y of set B. We symbolize it as f: A -> B. We say that "f is a function from A to B".
Some more things:
- x is the independent variable and y is the dependent variable or image of x (y = f(x))
- A is the domain of definition and B is the domain of range
ATTENTION:
A function can have multiple x's that go to the same y (think about f(x) = c, where c is a constant), but a function can not have multiple y's that go to the same x (or x's can not go to two or more different y's).
Some functions are:
- f(x) = x^3 + 5
- g(x) = 98
- h(x) = 5/x
You can read about the rest in the introduction, cause that is enough for today's topic...
Dual-variable Functions
In reality most things are dependent of more then one things...
As we know from Physics, Force is:
F = ma
and so dependent of two variables m and a!
Another great example is:
V = πr^2h
that gives us the volume of a spherical cylinder dependent of it's radius (r) and height (h) multiplied by the constant π.
Also check out this.
So, what changes when we add one more variable into a function?
- The domain of definition now is a set of ordered pairs s (x, y)
- The domain of range f(x, y) is a set of real numbers like it was before
The definition of a dual-variable function looks like this:
Suppose D being the set of ordered pairs of real numbers (x, y).
A real function f of two variables is a rule that corresponds one specific real number:
w = f(x , y)
for each ordered pair (x, y) of D.
D is called the domain of definition of f and the set of values that w gets is called the domain of range.
The independent variables x and y are also called input variables.
The dependent variable w is called a output variable.
So, because of that definition the example's equation can also be written like this:
V = f(r, h)
so that the independent and dependent variables are better distinguished.
Domain of definition
So, how do we find this set?
We use the exact same method as in single-variable functions by excluding things that cannot be defined like negative roots (complex numbers) and divisions with zero.
For f(x, y) = root(y - x^2) we of course have:
D = [0, ∞)
which can be found from:
y - x^2 >=0 => y >= x^2 and so y >= 0
Bounds
In the same way as single-variable functons where bounded we again define something like that for more than one variables.
A "set" of a Plane is bounded if it can be surrounded by a circle of finite radius.
Else we say that it is not bounded...
Some more things:
- A point (x0, y0) of a set R of plane xy is an internal point of R if it is the center of a circle that is totally a part of R.
- A point where each circle drawn of it as a center contains the same amount of points inside and outside of R is called a boundary point.
The set of all internal points define the internal space of a space.
A set is open when it contains only the internal points and closed if it contains only boundary points.
Functions of 3 or more variables
Some functions may also be dependent of 3 or even more variables!
For 3 variables we can continue with what we said previously by saying that:
A function f of 3 or even more variables is a rule that corresponds each ordered trio (x, y, z) of domain of definition D to one only real number w = f(x, y, z).
The domain of range of course contains all the real values of the output variable w.
So, generalizing for n-variables we get:
A function of of n-variables is a rule that corresponds to each n-pair of real numbers (x1, x2, ..., xn) one real number w = f(x1, x2, ..., xn).
The variables x1, x2, ..., xn are the independent input variables.
The variable w is the dependent output variable.
We can again define things like before, but I will skip it for simplicity...
Plotting those functions
A function of 1 variable can be plotted very easily in 2-dimensional space.
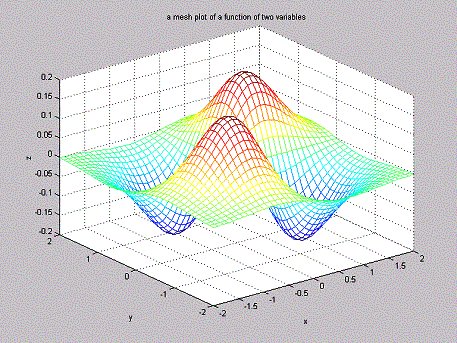
A function of 2 variables is plotted in 3-dimensional space and so can be represented visually.
But what about the others?
We can't represent and understand those functions of 3 or more variables in a way that is more close to us, but there are many strong theorems and tools that help us understand them and use them in mathematical, physics, chemistry etc. problems.
Limit and Continuity of multi-variable Functions
The limit doesn't change that much...
We define the limit of a 2-variable function like that:
lim (x,y) -> (x0, y0) [f(x, y)] = L
And so each variable tents to a value!
We again can define one-sided limits and so the limit only exists when:
- The limit is finite (not infinity, but a real number)
- The one-sided limits have the same exact value
For the continuity not much changes again and so a function f(x, y) is continuous at the point (x0, y0) when:
- f can be defined at (x0, y0)
- the limit at that point exists AND
- lim (x, y) -> (x0, y0) [f(x, y)] = f(x0, y0)
A function is continuous when this is true for all the points!
The same exact stuff can also be said for 3 or more variables...
Derivatives, Integrals etc. will be discussed separately in other posts later on...
Vector functions
So, after talking about multi-variable functions we can now also get into another form of function, which are the vector functions...
Curves in space are defined by functions for each coordinate in this space in a specific "period" I of time so that:
x = f(t), y = g(t) and z = h(t) with t in I
The functions/equations x, y, z are parameters of this curve.
So, those points (x, y, z) = (f(t), g(t), h(t)) compose the curve of an "object" if we think of this curve as the motion of an object...
Another way of representing that is by using a vector:
r(t) = OP = f(t)i + g(t)j + h(t)k
where O is the center of the axes and P is the final destination P(f(t), g(t), h(t)).
The function f, g, h are called component functions of the position vector r.
So, what is r(t)?
r(t) is the vector function of the real variable t in the interval I.
Generalizing it even more we can say that:
A vector function (function with vector values) with a domain of definition D is a rule that corresponds a vector in space for each element of D.
For the time being the vector functions define only curves, but later on (other posts) we will see that we can also define planes!
An example:
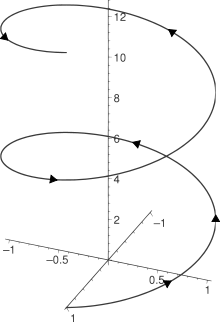
r(t) = cos(t)i + sin(t)j + tk
This function can desribe a Helix shape like this one:
What about limits and continuity?
Well, the limit will equal to the limit of each "part" and so:
lim t->t0 [r(t)] = lim t->t0 [f(t)] i + lim t->t0 [g(t)] j + lim t->t0 [h(t)] k
Such a function will be continuous at the point t = t0 when:
lim t->t0 [r(t)] = r(t0)
When that happens for all the points of D then the function is continuous!
We will talk about derivatives and more stuff another time..
And so this is it for today and I hope that you enjoyed it!
Next time we will get into differentiation/derivatives of this types of functions!
Bye!

Followed you @drifter1. It's a great pleasure to have this kind of content in steemit space. Keep writing. I'm also a Maths + Tech lover
good job, i will wait your post about differentiation/derivatives :)
Good post!