The Birthday Paradox and Our Awful Human Intuitions When It Comes to Probabilities and Exponents
Here's the riddle: you have a room full of people and you want to find two people who share a birthday. The question is how many people do you need to get in there so you would have at least a 50% chance of success. How about 75%? And how about 90%?
How about a chance higher than 99%? Don't try to figure it out with math and statistics, give me a ballpark figure off the top of your head! And if you are familiar with the problem, feel free to skip ahead to the more advanced version at the end.
You are going to need one hell of a room, right? Well, if you trust your human intuition (and you haven't heard of this type of problem before), you most likely gave an answer that was seriously off. This is because our brains were never made for solving problems like this intuitively.
Well, let's figure it out!
Disclaimer for the super-pedantic: For the sake of this problem we'll assume that a person has an equal probability to be born on any day of the year and we'll ignore leap years and birthdays falling on the February 29 and disregarding all actual data of people being more often this or that month. We don't want to get bogged in minutia, we want examine how different probabilities work, so we'll concentrate on that.
The Answers
Let me tell you, people wouldn't be calling this a paradox or a problem if the answer was something expected. If any of your guesses were over 100 (even of the 99% one!), you guess was way too high!
Be honest, was your guess for 50% higher than 57 people?
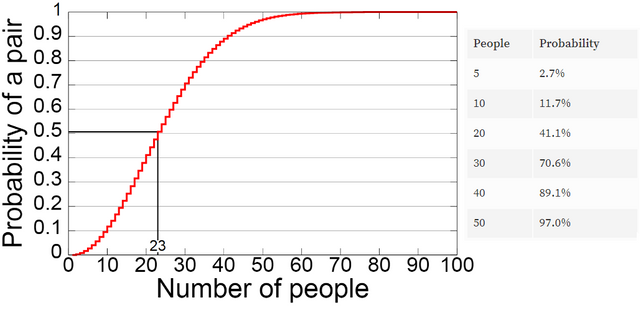
Just 23 people are a sufficiently high sample that if you did this 10 times in a row, you would most probably get matching birthdays 5 times. The chance of a match is one in two. And the probability of a match increases significantly with every additional person added to the room. Dial it up to 57 people in the room and you are practically guaranteed to have at least two people with matching birthdays. At that odds you can try it 10 times in a row with a new batch of 57 random people and your chance of getting a pair 10 times in a row would be over 90%.
But let's try to understand why so few people are enough for such high odds.
Understanding How This Is Calculated
Let's take the situation when we have 23 people in the room just like I've shown in my professional illustration with the stick figures and the birthday cake. We have two people with the same birthday and those are the guys with the party hats on. The easiest way to calculate the odds of this happening are to start by figuring out the probability of this not happening. As the outcome is binary (there will either be at least one match or there will be no match at all), the two probabilities need to add up to 1 which is 100% or one in one chance.
The chance for the first person to not get a match is 100% or 365 out of 365. There is a total of 365 birthdays and birthday they pick would not have been taken. The chance for the second person picking a birthday that has not been taken yet is 364 out of 365 as there is one birthday that would yield a match. Then the probability of the third person is 363 out of 365 as we need to exclude both birthdays that are already taken.
In that way every next person has a slightly lower chance of picking a unique birthday as free options gets smaller by one every time. And since all of those events need to happen we need to multiply all the probabilities together. For 23 people it looks like something like that:
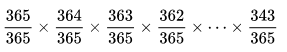
This gives us:
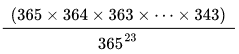
Doing the calculation gives us about 49.3% chance of not having any matches. This means that the probability of having at least 2 birthday matches is about 50.7%.
We can generalize this calculation and use one formula to determine the chances of having at least one match for any number of people we might have in the room. If we mark the number of people with n, the resulting formula would be:
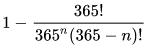
When we apply this calculation to all possible numbers of people we can have we can see how the probability of a match increases exponentially much faster that we could intuitively expect which is evident in the graph below.
We can clearly see that the chances for a match start increasing exponentially and they start approaching 100% so rapidly that at that scale we can only plot them on as 100% and the red line is at a probability of 1.
An Easier to Grasp Approximation
If you want to think about the case when we have 23 people and try to understand why the probability of a match is so high, you could look at a bit of simpler calculation that can still give is a ballpark figure. We can look at the chance of a single pair to have birthdays that don't match. It will happen most of the time and the chances would be quite high - 364 to 365 which translates to 99.73%.
But when we have 23 people in the room, all the possible permutations of pairs to compare is 253. When we have just a few pairs to test 99.7% means the chances to have a mismatch between the birthdays is quite high. But if you keep testing that over and over, the otherwise minuscule chance of a match starts growing exponentially.
To get the ballpark figure, you can multiply the probability for a single pair mismatch as many times as there are pairs. This means you need to calculate (354/356)253 or 99.73%253. And even a high probability tested a lot starts dropping fast and using this calculation we get the chance of no match at 23 people to be about 49.95% which leaves is with 50.05% as our ballpark chance of a match with 23 people in the room.
I keep using ballpark here because this calculation examines pairs if they are isolated evens when they aren't and this gives a bit lower probability of a match than the more accurate calculation presented above, but this might be easier to understand especially to the not so mathematically inclined.
Why Is This a Paradox?
As many other things that we sometimes call paradoxes, there is no real paradox here. This calculation describes the way the world around us works accurately and the real problem here is the way our primitive ape brains function. If it sounds counter-intuitive, the flaw lies with our intuition, not with the math. Everything here is logical and makes perfect mathematical sense. This is why many people call this The Birthday Problem as it is not really a true paradox.
So let's see what exactly in our psychology misleads us.
We Think Egotistically
When we are asked a question like that, we tend to imagine things from the perspective of a single participant. Just like we do with movies, it's hard for us to actively empathize with everybody in the group at the same time and we tend to imagine things better when we look at them from the point of view of a single person. But when we do that, we are subtly changing the question. The question is about the chance of any two people in the room having the same birthday but we subconsciously paraphrase it to the chance of another person in the room having the same birthday as ourselves.
In the case of 23 people in the room, when thinking that way our mind examines 22 chances of a match - us against the other 22 people. But this self-centered outlook on the situation ignores the fact that all the other possible pairs in the room give us a chance for a match. When we have 23 people in the room, there are 253 unique pairs of people with each one yielding us another chance at having a match. Thus when we allow our intuition to lead us into thinking about the problem from the point of view of a single person, we tend to significantly underestimate the odds as we are examining 22 chances instead of 253.
We Think Linearly
The type of calculation that is needed for calculating probabilities is simply not the type of of calculation our head is good at. We are relatively good with linear progressions like adding the same value over and over. But as soon as we exponents start factoring into the equation, our mathematical intuitions usually break down. Some goes for multiplying fractions many times over. And as probabilities are fractions with a tendencies for exponential growth or decline, it's really hard for us to wrap our brains around that.
To put it simply even minuscule chances make a difference if tested over and over. When we have an event that is quite unlikely like two people having the same birthday and take that chance over and over, we end up with a probability that is actually high. The chance of two people having the same birthday is really small, but when you test that chance 253 times it starts growing exponentially. And since the initial chance is so small that our brains can't really approximate it properly, we simply don't have the computational power or understanding to track the way it will grow in our heads.
A Modified and More Difficult Version of The Problem
So now that we know that our intuitions are flawed and when we've seen how the probabilities behave in this scenario, do you think you would be able to make a better guess if we tweak the parameters in a new way.
Let's look at the same problem, but this time we want at least 3 people sharing the same birthday instead of 2. That's obviously much less likely, but by how much? How many people would you need for a 50% probability and how many people would you need for a 90% probability? What would the probability of getting 3 people would the same birthday be when you have 23 people? How about 50, 80 or 100?
Can you make a good guess without doing the math? Let's see...
The Sets of Probabilities Side by Side
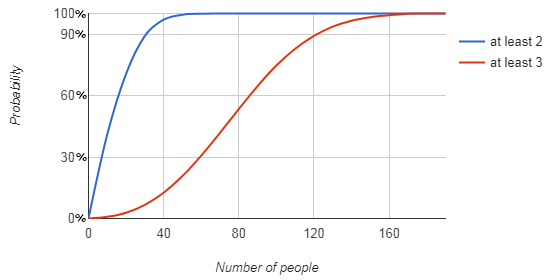
| Number of people | Probability (at least 2 people) | Probability (at least 3 people) |
|---|---|---|
| 20 | 41.1% | 0.8% |
| 30 | 70.6% | 2.8% |
| 40 | 89.1% | 6.7% |
| 50 | 97.0% | 12.6% |
| 60 | 99.4% | 20.7% |
| 70 | 99.9% | 30.7% |
| 80 | ≈ 100% | 41.8% |
| 90 | ≈ 100% | 53.4% |
| 100 | ≈ 100% | 64.6% |
| 110 | ≈ 100% | 74.6% |
| 120 | ≈ 100% | 82.8% |
| 130 | ≈ 100% | 89.1% |
| 140 | ≈ 100% | 93.6% |

Sources:
- https://betterexplained.com/articles/understanding-the-birthday-paradox/
- www.wolframalpha.com/input/?i=birthday+problem+23
- https://en.wikipedia.org/wiki/Birthday_problem
Images without cited sources are original work or modified CC0




Being A SteemStem Member
Very good article Dave! Probabilities and statistics are indeed highly nonintuitive, i think that's part of the problem when it comes to communicating scientific data to the public.
The Monty Hall problem is another cool example that took me a while to wrap my head around:
https://en.wikipedia.org/wiki/Monty_Hall_problem
Thank you, Carl, I'm happy you think so! You are absolutely right about science communication.
The Monty Hall problem is a great example of that indeed and I was thinking about mentioning it in this post along a few coin toss example, but the post was already getting quite long and I decided I'll maybe write about them in the future.
@carlgbush: ....uh... what? Which data? Ah, you mean: NUMBERS?
Well, totally lost on me ;-) I tried really hard all my life. But never came near any kind of enthusiastic feeling about crunching numbers. ...Wait, there was a day when I was practicing maths with my son and I looked up the Internet for Chinese calculating. That got me hooked for quite a while. But it was for 3d graders. LOL
All my teacher's fault - If @rocking-dave would have taught me, I guess, I would be now Superwoman. HaHa!
Well I have to say I'm pretty amazed. I thought at least a few hundred people.....and we think it such a coincidence when we meet someone with the same birthday as ourselves. Primitive ape brain indeed.
I did try to follow the maths but my head hurt, ......but I trust you.
Thank you for stopping by yet again and for your continued support throughout this month-long challenge! You were a part of the inspiration to try it and a big part of staying motivated enough to (almost) succeed at it! :)
And thank you for bearing with the math parts! :D
I remember that when I first met this little problem, I though I was really smart to get my ballpark by dividing 365 by 4 (2 for 50% and 2 because it was pairs) which meant somewhere in the 90-100 range. I was blown away when I realized my ballpark figure was still about 4 times too big.
I was really conflicted about how much actual math I should include in the post. I tried to keep it to a minimum without skipping it completely and I was actually considering replacing some of it with "trust me, this is how the math works out". ;) I guess the hardest thing about a post like that is to decide at what level of math understanding you should aim it at. I have no clue if I was anywhere close to a good balance on that.
In your opinion, was the math too much? Would the post have been more effective or lest boring and/or tiring if it included just some of the results and a shorter explanation on how they were derived?
No, I don't think you included too much maths at all. It's a genuinely interesting article and I'm sure many love to see how it all works out, it's just I've never had much of a head for it.....dunderhead I think my maths teacher used to call me.
Such a diverse range of subjects you cover. I dunno where you get the ideas from!
Thank you for the feedback! :)
I guess the diverse range of subjects I cover comes from the diverse range of interests I have. I've shared before how consistency is something really hard for me in general, but this is not just about my work rate, it also translates into my attention span and my interests which are also all over the place.
Well for a man who finds consistency a challenge, you're not doin' too badly atall atall. And when it comes to blogging, I guess your interests being all over the place is something of an advantage. I'm certainly learning a few weird and wonderful facts. If it weren't for you I'd still be trying to get rid of the phloem every time I peel a banana;)
It helps, not doubt! :)
Hahaha, I can't believe someone actually remembers that phloem post! It was my most spontaneous one ever on this platform.
Remember it? Sure I'll never forget it!
That warms my heart actually! :) It really means a lot to hear! Talk about motivating and encouraging things to read in a comment!
I love this little paradox! There's such a human ineptitude for not just mathematical reasoning, but for all forms of logic which don't follow a simple patter (black vs white, a+b=c, y=ax etc...).
I think fighting against this tendancy is what makes being a scientists or taking an active interest in science so great. Physics doesn't follow a 'logical' set of rules. Evolution doesn't take the path of least resistance. Metabolism does not work the most direct or efficient way. Nowhere in the natural world do we see things working the way that our mind would have designed them to work!
Awesome read, thanks :)
You are right, all very good examples. Counter-intuitive things are the ones that fascinate me the most and I personally find them to be the most interesting types of results.
Thanks for stopping by and giving a bit of an older post a read :)
Always looking for good reads :P
I had two people in mind at the 50% one. I mean, there's a 50% chance they both share the same birthday...
At least, now that I think about it, that's complete bogus...
Yeah, the chance of two random people sharing a birthday is under 0.3%.
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by rocking-dave from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Good i need your esteemed help i am new in this esteem
This is not the way to go, what you're doing is comment spam and if you keep it up, you'll start getting flagged.