ESTUDIO DE LA SENSIBILIDAD DE LA RESPUESTA DE UNA ESTRUCTURA PARA DISTINTOS CASOS DE FRACCIÓN DE AMORTIGUAMIENTO CRÍTICO “ξ” EN BASE A LA DURACIÓN DE LA EXCITACIÓN EXTERNA. APLICACIONES EN LA INGENIERÍA SISMORESISTENTE

INTRODUCCIÓN

La duración de la excitación dinámica externa “p(t)” que experimenta una estructura, es un aspecto de importancia a considerar en el desempeño que esta pueda tener ante este tipo de solicitaciones, entre las que destacan las producidas por un sismo. Sin embargo, es importante lograr afianzar conceptos bases en la dinámica estructural, idealizando la excitación externa como una vibración forzada armónica; en base a esta premisa, en la referencia N°04, realicé un estudio sobre las amplificaciones dinámicas máximas que alcanza una estructura sometida a una fuerza armónica, para distintos valores de fracción de amortiguamiento crítico “ξ”, en el caso de que la frecuencia de la excitación externa “ω” se iguale con la frecuencia natural “ωn”, lo que se podría catalogar como “resonancia”; se demostró en dicho artículo, la existencia de una relación inversa proporcional entre el valor de la fracción de amortiguamiento crítico “ξ” y el desplazamiento máximo dinámico “uo” que se alcanza. Ahora bien, tomando como base el mismo sistema estructural de la referencia N°04, con ayuda de modelos teóricos y de la herramienta computacional NONLIN V 7.14, estudiaremos en este artículo la sensibilidad de la respuesta de la estructura, en cuanto a la cantidad de ciclos que esta requiere para alcanzar el tope de deformación dinámica máxima “uo”, donde influye directamente el tiempo de duración de la excitación externa “p(t)” y la condición de fracción de amortiguamiento crítico “ξ” de la estructura en cuestión.

Imagen N° 01: una visión general de la temática a estudiar

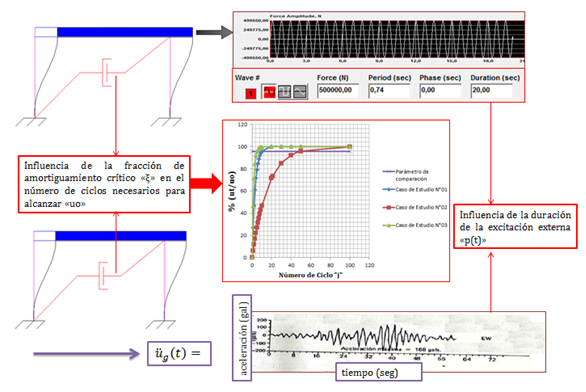
Fuente: Sauter (1989), Chopra (2014), NONLIN V 7.14, adaptada por Santana (2018)

Una vez desarrolladas las aplicaciones prácticas que nos permitan afianzar las ideas citadas anteriormente, donde la excitación externa “p(t)” está representada por una fuerza armónica (ver imagen N°01), extrapolaremos estos principios al campo de la ingeniería sismoresistente, donde la excitación externa es aplicada en la base de la estructura, y su función está representada por un acelerograma, reflexionando especialmente en este trabajo sobre los sismos de larga duración, y los efectos catastróficos que estos han originado en las estructuras, para lo cual tomaremos como referencia el terremoto de México de 1985, cuya duración fue mayor a los 60 segundos. En la imagen N°01 se ilustran estas ideas.

DELIMITACIÓN DE LA TEMÁTICA A ESTUDIAR

En aras de mantener una sincronización en la profundización de las ideas expuestas en la referencia N°04, la estructura modelo tiene las mismas características, entre las que destacan que se trata de un pórtico plano con un grado de libertad tanto estático como dinámico.

Imagen N°02: estructura en estudio

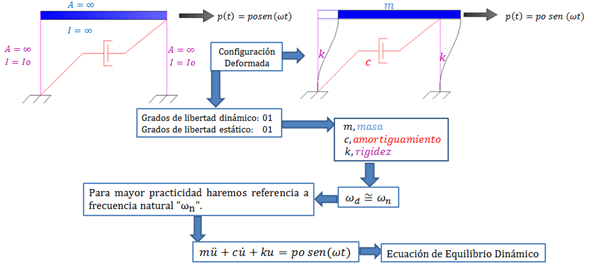
Fuente: Santana (2018)

El pórtico en cuestión está sometido a una excitación armónica de frecuencia “ω” representada por la fuerza “p(t)”; nos enfocaremos en este estudio en la condición de resonancia, producida cuando la frecuencia anteriormente descrita iguala a la frecuencia natural “ωn” o frecuencia amortiguada “ωd”, las cuales se demostró en la referencia N°05, tienden al mismo valor, por lo que para fines prácticos, hablaremos simplemente de frecuencia natural “ωn”.

Es importante señalar, que en este caso de resonancia con presencia de amortiguamiento en el sistema estructural que se analiza, los desplazamientos dinámicos no tienden al infinito, como ocurría en el caso de resonancia sin amortiguamiento (ver. ref. 07), sino que estarán restringidos en base a la ecuación N°01, en la que la fracción de amortiguamiento crítico “ξ” que se define es trascendental para este aspecto. Previo a profundizar sobre la influencia de la duración de la excitación externa “p(t)”, lo cual realizaremos con ayuda de la herramienta computacional NONLIN V 7.14, abordemos en primera instancia, la cantidad de ciclos que tiene que experimentar la estructura para alcanzar un nivel dado de deformación dinámica “u(t)”.

ABORDAJE MATEMÁTICO PARA LA ESTIMACIÓN DE LA CANTIDAD DE CICLOS DE UNA ESTRUCTURA PARA ALCANZAR LAS MÁXIMAS DEFORMACIONES DINÁMICAS

La cantidad de ciclos que debe experimentar una estructura está influenciada grandemente por la fracción de amortiguamiento crítico “ξ” de la misma, tomando valores para el caso de los sistemas sub-amortiguados de interés en la ingeniería sismoresistente “ξ<0.10”, tal como lo señala Chopra (2014). Basados en lo expuesto en el tópico anterior, al producirse la condición de resonancia, la respuesta en términos de desplazamiento dinámico “u(t)” del sistema estructural que se analiza, obtenida a partir de la solución de la ecuación diferencial de equilibrio dinámico (ver ref. 04), es la siguiente:

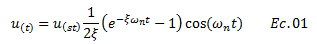
La ecuación N°01 puede ser rescrita tomando en consideración los siguientes aspectos:

a.- La relación fundamental para el cálculo de periodo natural “Tn” en función de la frecuencia natural “ωn”:

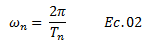
b.- Asociando el tiempo “t” en el cual se evalúa la respuesta dinámica en términos de desplazamiento con el periodo natural “Tn”, a través del número de ciclos:

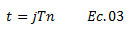
Dónde:

j, hace referencia al número de ciclos.

Dado que el periodo es el tiempo que requiere la estructura para completar un ciclo, al multiplicarlo por el número de ciclos “j” nos daría el tiempo “t” en el cual podemos evaluar la respuesta de la estructura que se analiza.

Procedamos a sustituir las ecuaciones N°02 y N°03 en la ecuación N°01 de la siguiente manera:

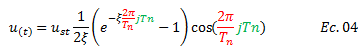
Rescribimos:

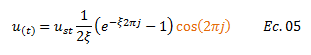
Partiendo de la expresión que define el desplazamiento máximo dinámico “uo” que el sistema estructural puede alcanzar para el caso en el cual la frecuencia de la excitación externa “ω” coincide con la frecuencia natural “ωn”:

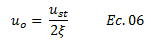
Se despeja el desplazamiento máximo estático “ust” de la forma:

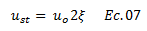
Sustituimos la ecuación N °07 en la N°05:

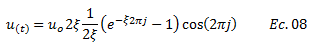
Rescribimos la ecuación N°08:

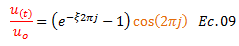
El término resaltado en color “rojo” de la ecuación N°09, se puede interpretar como el nivel de desplazamiento dinámico que se ha alcanzado para un instante de tiempo “ut” con respecto al desplazamiento dinámico máximo “uo” que el sistema estructural puede experimentar. Una variable de importancia en la ecuación N°09 es la cantidad de ciclos “j” a evaluar. Resaltando que esta variable tomará números enteros. En este sentido conviene analizar el término resaltado en color “naranja” de la ecuación N°09, para distintos valores de “j”:

Tabla N°01: influencia de “j” en el resultado de “cos (2πj)”

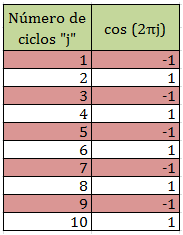
Fuente: Santana (2018)

Se demuestra que para ciclos impares el término resaltado en color “rojo” de la ecuación N°09, toma valores negativos. Sin embargo para los fines de este artículo, conviene expresarlo en valor absoluto, para facilitar la interpretación gráfica de la sensibilidad de la respuesta de la estructura para distintos valores de fracción de amortiguamiento crítico “ξ”, para el caso de que la frecuencia externa “ω” iguala a la frecuencia natural “ωn”. Por lo tanto la ecuación N°09, la podemos presentar así:

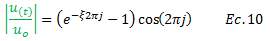
Si el término de la ecuación N°10, resultase igual a la unidad, para una determinada cantidad de ciclos “j” y fracción de amortiguamiento crítico “ξ”, es un indicativo que se ha llegado a la máxima deformación dinámica “uo”, producto de la condición de resonancia “coincidencia de frecuencias”. Por su parte, si el término resaltado en color “verde” arroja por ejemplo un valor de “0.50”, significa que para una cantidad de ciclos “j” y fracción de amortiguamiento crítico “ξ” para la que fue evaluada la ecuación N°10, la deformación dinámica “ut” ha alcanzado apenas la mitad de la deformación dinámica máxima “uo”. Estos planeamientos sugieren que se puede hablar en términos porcentuales, por lo que resultado de la ecuación N°10 se multiplica por “100” para expresarlo de esta manera.

EVALUACIÓN DE LA RESPUESTA ESTRUCTURAL TOMANDO COMO REFERENCIA LA ECUACIÓN N°10

Con ayuda de la herramienta computacional “Microsoft Excel 2013”, se ingresa la función representada por la ecuación N°10, y la misma es evaluada para distintos casos de fracción de amortiguamiento crítico “ξ”, resultados que se aprecian en las tablas N°02, N°03 y N°04, representativas al mismo tiempo de los tres casos de estudios con los que estaremos desarrollando aplicaciones prácticas en la herramienta computacional NONLIN V 7.14.

En lo referente al caso N°01, se tiene:

Tabla N°02: caso N°01, fracción de amortiguamiento crítico “ξ=0.05”. Condición de Resonancia

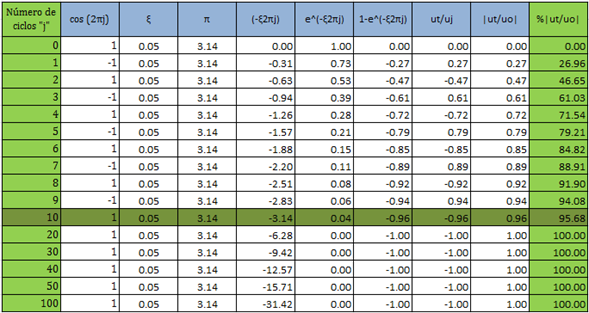
Fuente: Microsoft Excel (2013) adaptada por Santana (2018)

Con respecto al caso N°02:

Tabla N°03: caso de estudio N°02, fracción de amortiguamiento crítico “ξ=0.01”. Condición de Resonancia

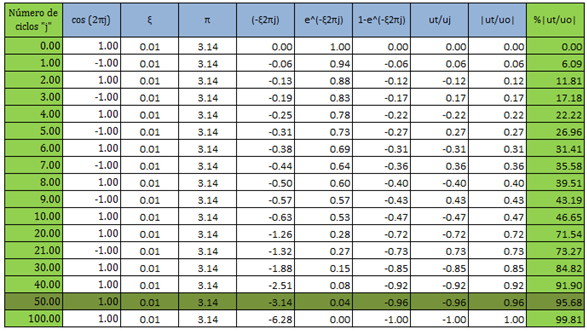
Fuente: Microsoft Excel (2013) adaptada por Santana (2018)

Para el tercer caso de estudio se tiene:

Tabla N°04: caso de estudio N°03, fracción de amortiguamiento crítico “ξ=0.10”. Condición de Resonancia

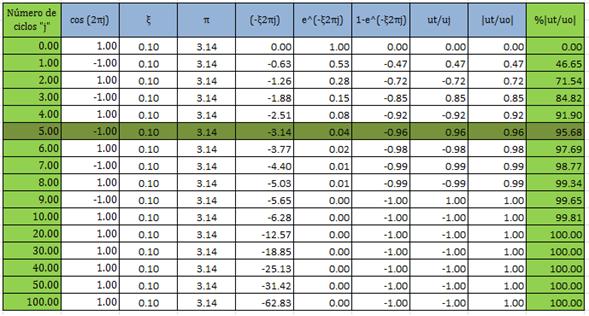
Fuente: Microsoft Excel (2013) adaptada por Santana (2018)

Al graficar los valores de “% |ut/uo|” con respecto al número de ciclos “j”, para cada uno de los casos de estudios, obtenemos el grafico de la imagen N°03:

Imagen N°03: ciclos requeridos en cada caso de estudio para alcanzar la respuesta dinámica máxima “uo

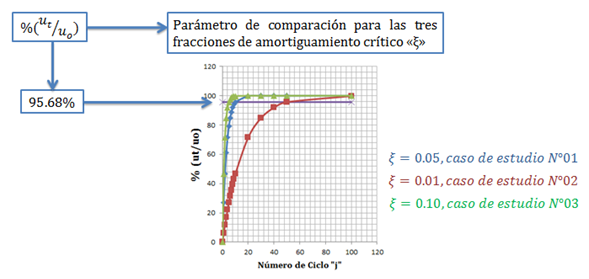
Fuente: Microsoft Excel (2013) adaptada por Santana (2018)

Se aprecia con la ayuda de estos modelos teóricos, la forma como la fracción de amortiguamiento crítico “ξ” es determinante en la cantidad de ciclos a desarrollar para que la estructura alcance el tope de deformación dinámica máxima “uo”. Es conveniente aclarar, que la deformación dinámica máxima “uo” varía para cada fracción de amortiguamiento crítico “ξ”, y esto se ilustra en la imagen N°04, tomando como referencia la ecuación N°06:

Imagen N°04: deformaciones dinámicas máximas “uo” para distintas fracciones de amortiguamiento crítico “ξ”

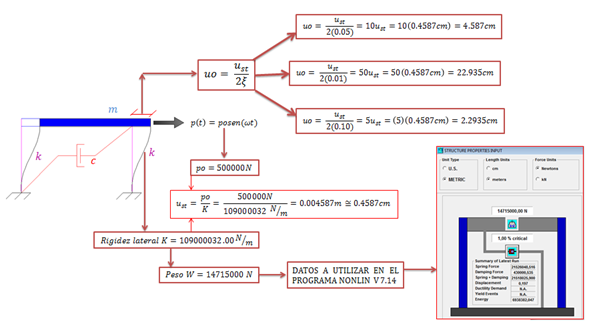
Fuente: NONLIN V 7.14, adaptada por Santana (2018)

Se tiene por lo tanto que para un sistema estructural con una fracción de amortiguamiento crítico “ξ” de “0.05” en condición de resonancia, alcance el 95.68% de “uo=4.587cm” requiere diez ciclos. Por su parte, para el caso de un sistema estructural con “ξ=0.01” en condición de resonancia alcance el 95.68% de “uo=22.935 cm” requiere un total de cincuenta ciclos. Finalmente un sistema estructural con “ξ=0.10” en condición de resonancia, para alcanzar su “uo=2.2935cm” requiere cinco ciclos. De estos análisis, se desprende la influencia del tiempo de duración de la excitación externa, dado que en el caso más crítico que es para un “ξ=0.01” si la excitación externa es de pocos segundos de duración, evidentemente no se desarrollarán tantos ciclos, lo cual influye positivamente en la disminución del riesgo de colapso de la estructura, pese a que se encuentra en condición de resonancia. Profundicemos en la variable tiempo con ayuda de la herramienta computacional NONLIN V 7.14.

DESARROLLO DE MODELO EXPERIMENTAL CON LA HERRAMIENTA COMPUTACIONAL NONLIN V 7. 14

En este programa empezaremos a estudiar la influencia del tiempo de duración de la excitación externa “p(t)”, provocada por una fuerza armónica. Tomaremos como referencia los casos planteados en el tópico anterior. En la imagen N°04 se aprecian los datos principales en cuanto a rigidez “K” y peso “W” que se incluyen en el programa NONLIN V 7.14 y que definen el modelo estructural a evaluar en el programa en cuestión. En la referencia N°04 se hace una ilustración de estos pasos. Y dado que estamos trabajando con los mismos datos, en esta oportunidad, centraré mi atención en las respuestas dinámicas en términos de desplazamientos en el tiempo de la estructura que se analiza, para un determinado tiempo de duración de la excitación externa “p(t)”; observemos las características de esta última:

Imagen N°05: propiedades de la fuerza armónica externa “p(t)”

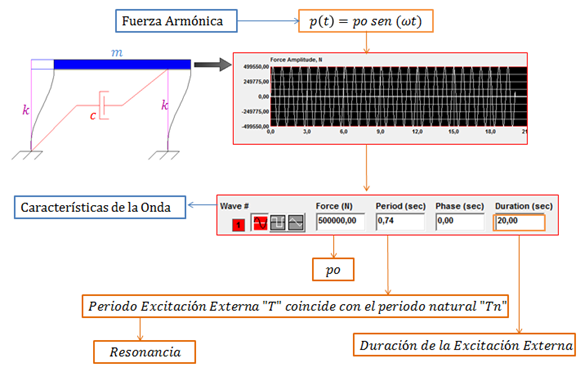
Fuente: NONLIN V 7.14, adaptada por Santana (2018)

Procedamos a estudiar ahora la respuesta en el tiempo de la estructura para los distintos casos de fracción de amortiguamiento crítico “ξ”, lo cual se ilustra en las siguientes imágenes:

Imagen N°06: caso de estudio N°01, ξ=0.05. Condición de Resonancia

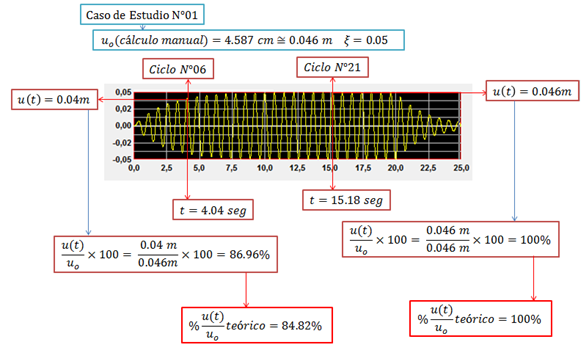
Fuente: NONLIN V 7.14 adaptada por Santana (2018)

Para este caso de estudio, en el tiempo de 4.04 segundos, la estructura ha experimentado seis ciclos, y ha alcanzado el 86.96% de su desplazamiento máximo dinámico “uo”, y ya para el tiempo de 15.18 segundos ha experimentado 21 ciclos, y ha alcanzado el 100% de dicho desplazamiento “uo”. Por lo que se concluye, que a pesar de que la duración de la excitación externa es de 20 segundos, la condición de resonancia permite desarrollar las amplificaciones dinámicas máximas esperadas (ver tabla N°02). Un aspecto que conviene también resaltar, es que las proporciones de desplazamiento dinámicas teóricas resaltadas en el recuadro de color “rojo” de la imagen N°06, hacen ver la precisión del modelo teórico desarrollado en la tabla N°02 y cuya representación gráfica se puede observar en la imagen N°03.

Se aprecia también en el gráfico de la imagen N°06, que el sistema disminuye sus amplitudes, una vez finalizada la influencia de la excitación externa “p(t)”, es decir, un comportamiento típico de una vibración libre amortiguada (ver ref. 05), que sugiere que el sistema recupera su posición original. Vale destacar, que esto hecho se acepta, porque estamos trabajando con la hipótesis de que le estructura se comporta elásticamente, a los fines de afianzar conceptos de importancia en la dinámica estructural. No obstante la realidad indica, que para este estado de resonancia, por ejemplo para el caso de que la excitación externa esté representada por un sismo, las estructuras presentan daños que la alejan de su comportamiento elástico. En la referencia N°06 profundizo en el amortiguamiento más allá del rango elástico.

En lo que respecta al caso de estudio N°02 se tiene:

Imagen N°07: caso de estudio N°02, ξ=0.01. Condición de Resonancia

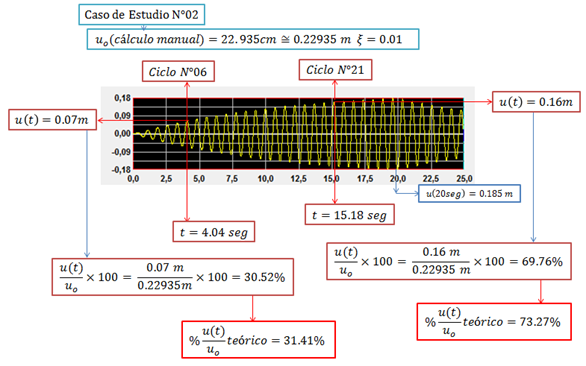
Fuente: NONLIN V 7.14 adaptada por Santana (2018)

En este caso, el sistema estructural presenta una fracción de amortiguamiento crítica “ξ” muy baja, cercana a una condición de resonancia sin amortiguamiento. Notemos que para el tiempo de 4.04 segundos (ciclo N°06), se ha alcanzado el 30.52% del desplazamiento máximo dinámico “uo”, y para el tiempo de 15.18 segundos (ciclo N°21), se ha alcanzado el 69.76% de “uo”.

Este hecho hace ver la importancia de la fracción de amortiguamiento crítico “ξ”, en el sentido de que la estructura requiere una mayor cantidad de ciclos para alcanzar “uo” en relación al caso anterior; esto nos da la idea de que la duración de la excitación externa debe ser mayor. Evaluando el desplazamiento dinámico a los 20 segundos “u(20seg)”, que es el tiempo donde finaliza la excitación externa, su valor corresponde a:

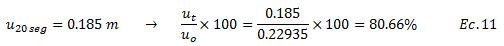
Evidentemente, para este tiempo de “20 seg”, los desplazamientos dinámicos son considerables, provocando una amplificación dinámica en el orden de:

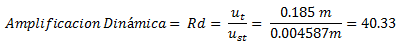
Una gran amplificación que incrementa sustancialmente las probabilidades de colapso de una estructura una vez esta supera el límite elástico, como ocurre en el campo de interés de la ingeniería sismoresistente. No obstante, para los alcances de este artículo, estamos considerando que el sistema se encuentra en el rango de comportamiento elástico, y al cesar la excitación externa “p(t)”, la amplitud de deformación comienza a disminuir, requiriendo este sistema estructural más tiempo, para retomar el estado de reposo, en comparación con el caso de estudio N°01.

En lo que respecta al caso de estudio N°03, tenemos lo siguiente:

Imagen N°08: caso de estudio N°03, ξ=0.10. Condición de Resonancia

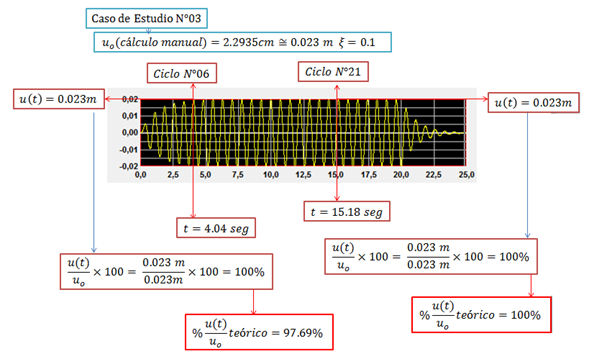
Fuente: NONLIN V 7.14 adaptada por Santana (2018)

Tal como se aprecia en la imagen N°08, a pesar de lo corto que pudiese resultar la excitación externa “p(t)”, en condición de resonancia, en el tiempo de 4.04 segundos ya se ha alcanzado el 100% de “uo”. No obstante, esto no debe alarmarnos, debido a que la fracción de amortiguamiento crítico “ξ” que tiene este sistema estructural, permite que el desplazamiento dinámico máximo “uo” sea de:

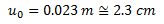
Es decir, no es un desplazamiento dinámico tan grande como el caso de estudio N°02. Una vez realizado el estudio de la influencia de la fracción de amortiguamiento crítico “ξ” y de la duración de la excitación externa “p(t)”, para la condición de resonancia en las respuestas dinámicas máximas a desarrollar por el sistema estructural, procederemos a extrapolar estos conceptos al campo de la ingeniería sismoresistente, realizando un análisis cualitativo de los efectos de los sismos de larga duración.

INTERPRETACIÓN CUALITATIVA DE LOS EFECTOS DE LOS SISMOS DE LARGA DURACIÓN EN LAS ESTRUCTURAS

Teniendo claro los conceptos de la dinámica estructural desarrollados en los tópicos anteriores, podemos extrapolarlos al campo de la ingeniería sismoresistente, donde la excitación dinámica externa está representada por un sismo. A diferencia de una fuerza armónica que se supone aplicada en la masa (ver imagen N°05), la carga sísmica, se transmite a través del terreno de fundación, actuando por consiguiente en la base de la estructura. Este hecho se ilustra en la siguiente imagen:

Imagen N°09: excitación en la base de la estructura por acción de un sismo

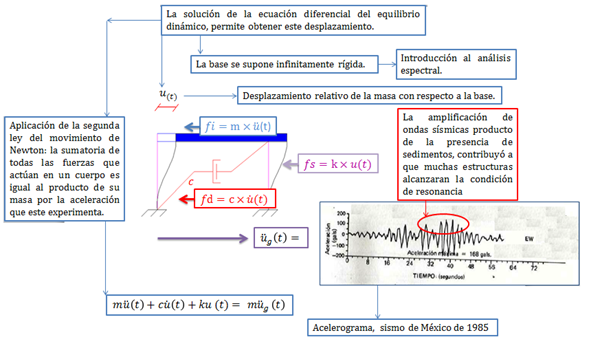
Fuente: Sauter (1989) adaptada por Santana (2018)

Vale destacar que la excitación del terreno provocada por un sismo, produce un desplazamiento del terreno propiamente dicho y un desplazamiento relativo de la masa con respecto a la base “u(t)” (ver imagen N°09), centrando la atención en este último, que produce condiciones de esfuerzos y deformaciones, similar a la aplicación de la carga en la masa como ocurría en los casos anteriormente abordados. Este principio de deformación se utiliza en el método de análisis espectral sobre el cual estaré profundizando en futuras publicaciones.

Ahora bien, el desplazamiento dinámico relativo de la masa con respecto a su base “u(t)” provoca el surgimiento de fuerzas inerciales “fi”, de amortiguamiento “fd” y de restitución elástica “fs”, que tienden a devolver el sistema a su posición original. Basados en la segunda ley de Movimiento de Newton, se obtiene la ecuación de equilibrio dinámico del sistema. La resolución de esta ecuación diferencial, requiere del uso de métodos numérico, y de métodos simplificados donde destaca el método de análisis espectral. Conviene señalar, que en los casos donde el sistema incursiona más allá del rango de comportamiento elástico, la fuerza de restitución "fs" es expresada como una función del sentido de la deformación "u". En la referencia N°06, se hace un abordaje de estas ideas.

Vale destacar que la excitación sísmica tomada como referencia, corresponde al sismo de México del 19 de septiembre del año de 1985, con una magnitud de 8.1. A diferencia de la magnitud de un sismo, que es un valor único (ver referencia N°08), intrínsecamente vinculado con el tamaño del terremoto, la aceleración, es una medida cuantitativa de la intensidad de un sismo, y varía de acuerdo a las condiciones locales, donde destaca por ejemplo, la presencia de sedimentos.

Para el sismo en cuestión, con una duración por encima de los 60 segundos, en la medida que las ondas se alejaban de la fuente de origen, su amplitud incrementaba, producto de la condición de presencia de sedimentos, lo que evitó que las ondas sísmicas se atenuaran con facilidad, presentando así la tendencia de tomar un periodo constante (función cuasi-armónica), lo cual aunado a la larga duración del evento, las estructuras cuyo período natural “Tn” coincidió con el período de la excitación externa “T”, entraron en resonancia y su colapso fue inminente.

Muchas son las enseñanzas prácticas que dejó este evento, una de ellas, es relativa a los problemas de atenuación de las ondas sísmicas, cuando existe la presencia de sedimentos. Otro aspecto, es que la condición de resonancia en las estructuras, normalmente las lleva más allá de un rango de comportamiento elástico; sugiriendo el desarrollo de amortiguamiento a través de daño. El reto del diseño sismoresistente, es garantizar un daño contralado que evite el colapso de la estructura; adicionalmente la presencia de sedimentos, ha de hacer un llamado de atención a nosotros como estudiosos de la ingeniería sismoresistente, y tomar medidas en aquellos aspectos que podemos controlar, representados por el período natural “Tn” y frecuencia natural “ωn”" de la estructura que se desea proyectar.

Es decir, si le conferimos mayor rigidez “K” a la estructura, estaríamos reduciendo su periodo “Tn”, y con ello, la estaríamos alejando de los períodos “T” de estos sismos de larga duración, y por ende de la condición de resonancia. Otro aspecto de importancia, y que se demostró en los tópicos anteriores, es la influencia del amortiguamiento; mientras este era mayor, pese a la condición de resonancia, la deformación dinámica máxima “uo” disminuía, con la consecuente disminución del número de ciclos “j”. Este hecho abre también las puertas a pensar en dispositivos especiales de amortiguamiento, en zonas de elevada amenaza sísmica.

CONCLUSIONES

El estudio de la dinámica estructural, a través de casos ideales, y excitaciones externas de función bien definida, por ejemplo, una función armónica, sin lugar a dudas que nos da una base para adentrarnos en tópicos especializados de la ingeniería sismoresistente, dado que se afianzan principios de importancia de enorme interés práctico, los cuales a modo de conclusión se resumen a continuación:

1.- La fracción de amortiguamiento crítico “ξ” incide en la cantidad de ciclos a desarrollar para que el sistema estructural en condición de resonancia alcance la deformación dinámica máxima “uo”.

2.- El tiempo de duración de la excitación externa “p(t)”, influye en el proceso de que la estructura alcance su máxima deformación dinámica “uo”. Se demostró que esto incide notablemente en sistemas con una fracción de amortiguamiento crítico “ξ” muy baja, en el orden de “0.01”, mucho menor, a la típicamente utilizada de “0.05”.

3.- Las estimaciones realizadas en el modelo teórico, en cuanto a las amplificaciones dinámicas esperadas, proveniente de la solución analítica de la ecuación diferencial de equilibrio dinámico, tienen una correspondencia aceptable, con las obtenidas con el uso de la herramienta computacional NONLIN V 7.14.

4.- En importante que en la formación como ingenieros sismoresistentes, profundicemos en los principios de la dinámica estructural, y los comprendamos muy bien, dado que esto nos servirá de mucha ayuda para aplicaciones avanzadas en la ingeniería sismoresistente.

FUENTES CONSULTADAS

1.- CHOPRA ANIL K. 2014. DINÁMICA DE ESTRUCTURAS. CUARTA EDICIÓN. PEARSON EDUCACIÓN, MÉXICO.

2.- SAUTER F. 1989. FUNDAMENTOS DE LA INGENIERÍA SÍSMICA I: INTRODUCCIÓN A LA SISMOLOGÍA. EDITORIAL TECNOLÓGICA DE COSTA RICA.

3.- NONLIN “EDUCATIONAL PROGRAM FOR LEARNING THE CONCEPTS OF STRUCTURAL DYNAMICS AND EARTHQUAKE ENGINEERING”. DEVELOPED BY DR. FINLEY CHARNEY, NONLIN IS AVAILABLE AS ONLINE TOOL THROUGH NEESHUB: HTTP://NEES.ORG/

4.- SANTANA E. 2018. ESTUDIO DE LA INFLUENCIA DEL AMORTIGUAMIENTO EN LA RESPUESTA DINÁMICA MÁXIMA DE UN SISTEMA ESTRUCTURAL DE UN GRADO DE LIBERTAD SOMETIDO A UNA VIBRACIÓN FORZADA ARMÓNICA. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/estudio-de-la-influencia-del-amortiguamiento-en-la-respuesta-dinamica-maxima-de-un-sistema-estructural-de-un-grado-de-libertad

5.- SANTANA E. 2018. DETERMINACIÓN EXPERIMENTAL DEL AMORTIGUAMIENTO EN ESTRUCTURAS. UN ENFOQUE MATEMÁTICO CON APLICACIONES EN LA INGENIERÍA SISMORESISTENTE. DISPONIBLE EN:https://steemit.com/stem-espanol/@eliaschess333/determinacion-experimental-del-amortiguamiento-en-estructuras-un-enfoque-matematico-con-aplicaciones-en-la-ingenieria

6.- SANTANA E. 2018. ESTUDIO DEL AMORTIGUAMIENTO MÁS ALLÁ DEL COMPORTAMIENTO ELÁSTICO DE UN SISTEMA ESTRUCTURAL CON EL USO DE CICLOS DE HISTÉRESIS. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/estudio-del-amortiguamiento-mas-alla-del-comportamiento-elastico-de-un-sistema-estructural-con-el-uso-de-ciclos-de-histeresis

7.- SANTANA E. 2018. ABORDAJE DIDÁCTICO DEL CONCEPTO DE RESONANCIA A TRAVÉS DE UN ENFOQUE MATEMÁTICO Y SUS APLICACIONES EN LA DINÁMICA DE ESTRUCTURAS. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/abordaje-didactico-del-concepto-de-resonancia-a-traves-de-un-enfoque-matematico-y-sus-aplicaciones-en-la-dinamica-de-estructuras

8.- SANTANA E. 2018. ESTUDIO DE LA MAGNITUD DE UN SISMO. UNA VISIÓN PRÁCTICA DE LOS APORTES DE LA SISMOLOGÍA. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/estudio-de-la-magnitud-de-un-sismo-una-vision-practica-de-los-aportes-de-la-sismologia