ABORDAJE DIDÁCTICO DEL CONCEPTO DE RESONANCIA A TRAVÉS DE UN ENFOQUE MATEMÁTICO Y SUS APLICACIONES EN LA DINÁMICA DE ESTRUCTURAS

INTRODUCCIÓN

En esta oportunidad vamos a estudiar un tema de mucha importancia en la dinámica estructural representado por el fenómeno de resonancia, realizando en primera instancia un abordaje matemático que permite resolver la ecuación diferencial que representa el equilibrio dinámico del sistema estructural sometido a una excitación armónica de la forma “p(t) = po sen (ωt)”; y posterior a ello, desarrollar el planteamiento necesario, que permite explicar matemáticamente el fenómeno en cuestión, que se produce cuando la frecuencia de la excitación externa (ω) se iguala con la frecuencia natural (ωn). Una vez aclarado los aspectos matemáticos del problema en estudio, utilizaremos la herramienta computacional NONLIN V 7.14 (ver ref. 2), para demostrar con ejemplos prácticos, la certeza del cálculo diferencial que nos aporta las matemáticas.

DELIMITACIÓN DE LA TEMÁTICA A ESTUDIAR

En la imagen N°01, se ilustra didácticamente los aspectos que delimitan la temática a estudiar. Destacando que la interpretación del concepto de resonancia estará basado en la respuesta estructural, en términos de fuerza cortante (V) y desplazamiento (D), de un sistema estructural con propiedades elásticas e inerciales, y con la condición de propiedades de amortiguamiento nulas, con el fin de magnificar las consecuencias del fenómeno de resonancia, producida al mismo tiempo por una vibración forzada armónica, representada por una fuerza “p(t) = po sen (ωt)” que al aplicarse en la dirección del grado de libertad de la estructura que se analiza, hace que esta vibre de en forma permanente.

Imagen N°01: ilustración didáctica del tema en estudio

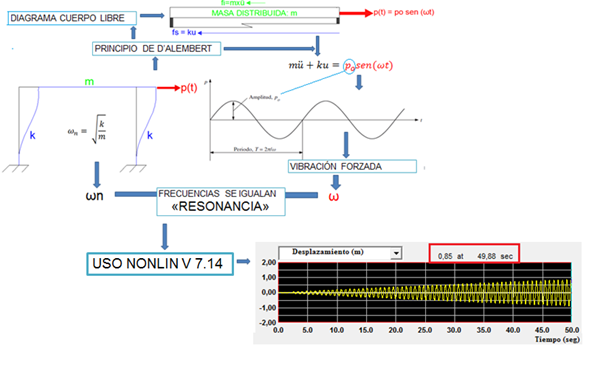
Fuente: NONLIN V 7.14, Chopra (2014) adaptado por Santana (2018)

Las propiedades elásticas (asociadas a la rigidez K) e inerciales (asociadas a la masa “m”) se pueden representar a través del principio de D’Alembert, en términos de fuerzas de restitución elástica (fs) y fuerzas inerciales (fi), las cuales se opondrán a la fuerza externa aplicada p(t), permitiendo generar la ecuación de equilibrio dinámico del sistema:

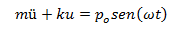
Estaremos analizando tres casos de estudio, representativos de tres posibilidades de interacción entre la frecuencia de la fuerza externa (ω) y de la frecuencia natural (ωn), haciendo especial énfasis, al hecho de cuando estas frecuencias se igualan, lo que da la bienvenida al fenómeno de resonancia.

RESOLVIENDO LA ECUACIÓN DIFERENCIAL DE FORMA ANALÍTICA

En primer lugar, vamos a resolver la ecuación de equilibrio dinámico obtenida para el sistema ilustrado en la imagen N°01, estructurando dicha solución en dos tipos: solución particular “up(t)” y solución complementaria “uc(t)”.

La solución particular se asocia directamente con la fuerza externa aplicada, de frecuencia (ω), y en términos de desplazamiento particular, se expresa:

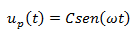
Obtengamos la primera y segunda derivada con respecto al tiempo de la solución particular, para así obtener la solución particular en términos de velocidad “ůp (t)” y aceleración “üp (t)” respectivamente:

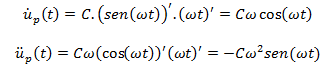
Sustituimos en la ecuación de equilibrio dinámico las soluciones particulares obtenidas:

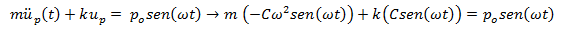
Reescribimos y sacamos factor común Csen(ωt):

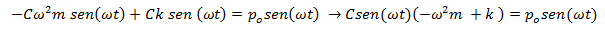
En la expresión obtenida el término “sen (ωt)” aparece multiplicando a ambos lados de la igualdad, por lo que se puede simplificar y obtener lo siguiente:

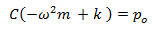
Adicionalmente la masa “m” puede ser expresada en términos de frecuencia natural (ωn), a través de la siguiente expresión:

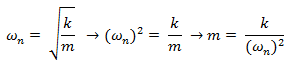
Sustituyendo:

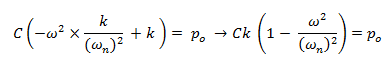
Despejamos C:

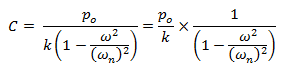
Procedemos a reescribir las soluciones particulares en términos de desplazamiento y velocidad, de la siguiente manera:

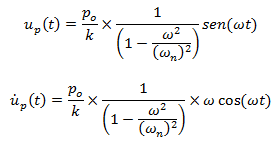
Por su parte la solución complementaria, está asociada a las propiedades dinámicas de la estructura que se analiza, por medio de su frecuencia natural (ωn); y en términos de desplazamiento y velocidad, dicha solución complementaria se expresa así:

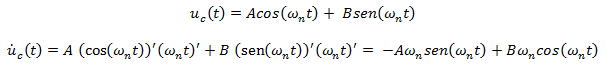
La unión de la solución complementaria y particular, sugiere el planteamiento de una solución general en términos de desplazamiento “ut” y velocidad “ůt” de la forma:

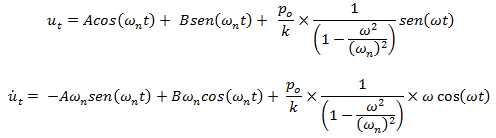
Evaluamos estas soluciones para el instante de tiempo t=0seg, y así obtener los valores de las constantes A y B:

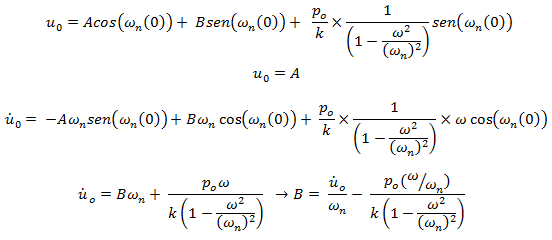
En este orden de ideas, la solución general de la ecuación diferencial de equilibrio dinámico, es:

El término resaltado en color verde, es un componente de la respuesta de desplazamiento del sistema estructural, gobernado por las propiedades naturales de este, representadas por la frecuencia natural del mismo (ωn), lo cual puede ser concebido como la respuesta en vibración libre (ver ref. 3). Por su parte el componente resaltado en color azul, es el aporte a la respuesta de desplazamiento proveniente de la fuerza externa aplicada de frecuencia (ω), la cual transmite vibración al sistema de forma permanente. Al evaluar la solución general para las condiciones abajo señaladas, se obtiene la gráfica de la imagen N°02:

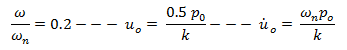
Imagen N°02: respuesta de sistema no amortiguado ante una fuerza armónica

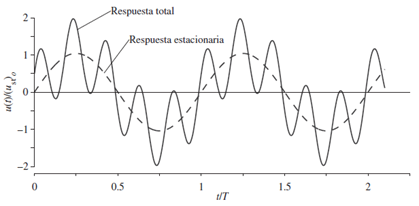
Fuente: Chopra (2014)

El aporte al desplazamiento derivado de la condición de vibración libre, no lo estaremos considerando para fines prácticos; para así enfocarnos directamente en la respuesta estacionaria producto de la vibración forzada. Este hecho permite simplificar la solución general:

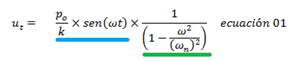
El componente resaltado en color azul, es la deformación estática (ust) del sistema despreciando los efectos inerciales productos de la excitación de la masa; lo cual puede ser comprobado a partir del siguiente abordaje a la ecuación de equilibrio dinámico del sistema, como se demuestra a continuación:

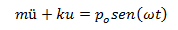
Considerando que el término mü = 0 y despejando “u=ust”, obtenemos:

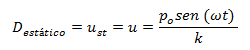
Por lo tanto la máxima deformación estática (Dmax estática = ust max) que podemos obtener es:

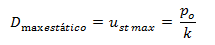
Y la fuerza cortante máxima para el caso estático es:

La obtención de las respuestas estáticas permite introducir un concepto de mucha importancia, como lo es el “factor de amplificación dinámica Rd”, el cual es un cociente que resulta de dividir la respuesta dinámica con respecto a la respuesta máxima estática:

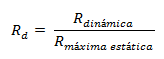
Este factor está fuertemente vinculado a la interacción de frecuencias, por lo que conceptualmente se puede representar con el término resaltado en color verde, de la ecuación 01, de la forma:

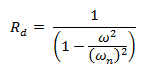
Esta expresión, permite sustentar los tres casos de análisis, que se abordarán a lo largo de este trabajo; los mismos se explican a continuación de una forma conceptual y matemática, y serán la referencia de los ejemplos prácticos a desarrollar con ayuda de la herramienta computacional NONLIN V 7.14:

Caso N°01, la fuerza armónica varía lentamente, es decir, periodos largos; lo cual matemáticamente se puede representar así:

Para el caso N°01, el periodo de la vibración forzada es mucho más grande que el periodo natural de la estructura, y atendiendo al hecho de que el periodo es el tiempo para completar el ciclo de una oscilación (ver ref. 3), esto nos sugiere que la fuerza externa aplicada varía lentamente. Para un periodo (T) extremadamente grande, la frecuencia (ω) por ser el inverso del periodo, es extremadamente pequeña, por lo que el cociente que resulta de dividirla por la frecuencia natural (ωn) tiende a 0; si este cociente se avalúa en la expresión del factor de amplificación dinámica, tenderá a ser ligeramente mayor que 1, es decir, la deformación dinámica es aproximadamente igual a la deformación estática.

Caso N°02, la fuerza armónica varía rápidamente, es decir, períodos cortos; lo cual matemáticamente se puede representar así:

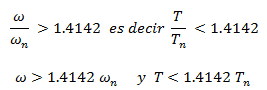
Estas relaciones se pueden interpretar, asociando un periodo muy corto (T) de la fuerza externa, con una frecuencia (ω) de excitación alta, lo que originaría en el cociente que resulta de dividir esta por la frecuencia natural (ωn) un número muy grande, ocasionando que el factor de amplificación dinámica "Rd" tienda a cero “0”, interpretándose este aspecto, en el hecho de que la fuerza varía tan rápido que no hay excitación de las masas, y el problema se convierte en un problema estático.

Caso N°03, la frecuencia natural (ωn) y la frecuencia de la fuerza externa (ω) tienden a igualarse, por lo que:

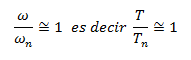
Al evaluar el cociente que resulta de dividir las frecuencias mencionadas, cuyo resultado es aproximadamente la unidad, en la expresión de factor de amplificación dinámica "Rd", hace que el mismo tienda a infinito, es decir, la respuesta dinámica es extremadamente grande en comparación con la respuesta estática; cuando estas condiciones se dan, se dice que estamos en presencia de RESONANCIA. En la imagen N°03, se ilustran los casos estudiados de forma gráfica:

Imagen N°03: representación gráfica de casos estudiados

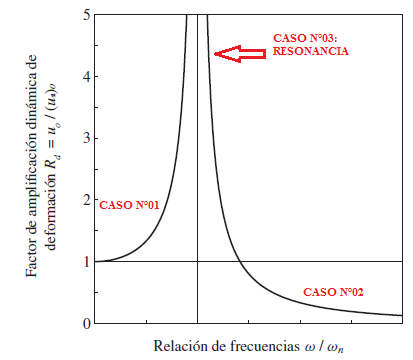
Fuente: Chopra (2014) adaptado por Santana (2018)

Como podemos apreciar en la gráfica de la imagen N°03, el caso crítico es el de resonancia, donde la amplificación dinámica tiende al infinito, por lo que es de mucho interés conocer el proceso de la evolución de la respuesta dinámica en el tiempo bajo esta condición, desde un enfoque matemático, lo cual se aborda en el siguiente tópico.

LA RESONANCIA, DESDE UN ENFOQUE MATEMÁTICO

El estudio de la resonancia requiere de una sustentación matemática, que permita demostrar que el incremento abismal del factor de amplificación dinámica con tendencia al infinito, no ocurre, de forma inmediata al igualarse la frecuencia de excitación de la carga externa (ω) y la frecuencia natural del sistema (ωn). Procederemos de este modo, a resolver la ecuación diferencial de equilibrio dinámico para esta condición de frecuencias iguales, demostrando que la solución particular de la forma:

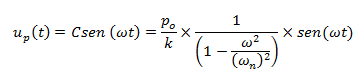
No cumple para el caso de frecuencias iguales “resonancia”, porque la solución general, evaluada en condiciones iniciales de desplazamiento (uo=0) y velocidad (ůo=0), da como resultado:

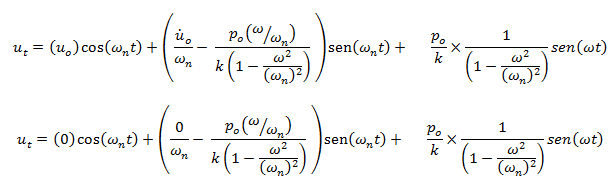
Sin reescribimos y sacamos factor común, obtenemos:

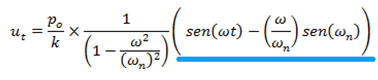
Y como en condición de resonancia, las frecuencias son iguales, el término resaltado en azul se cancela, anulándose la expresión general de desplazamiento para esta condición. Por lo tanto Chopra (2014) sugiere como solución particular:

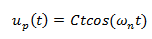
La primera derivada con respecto al tiempo de esta solución particular es:

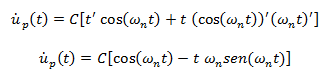
Procedemos a obtener la segunda derivada con respecto al tiempo:

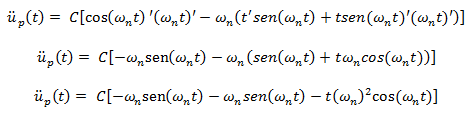
Sustituimos en la ecuación de equilibrio dinámico:

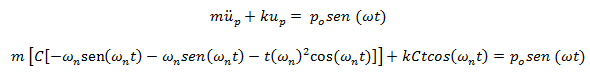
Al expresar la masa en términos de frecuencia natural de la forma:

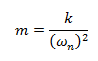
Y sustituyendo:

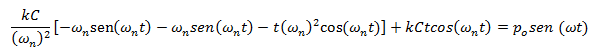
Reescribimos:

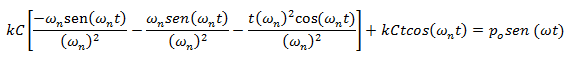
Simplificando y aplicando la propiedad distributiva:

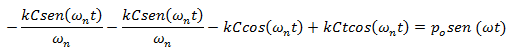
Reescribiendo se tiene lo siguiente:

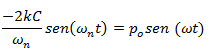
El término sen (ωnt) = sen (ωt), por el caso de frecuencias iguales que estamos trabajando, y como aparece multiplicando en ambos lados de la ecuación, se puede simplificar quedando:

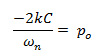
Despajamos C:

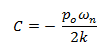
Por lo que la solución particular en términos de desplazamiento queda:

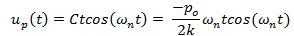
Y en términos de velocidad:

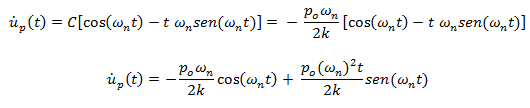
La solución general en términos de desplazamiento y velocidad, evaluada en condiciones iniciales de t=0 seg, para obtener los valores de las constantes de integración A y B, asociadas a la respuesta complementaria de vibración libre es:

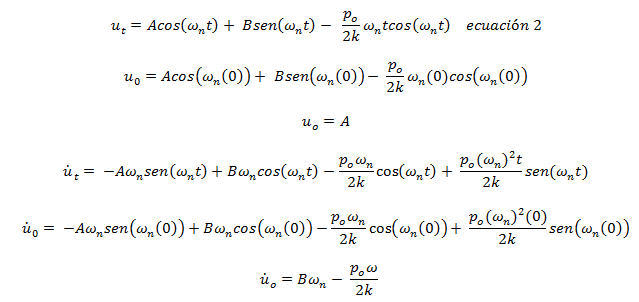
Despejando B:

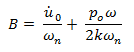
Partiendo del hecho de que las frecuencias son iguales por el caso de estudio:

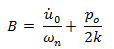
Si establecemos las condiciones iniciales de desplazamiento “uo = 0” velocidad “ůo = 0”, las constantes de integración son:

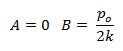
Estos valores de “A” y “B” los sustituimos en la ecuación 02:

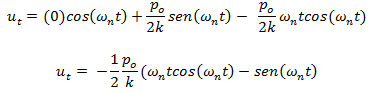
Partiendo del hecho de que:

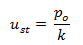
Entonces la solución general de la ecuación de equilibrio dinámico en condición de resonancia, viene dada por:

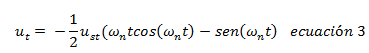
Esta solución general puede ser reescrita, introduciendo el concepto de amplificación dinámica:

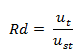
Por lo que dividimos la ecuación 03 por ust:

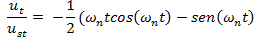
Y si expresamos la frecuencia natural, en términos de periodo natural de la forma:

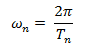
La expresión para el factor de amplificación dinámica es:

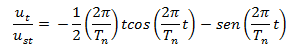
En imagen N°04 podemos observar la representación gráfica de esta función:

Imagen N°04: respuesta de un sistema no amortiguado en condición de resonancia

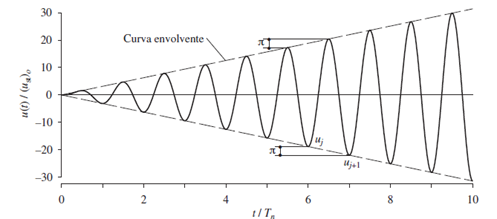
Fuente: Chopra (2014)

Al analizar la gráfica, nos damos cuenta que la tasa de crecimiento de la amplitud está dada por:

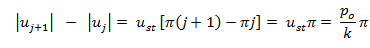
Y en la medida que la duración de la vibración se incremente, la amplificación dinámica lo hará en consecuencia, con tendencia al infinito. A continuación realizaremos aplicaciones numéricas con ayuda de la herramienta computacional NONLIN V 7.14, para aplicar los casos estudiados a una estructura real como la que se puede apreciar en la imagen N°05.

PROPIEDADES ELÁSTICAS, INERCIALES Y DINÁMICAS DE LA ESTRUCTURA EN ESTUDIO

Tomemos como referencia un pórtico plano de un nivel, con un grado de libertad tanto estático como dinámico como el ilustrado en la imagen N°05:

Imagen N°05: estructura en estudio

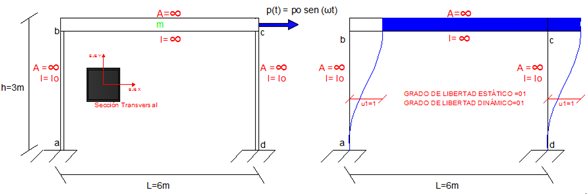
Fuente: Santana (2018)

Las propiedades elásticas (rigidez “K”), inerciales (masa “m”, peso “W”) y dinámicas (período natural “Tn” y frecuencia natural “ωn” o “fn”) de la estructura en estudio, se especifican en la tabla N°01:

Tabla N°01: propiedades elásticas inerciales y dinámicas de la estructura en estudio

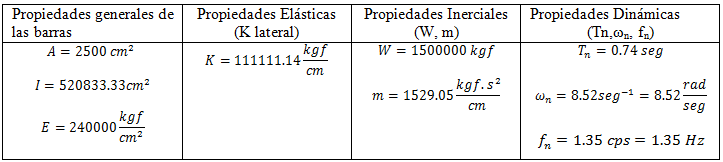
Fuente: Santana (2018)

Para una mejor comprensión de las propiedades plasmadas en la tabla N°01, el autor recomienda revisar la referencia N°03; a los fines de afianzar el proceso de obtención de cada una de ellas.

ESTIMACIÓN DE PROPIEDADES DINÁMICAS EN EL PROGRAMA NONLIN VERSIÓN 7.14

Vale destacar que las propiedades dinámicas dependen de las propiedades elásticas e inerciales; las cuales se introducen en el programa NONLIN V 7.14, realizando previamente una conversión de unidades, como se demuestra a continuación:

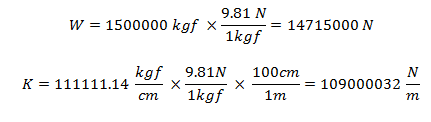
Imagen N°06: vista de propiedades elásticas, inerciales y dinámicas en el NONLIN V 7.14

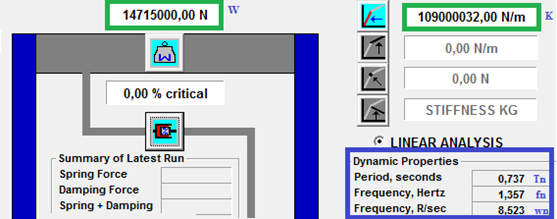
Fuente: NONLIN V7.14, adaptado por Santana (2018)

Podemos apreciar en la imagen N°06, las propiedades dinámicas resaltadas con el recuadro azul, las cuales al compararse con las de la tabla N°01, son aproximadamente iguales, siendo la mínima diferencia por errores de redondeo del cálculo manual; sin embargo, esto da a entender que las propiedades elásticas e inerciales fueron introducidas correctamente en el programa. Procedamos ahora, a analizar la respuesta estructural en términos de desplazamiento lateral (D) y fuerza cortante (V) ante una vibración forzada armónica, para distintos valores de frecuencia (ω) que engloben los tres casos de estudio plasmados en la imagen N°03, trabajando en el programa NONLIN V 7.14 con el inverso de la frecuencia, es decir, el Periodo (T).

OBTENCIÓN DE LA RESPUESTA ESTRUCTURAL EN TÉRMINOS DE DESPLAZAMIENTO Y FUERZA CORTANTE

Al someter el sistema estructural a una excitación armónica este responderá en función a las características de dicha excitación; la cual está regida por la siguiente función:

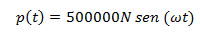
Dónde:
N= Newton
Po = 500000 N

Conviene aclarar que los valores de frecuencia de la excitación externa, variaran conforme a los casos de estudio, y en el programa NONLIN V 7.14, se trabajará con su inverso, es decir, el Periodo (T). La respuesta de la estructura que estaremos evaluando serán la fuerza cortante (V) que experimenta y el desplazamiento (D), como se ilustra en la imagen N°07.

Imagen N°07: ilustración de la respuesta a obtener en términos de desplazamiento y fuerza cortante

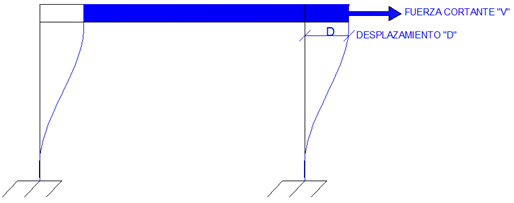
Fuente: Santana (2018)

Adicionalmente, vale calcular la respuesta de la estructura desde un enfoque estático, es decir, despreciando los efectos inerciales de excitación de las masas; lo cual será un punto de comparación para estimar cuantitativamente el nivel de amplificación dinámica obtenido para cada caso de estudio. En este orden de ideas, se tiene que:

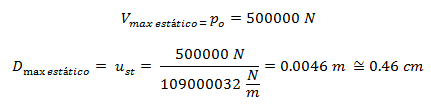
CASO N°01. La fuerza varía lentamente, es decir su periodo es largo, en comparación con el periodo natural, por lo que:

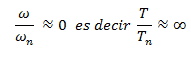
Para lograr esta condición en el programa NONLIN V 7.14, se toma como referencia el periodo natural Tn = 0.74 seg, asignando un valor de periodo (T) de la excitación externa mucho mayor, como se ilustra a continuación:

Imagen N°08: características de la vibración forzada, para el caso N°01

Fuente: NONLIN V7.14, adaptado por Santana (2018)

La respuesta de la estructura en el tiempo de duración de la excitación armónica se ilustra a continuación:

Imagen N°09: respuesta de la estructura en términos de desplazamiento y fuerza cortante, caso N°01

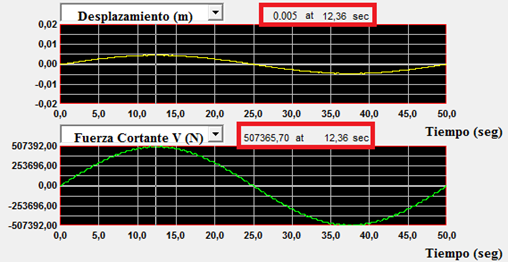
Fuente: NONLIN V7.14, adaptada por Santana (2018)

Aproximadamente en el tiempo de 12.36 seg , las respuestas obtenidas son:

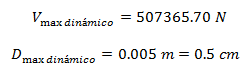
Estos valores, al contrastarlos con la respuesta estática, permite obtener los siguientes cocientes indicativos de la amplificación dinámica (Rd) alcanzada:

Se demuestra que el factor de amplificación dinámica, es muy cercano al valor de la unidad, es decir, la respuesta dinámica máxima es aproximadamente igual a la respuesta estática máxima.

CASO N°02. La fuerza armónica varía rápidamente, períodos cortos; la forma matemática de expresarlo es la siguiente:

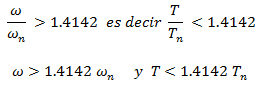
Para lograr esta condición en el programa NONLIN V 7.14, se toma como referencia el periodo natural Tn = 0.74 seg :

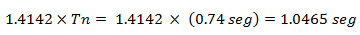
Lo que significa que el período de la excitación armónica debe ser menor a 1.0465 seg, dicha condición se logra en el programa NONLIN V 7.14 de la siguiente manera:

Imagen N°10: características de la vibración forzada, para el caso N°02

Fuente: NONLIN V 7.14 adaptada por Santana (2018)

La respuesta de la estructura en el tiempo de duración de la excitación armónica se ilustra a continuación:

Imagen N°11: respuesta de la estructura en términos de desplazamiento y fuerza cortante, caso N°02

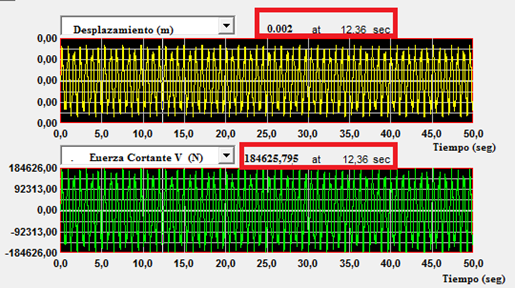
Fuente: NONLIN V 7.14, adaptado por Santana (2018)

Aproximadamente en el tiempo de 12.36 seg , las respuestas obtenidas son:

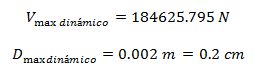
Estos valores, al contrastarlos con la respuesta estática, permite obtener los siguientes cocientes indicativos de la amplificación dinámica (Rd) alcanzada:

Lo que demuestra que cuando la fuerza externa aplicada varía muy rápido (periodos cortos), en comparación con el período natural de la estructura, la respuesta dinámica es mucho menor que la respuesta estática.

CASO N°03. La frecuencias natural (ωn) y la frecuencia de la fuerza externa (ω) tienden a igualarse, por lo que:

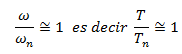
Para lograr esta condición en el programa NONLIN V 7.14, se toma como referencia el periodo natural Tn = 0.74 seg, asignando ese mismo valor al periodo (T) para la excitación externa, como se aprecia en la siguiente imagen:

Imagen N°12: características de la vibración forzada, para el caso N°03

Fuente: NONLIN V 7.14, adaptado por Santana (2018)

La respuesta de la estructura en el tiempo de duración de la excitación armónica se ilustra a continuación:

Imagen N°13: respuesta de la estructura en términos de desplazamiento y fuerza cortante, caso N°03

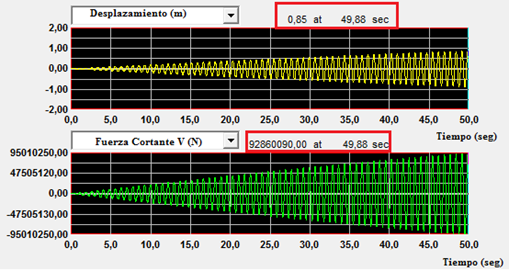
Fuente: NONLIN V 7.14, adaptado por Santana (2018)

Nos damos cuenta como en la medida que transcurre el tiempo, las respuestas en términos de desplazamiento y fuerzas cortantes tienden al infinito. Aproximadamente en el tiempo de 50 seg , las respuestas obtenidas son:

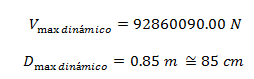
Estos valores, al contrastarlos con la respuesta estática, permiten obtener los siguientes cocientes indicativos de la amplificación dinámica producida en condición de resonancia:

Es decir, que la respuesta dinámica excede por lo menos ciento ochenta veces a la respuesta estática; y como estamos en un caso de vibración forzada sin amortiguamiento, si esta, tuviese más duración, la amplificación dinámica seguiría aumentando con tendencia al infinito.

CONCLUSIONES

1.- La condición de resonancia es producida cuando la frecuencia de la fuerza externa aplicada coincide con la frecuencia natural del sistema estructural.

2.- El factor de amplificación dinámica es una medida cuantitativa de las respuestas dinámicas máximas que experimenta el sistema estructural con respecto a la respuesta máxima estática; por lo que el problema dinámico cobra importancia, cuando el factor de amplificación dinámica es superior a la unidad.

3.- Las propiedades dinámicas de una estructura, dependen de las propiedades elásticas (rigidez) y de las propiedades inerciales (masa), por lo que si se quiere librar a una estructura de la condición de resonancia, se puede hacer, disminuyendo su periodo natural y por consiguiente aumentando su frecuencia natural; haciéndola mayor a la de la excitación externa.

4.-Los estudios desarrollados, son una introducción a temas avanzados de la dinámica estructural, especialmente cuando es una función sísmica lo que representa la fuerza externa aplicada; por eso la importancia de dominar estos aspectos, en la formación como ingenieros sismoresistentes.

REFERENCIAS CONSULTADAS

1.- CHOPRA ANIL K.DINÁMICA DE ESTRUCTURAS. CUARTA EDICIÓN. PEARSON EDUCACION, MEXICO 2014.

2.-.NONLIN “EDUCATIONAL PROGRAM FOR LEARNING THE CONCEPTS OF STRUCTURAL DYNAMICS AND EARTHQUAKE ENGINEERING”. DEVELOPED BY DR. FINLEY CHARNEY, NONLIN is available as online tool through NEEShub: http://nees.org/

3.- SANTANA ELÍAS. COMPRENDIENDO LAS APLICACIONES DE LAS MATEMÁTICAS EN LA ESTIMACIÓN DEL PERIODO Y FRECUENCIA NATURAL DE UN PORTICO PLANO. CASO: SISTEMA DE UN GRADO DE LIBERTAD. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/comprendiendo-las-aplicaciones-de-las-matematicas-en-la-estimacion-del-periodo-y-frecuencia-natural-de-un-portico-plano-caso