"Singapore Math" : The Cows and Goats Problem

The following mathematics word problem is not from Waikikamukau (why kick a moo cow?), but from some school in Singapore, at probably around the equivalent of grade 5. It is meant to goad (goat?) pupils into learning more deeply about percentages and fractions. These word problems are often hard, even for adult parents trying to help their own children, or other people's children.

Stop! Think about the problem for a while.
Try solving it yourself first.
.
.
.
Resist
.
.
.
the
.
.
.
temptation
.
.
.
to
.
.
.
peep
.
.
.
at
.
.
.
my
.
.
.
elegant
.
.
.
simple
.
.
.
solution
.
.
.
below,
.
.
.
lest
.
.
.
you
.
.
.
think
.
.
.
it
.
.
.
is
.
.
.
sooooooooooooooooooooo
.
.
.
very
.
.
.
easy.
.
.
.
My solution looks easy only because I had thought hard about this sort of problem over many years, and sought a way to simplify the process as well as the presentation to make it very succinct, so that it is easy to learn, and everybody (young and old) can cut to the chase.
People tend to have a bias. They think a longer solution is better. Just like stupid bosses / accountants / human resource managers think programmers did more work if their code is longer. It is actually harder to think and come up with a short solution. A longer solution to a maths problem tends to take longer, and increases the chances of making careless mistakes. Similarly, longer "spaghetti" computer code shows lack of organisation, lack of efficiency and increases errors.
Mathematics is about striving for elegence and simplicity, not just blindly following procedures. It is so much an art, as well as a science. If a pupil learns mathematics well, he or she can do anything, be it art, science or computer programming.
.
.
.
So
.
.
.
I
.
.
.
would
.
.
.
encourage
.
.
.
you
.
.
.
to
.
.
.
have
.
.
.
a
.
.
.
go
.
.
.
at
.
.
.
the
.
.
.
problem
.
.
.
for
.
.
.
a
.
.
.
little
.
.
.
while
.
.
.
longer.
.
.
.
Don't peep!
.
.
.
Don't give up yet!
.
.
.
You may try using algebra. However it is not necessary.
.
.
.
Now, have you tried hard enough already?
Did you manage to solve it?
Does your solution make sense?
OK, you may compare with my solution below.
Solution
First I read the word problem sentence by sentence, and translate the information into my Distinguished Ratio Units (DRU) diagram.
"3/4 of the cows are sold" means 1/4 of the cows remain. That means the ratio of number of cows in the "after" situation compared to that "before", is 1 : 4. "60% of the goats are sold" means 40% i.e. 2/5 remain. So the "after : before" ratio is 2 : 5 for the goats. I use different shapes to envelope the different ratio units, say circles for the cows and squares for the goats. By the way, using "before" vs "after" analysis is one of the heuristics recommended by the Singapore Ministry of Education.
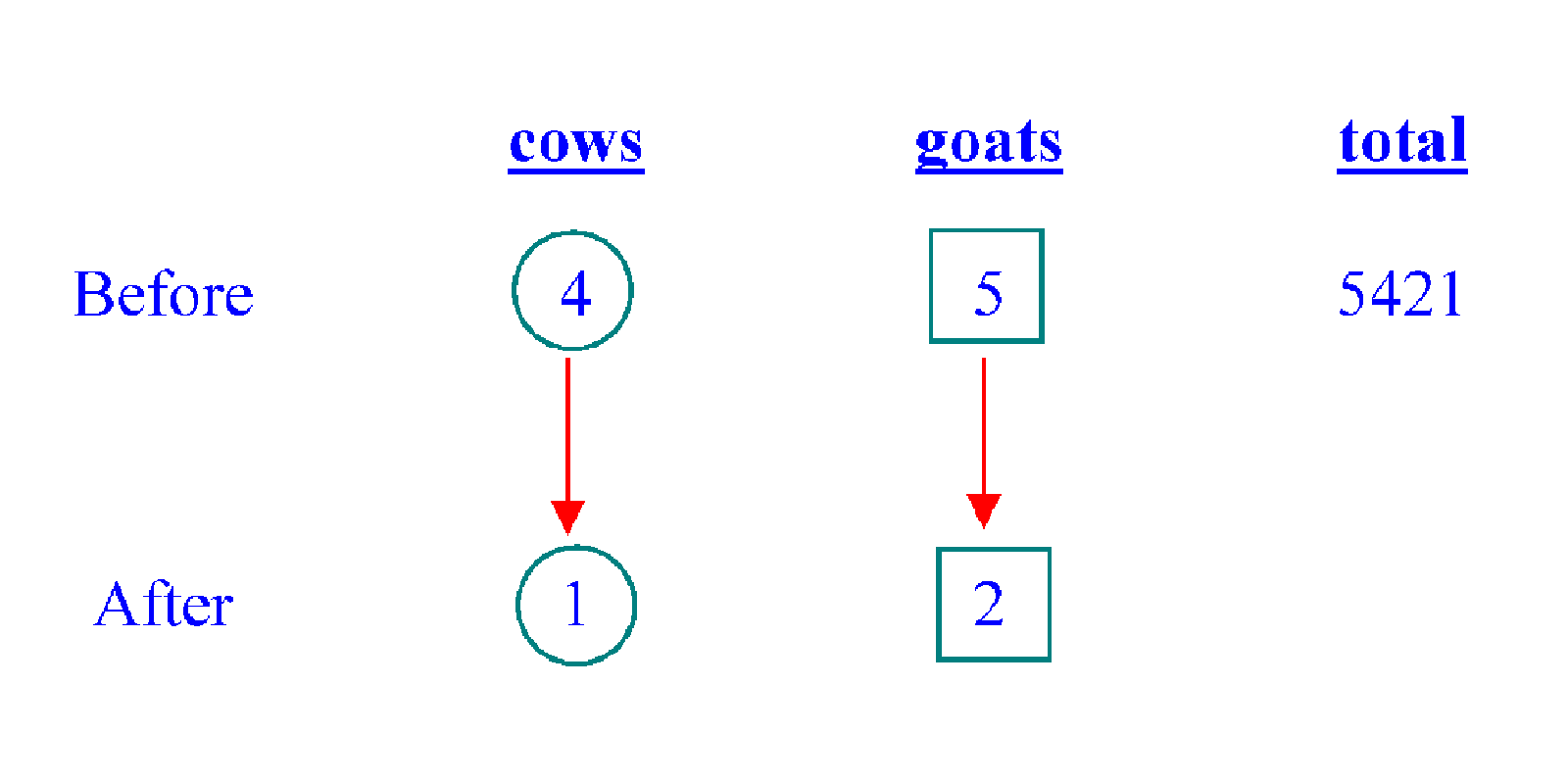
Ratio units are not the same as absolute numbers. So, for example, the circled 4 units does not mean there are 4 cows. The actual number of cows is some multiple of 4 i.e. 4 times something, but we do not know what it is yet. Furthermore, the units for the cows are different from the units for the goats. Thus, a "4 units" for the cows would not mean the same thing as "4 parts/units" for the goats. That is why I mark the units differently, so as not to confuse between them. Some people would write, say, "4u" for the cows and "5p" for the goats. That works too.
We know that the 4 "circle" units for the cows plus the 5 "square" units for the goats add up to the total of 5421. Our problem is: the units are different. So we cannot meaningfully do the addition yet. However, there is one more clue that we still have not used. It is the fact that in the "after" situation, there will be the number of cows will be the same as the number of goats. This is a crucial piece of information. From here we know that each "circle" unit is the same as 2 "square" units. So we can change the "circle" units, via multiplication by 2 in the "cows" column, to square units.
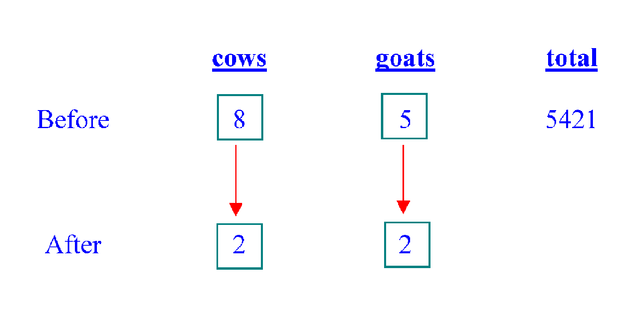
After equalising the units in the "after" situation (based on the clue given), we now figure out that we have the equivalent of 8 "square" units for the cows in the "before" situation. Now we can add up the "square" units in the "before" situation.
8 + 5 = 13 "square" units is the same as 5421. Dividing by 13, we deduce that 1 "square" unit is 417. Multiplying 417 by 8 and by 5, we get the respective numbers for the cows and the goats. We have 8 × 417 = 3336 and 5 × 417 = 2085. Hence our final answer is as follows:-
There are 3336 cows and 2085 goats.
Post-mortem Reflections
You may have heard that "Singapore Math" uses the Bar Diagramming Method (a.k.a. the "model" method). Well, bar models are a good way for visualising and learning. Nevertheless, it is not the only way, nor the best way sometimes. Bar modelling is only one of the many ways of drawing diagrams, which is only one of the 11 recommended heuristics for primary school (elementary school) mathematics.
We should be flexible and explore other methods of solution. Actually, for maths, any systematic and clear way of presenting the information from the problem often leads easily to the solution. So the first step in solving any mathematical problem is to understand what is given and what is required, and organise the given information in same form (e.g. table, or some diagram).
I hope you have learned something in this article that empowers you to "cut the Gordian knot".
Image Credits
The first picture was derived from Pixabay, while the rest are all my own work. @originalworks
Announcements
You might also want to read my recent articles:
Inequality: Always, sometimes or never?
Integral of 1/sqrt(e^2x+1) (Trigo Approach)
Simplifying Roots
If you find my articles useful or interesting, please upvote and resteem them! Thanks !
Cheers!!!
@tradersharpe
-- promoting sharp minds
I'm not fond of drinking alcoholic beverage but between Math and Beer? I'd rather choose to be drunk.🍺🍻
40% is 160% of 25%
5421= 260% of the number of goats. That's how I got it. really fun post. Do more of these. I'm following you.
Did it the same way :)
img credz: pixabay.com
Nice, you got a 8.0% @minnowbooster upgoat, thanks to @tradersharpe
Want a boost? Minnowbooster's got your back!
This post has received a 1.92 % upvote from @booster thanks to: @tradersharpe.