Problem Solving - Running in Circles?
Do you find that you are "running in circles" when you are trying to solve mathematical problems? Take a look at the problem below, which incidentally, is about "running in circles", which I got from a Facebook friend.
Although mathematical problems are sometimes intractable even to the smartest geniuses, there is a general systematic approach to solving mathematical problems as follows:-
Step 1. Understanding the problem
Step 2. Devising a plan
Step 3. Carrying out the plan
Step 4. Checking your work
Step 5. Looking back (Review / Reflection)
The steps are based on George Pólya's 1945 book How to Solve It, although in his book, steps 4 and 5 are part of the same step. Singapore's Ministry of Education adopts a similar framework for mathematical problem-solving. Let us apply this framework to tackling the "running in circles" problem posed above.
Step 1. Understanding the problem
Ask yourself the following questions:-
- What is the given in the problem?
- What is the unknown in the problem?
- What concept is the problem testing you on?
- Did you remember to include all the relevant information?
- How are you going to organise the given information?
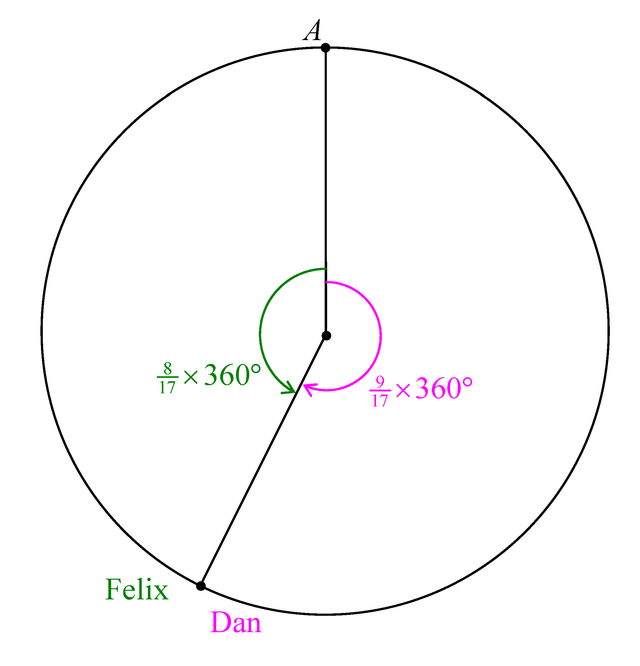
Felix and Dan run around a circular track.
They start at the same point A.
They end when both meet again at point A.
Felix is moving at 8 m/s (metres per second).
Dan is moving at 9 m/s in the opposite direction.
We are asked how many times they meet (excluding the first and the last time at point A).
Step 2. Devising a plan
Ask yourself the following questions:-
- Have you seen a similar problem before?
- How was it solved the last time?
- How is it different this time?
- What strategy or method do you intend to use?
I vaguely remember seeing this problem before, but I forgot how I solved it. So it is almost as if this is new to me. At first I thought that the answer depended on the size (radius or circumference) of the track. Later I realised that this is not necessary. If the circle was very large, the two might never meet again, but we are talking about a more realistic situation here.
The strategy can involve the use of a heuristic. One good heuristic is to draw a diagram.
Draw an imaginary line segment from the centre of the circle to the point A. Draw another imaginary line segment from the centre to the meeting point. These form an angle. Since Felix and Dan run at a speed ratio of 9 : 8, the distance on the track, and hence the angle also has this same ratio. From this diagram, I get a valuable insight. The answer would be the same whether the radius is large or small, so the radius is irrelevant. It is the angle covered that matters. For Felix, this angle is , or 8/17 of a full turn. The total number of ratio parts is 9+8 = 17, and Felix's share is 8 parts out of that 17. Every time they meet, Felix would cover another 8/17 of a full turn. Based on this observation, we may use algebra (for example) to solve the problem.
Step 3. Carrying out the plan
Ask yourself the following questions:-
- Can you explain what you are doing?
- Are you doing it the right way?
- Is there a safer method?
- Is there a faster method?
Here is my final solution.
At first, I used degrees and had a mistake in my equation. I realised it is much easier if I just counted the number of full-turns. So I went back to edit my solution.
Step 4. Looking back
Ask yourself the following questions:-
- Have you answered the problem?
- Did you miss out anything?
- Does your solution feel right?
- How do you know your solution is correct?
- Have you checked your solution?
It is important to check through the work, and check that it makes sense. If you have tried some strategy and are stuck somewhere, do not keep on doing the same thing. You may want to go back to step 2 and adopt a new strategy.
Step 5. Review / Reflection
Ask yourself the following questions:-
- How could you have done better?
- Have you discovered any tips that you can use in future?
- Can you link this problem to some other subject or
real-life problem? - Can you make up a similar problem?
- Is there another way to solve the problem?
Here are my reflections for solving this problem.
- I should avoid making unnecessary assumptions e.g. that
the answer depends on the radius. - I should try to keep my working as simple as possible e.g.
using the number of full round turns as my unit, instead of using degrees (it is not wrong,but a bit messier).
Once again, here is the 5 steps to solving mathematical problems, in a nutshell:-
- Understanding
- Strategising
- Execution
- Evaluation
- Reflection
That spells USEER ... Hope this is user-friendly enough for you to remember.
Reference
Pólya, George (1945). How to Solve It. Princeton University Press. ISBN 0-691-08097-6.
Image Credit
The first image was modified from Pixabay, while the rest are all my own work.
Announcements
I have just started a MeetUp Group, based in Singapore.
Singapore High-Achiever Parents Support Group
You might also want to read my recent articles:
A Short and Sweet Proof via Factor Theorem
Two Squares in a Circle Problem
If you find my articles useful or interesting, please upvote and resteem them! Thanks !
Cheers!!!
@tradersharpe
-- promoting sharp minds



yes
@tradersharpe thank you appeal to @sportic. Your post and will see more than 3.5K of my followers