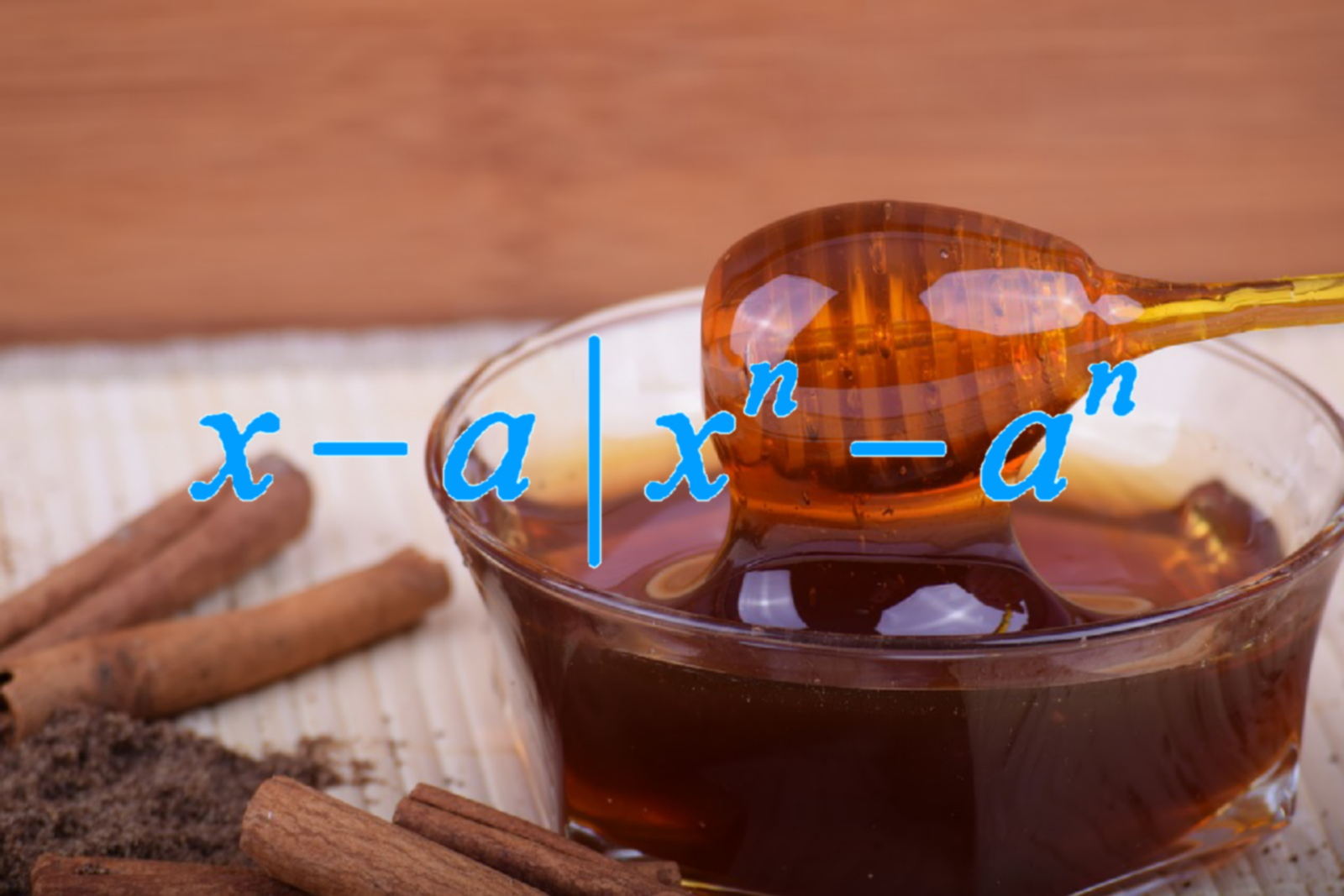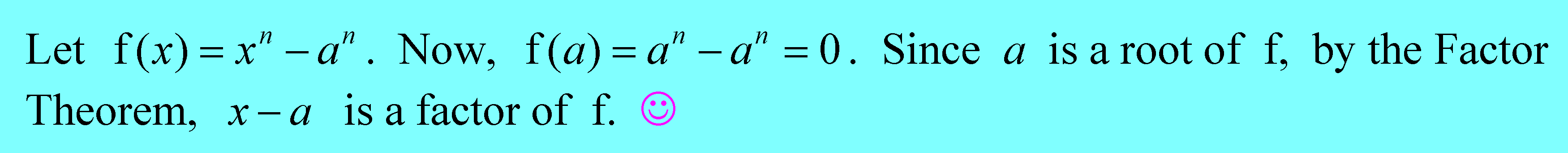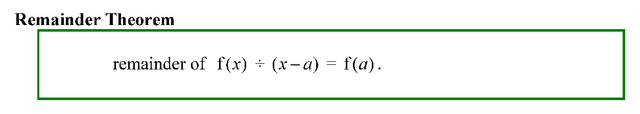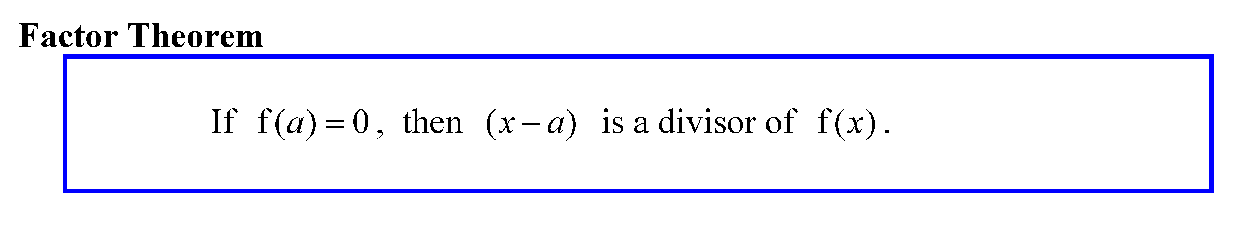A Short and Sweet Proof via Factor Theorem
The Succinct Proof
I chanced upon @mes's article on the proof that x - a is a factor of . He used k instead of n, but it is the same thing. Let me share with you a short and simple proof using the Factor Theorem, as follows.
Done! Complete! Finito!
Short and sweet proof, via the power of the Factor Theorem! This is like once you have the machinery set up. you press the button, and it works like magic! But how did we get the Factor Theorem? Let me give you a short tour of the machinery.
How does it work?
Let us start with what we know from primary / elementary school. We know that for whole numbers, we have, for example 17 ÷ 3 = 5 r 2. The quotient is 5 and the remainder is 2. We can always write the dividend (the original number to be divided) as dividend = divisor × quotient + remainder. In this example, we would write 17 = 3 × 5 + 2. Also notice that the remainder is always less than the divisor.
The polynomials behave in a similar fashion. Let us look at an example.
From the long division working, we know that when divided by
, the quotient is
and the remainder
. The remainder is of degree 1, whereas the divisor
has degree (highest power) 2. The degree of the remainder is less than that of the divisor.
Polynomial Theory
Once we get the quotient and the remainder, we can always write the dividend (the original polynomial to be divided) as dividend = divisor × quotient + remainder. Also, the degree of the remainder is always less than the degree of the divisor. These facts are true in general.
The Remainder and Factor Theorems
If the divisor is linear (degree 1), for example x - a, the remainder, being of a lesser degree, will be some constant. Suppose the dividend f(x) is divided by the divisor (x - a) to get some quotent Q(x) and some constant remainder R, then
f(x) = (x - a)·Q(x) + R.
Letting x = a, we get f(a) = 0·Q(a) + r = R. In other words, R = f(a). We do not need to worry about Q(a), because it is being multiplied by 0. Clever, eh? This is the Remainder Theorem.
The Remainder Theorem says that when you divide f(x) by (x - a), the remainder is always the same as that obtained if you substituted a into the x and crunched out the number. As an example, if you take f(x) = divided by (x - 2) via loooooooog division, you will get 3 as the remainder. However, if you substituted x = 2 into the formula f(x), you get f(2) =
= 8 - 5 = 3, the same answer straightaway!
This is POWERFUL! Or as we say, in Singapore, "POWDERFUL!".
So what about the Factor Theorem? Well, the Factor Theorem is just the Remainder Theorem when the remainder is zero.
Suppose you are considering the division of f(x) by (x - a). If you do that substution x = a to calculate f(a), and you get 0, that means the remainder is zero, and that would imply that the divisor (x - a) divides f(x) exactly. That is precisely because you have no remainder. Thus, (x - a) is a factor of f(x).
As an example, let us say f(x) = . Now f(2) =
= 8 - 8 = 0. 2 is a root of f(x)=0. Therefore x - 2 is a factor of
. And by the way, this is an example of the fact that
is a factor of
in general.
Mathematics is about beauty, simplicity and elegance. But to achieve that, we need a deeper understanding of how things work.
Image Credit
The first image was modified from Pixabay, while the rest are all my own work.
Announcements
You might also want to read my recent articles:
Two Squares in a Circle Problem
"Singapore Math" : The Cows and Goats Problem
Inequality: Always, sometimes or never?
If you find my articles useful or interesting, please upvote and resteem them! Thanks !
Cheers!!!
@tradersharpe
-- promoting sharp minds