Funciones: Nociones Fundamentales
Saludos a toda la comunidad científica y académica de Steemit, en esta oportunidad estaré presentando el inicio de una nueva temática como de costumbre, desde la perspectiva algebraica en su mayor parte, se trata de las Funciones. En esta entrega, de forma detallada y explicativa se mostrarán las nociones fundamentales del referido tópico de la Matemática, así como ejemplos concretos vinculados a la cotidianidad con lo cual se pretende dar cuenta de la aplicabilidad de este concepto en la realidad palpable. Es de hacer notar, que lo que se muestra tiene amplias ramificaciones por lo que se considera un tema de gran impacto y hasta una posible columna vertebral de la Matemática de la mano con los conjuntos numéricos.
A pesar de ser el inicio de una temática particular, es muy importante que se tenga en cuenta todo lo estudiado en las publicaciones precedentes, en tanto que son soporte teórico de gran importancia para lo que se mostrará a continuación. Debemos recordar que el conocimiento matemático no es aislado, todo está vinculado en una perfecta secuencia que va desde sus bases hasta los conceptos de alto nivel, razón por la cual nada es desestimable en esta área científica.
Los invito cordialmente a explorar los saberes que se presenta a continuación, desde una mirada reflexiva e integradora.
Antes de pasar a la formalidad matemática, considero necesario recordar el concepto de Relaciones Binarias, en particular cuando se hacía referencia al hecho de que
En la realidad humana es posible percibir relaciones entre todo lo que existe de acuerdo a cualidades, propiedades, condiciones, entre otros, que permiten al menos vincular dos situaciones, personas, animales, cosas; es típico en nuestra expresión verbal utilizar frases como
“es amigo de”, “es jefe de”, “vive en”, “obtuvo la calificación”, “su salario es”, “se desempeña en”, “su profesión es”, “se alimenta con”, “es novia de”, Fuente
A partir de esta visión se asume que existen cualidades con características específicas que permiten vincular elementos de la realidad, de allí que se precisaron como casos particulares dentro de este tema dos tipos de relaciones de gran impacto en el quehacer matemático:
- Relaciones de Equivalencia
- Relaciones de Orden
Ahora bien, existe otro tipo de Relación que trasciende el concepto mismo para convertirse en una noción de poderosa en el ámbito matemático, sin dejar de ser una relación, a saber, las Funciones, las cuales se procede a definir como sigue
- Funciones
La función o aplicación f es una relación que va desde un conjunto A al cual denominaremos conjunto de partida a un conjunto B al que llamaremos conjunto de llegada el cual además de verificar que f⊂A×B, cumple de manera estricta con las siguientes condiciones:
Existencia de Imagen: Esto indica que todo elemento del conjunto de partida tiene su correspondiente imagen en el conjunto de llegada, lo cual se expresa así
Lo anterior se lee: Para todo elemento del conjunto de partida existe un elemento en el conjunto de llegada tal que la imagen de los elementos del conjunto de partida a través de la función es igual a un elemento en el conjunto de llegada
Unicidad de Imagen: Todo elemento del conjunto de partida tiene una y sólo una imagen en el conjunto de llegada, esto se expresa
Lo mostrado establece que imágenes diferentes del conjunto de llegada provienen de elementos diferentes del conjunto de partida. También se puede decir que a elementos iguales del conjunto de partida le corresponden imágenes iguales en el conjunto de llegada como señala su contrarrecíproco representado como sigue
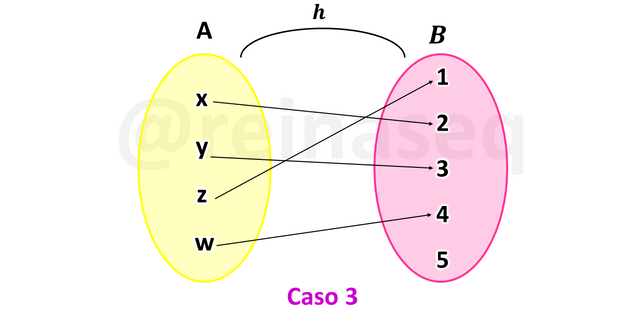
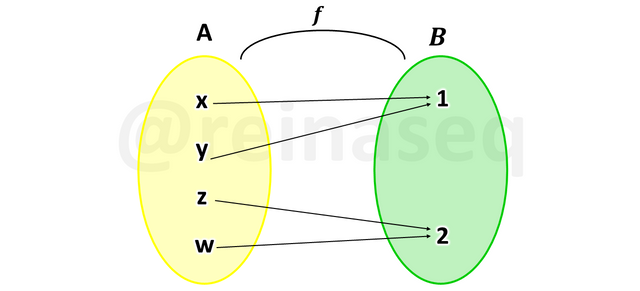
Para comprender la definición observemos las siguientes imágenes
En la misma observamos que la relación f no es función por cuanto no cumple con la existencia de imagen al tener al elemento b∈A que no posee imagen en el conjunto de llegada.
En cuanto a la relación g se evidencia que tampoco es función, ya que el elemento a∈A posee dos imágenes en el conjunto de llegada, lo cual indica que no se verifica la condición de unicidad de imagen
Al evaluar la relación h primeramente se observa que todos los elementos del conjunto de partida tienen imagen en el conjunto de llegada y al mismo tiempo es obvio que la imagen de cada elemento de A es única, por lo tanto se puede afirmar que h es función en tanto que cumple cabalmente con la definición.
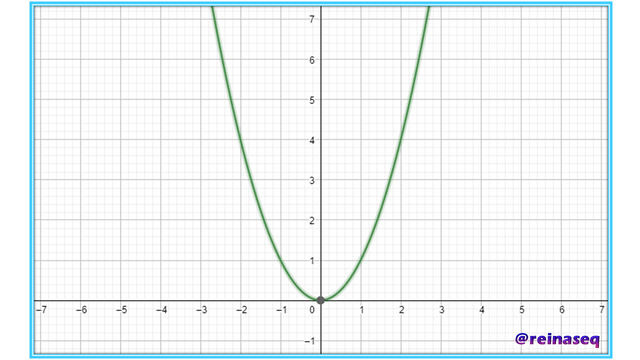
Las funciones tiene las mismas formas de representación gráfica que se utilizan para las relaciones binarias, no obstante, en el caso del Diagrama de Venn generalmente se utiliza para introducir y comprender los conceptos inherentes a las mismas mediante conjuntos finitos. En cuanto a la Representación Cartesiana es la más utilizada para la representación de funciones tanto en el plano como en el espacio. En este caso recordamos que si estamos en el plano, se acostumbra representar el conjunto de partida en el eje horizontal el cual se identifica con una x y se le llama eje de las abscisas y el conjunto de llegada estará en el eje vertical el cual se identifica con una y y se le denomina eje de las ordenadas. A continuación se muestran las siguientes gráficas a manera de ejemplo
Antes de seguir avanzando es importante destacar las siguientes precisiones:
- Toda función es una relación pero no toda relación es una función
- La función o cualidad que permite vincular los elementos del conjunto de partida con los elementos del conjunto de llegada se denota f, g, h,…, y la forma de representar la imagen de los elementos del conjunto de partida a través de la función se expresa f(x), g(x), h(x),…, notaciones que deben tener muy claras evitando correr el riesgo de confusión, por cuanto es habitual observar en algunos materiales didácticos o textos como se indica erróneamente que f(x) es función cuando en realidad se trata de una imagen.
En caso de que exista el riesgo de ambigüedad se recomienda lo siguiente:
- Si se trata de plantear un ejercicio o problema en el cual se deba estudiar el Dominio o Imagen o Rango de la función se recomienda utilizar la siguiente expresión o similar:
Dada la función definida por f(x)=y
- En caso de que no sea el Dominio o Imagen o Rango lo que se va a estudiar sino por ejemplo casos relativos al Límite, Derivada o Integral se recomienda plantear en los problemas o ejercicios las funciones de la siguiente forma
Dada la función f:A→B/f(x)=y
Recordemos que en Matemática la formalidad es fundamental y la misma no debe obviarse por la premura de los cálculos, hacer es lo que generalmente se conoce como abusos del lenguaje matemático.
- Dominio y Rango
Para el caso de las funciones estos conceptos se definen de manera de similar salvo las siguientes precisiones:
En cuanto al Dominio de una Función es claro por la condición de existencia de imagen que el mismo coincide exactamente con el conjunto de partida, por lo cual la definición se expresa como sigue
Dada la función f⊂A×B se tiene que
Por otro lado, el conjunto Imagen o Rango de la Función se mantiene de forma similar a las relaciones binarias por cuanto no se amerita que el rango deba coincidir con el conjunto de llegada para ser función, no obstante, en caso de haber coincidencia la función adopta una cualidad adicional que conoceremos más adelante. Luego la expresión matemática para el Rango de la Función es la siguiente
En el ámbito de las funciones se distinguen ciertas funciones que se consideran especiales o notables por sus características propias, a continuación se presentan una a una.
- Funciones Constante
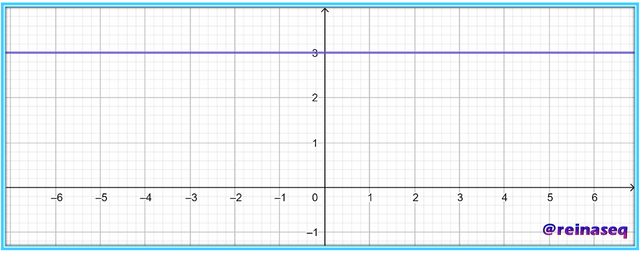
Se trata de la función que asigna como imagen a cada elemento del conjunto de partida un valor constante k, la cual se denota simbólicamente de la siguiente manera
Como ejemplo gráfico se muestra el siguiente
- Funciones Identidad
Esta función asigna a cada elemento del conjunto de partida el mismo elemento, esto quiere decir que no los modifica. En este sentido, la función identidad es una función neutra, la cual se denota como iA y su definición matemática es la siguiente
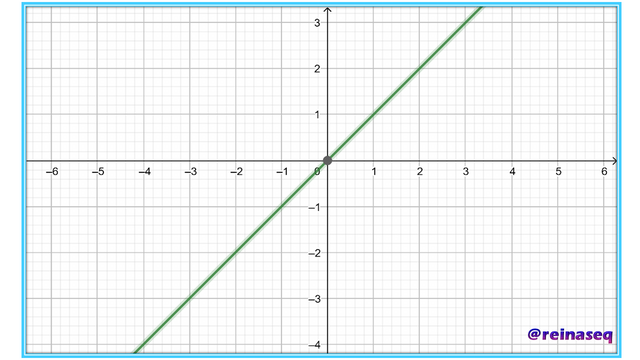
Su representación gráfica es la siguiente
Al realizar su estudio como relación nos damos cuenta que cumple con las definiciones de relación de equivalencia y relación de orden amplio. Asimismo representa la Diagonal del producto cartesiano A×A.
- Función Proyección
Son funciones que se proyectan en el producto cartesiano A×B de acuerdo a las siguientes expresiones
Como puede observarse, la función proyección asigna la primera o segunda componente del par ordenado respectivamente.
- Función Canónica
Para esta función se debe considerar una relación de equivalencia ~ definida en A≠∅, recordemos que por el Teorema Fundamental de las Relaciones de Equivalencia - ver aquí - al definir una relación de equivalencia en un conjunto no vacío, la misma genera una partición en clases de equivalencia disjuntas entre sí, las cuales son elementos del conjunto cociente A⁄∼.
En este sentido, se define la función canónica como una aplicación que va desde el conjunto A≠∅ hacia el conjunto cociente A⁄∼ de tal manera que a cada elemento del conjunto de partida le asigna una clase de equivalencia en el conjunto de llegada. Simbólicamente tenemos
Esto quiere decir que si dos elementos están relacionados admiten la misma imagen, esto es
Una vez que hemos logrado comprobar que una determinada relación es una función es el momento de conocer que tipo es. En este orden de ideas, de acuerdo a ciertas condiciones o cualidades se distinguen las siguientes
- Función Inyectiva
- Función Sobreyectiva
- Función Biyectiva
A continuación, conozcamos en detalle cada una de sus peculiaridades.
- Función Inyectiva
La inyectividad ocurre cuando a elementos diferentes del Dominio de f le corresponden imágenes distintas. También puede decirse que sucede cuando imágenes iguales provienen de elementos iguales del conjunto de partida. Adicionalmente, es común que a una función Inyectiva también se le denomine biunívoca o función 1-1. Expresado en símbolos
O mediante su contrarrecíproco
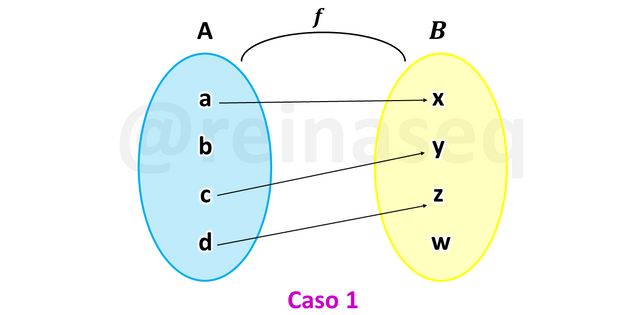
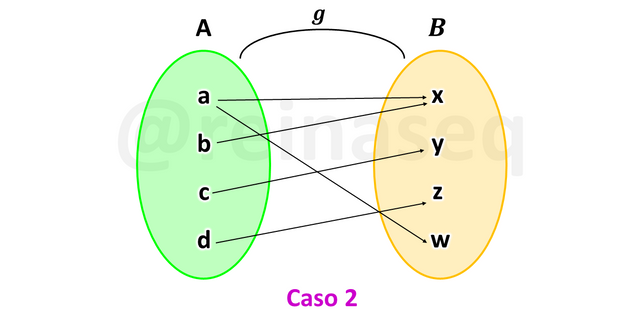
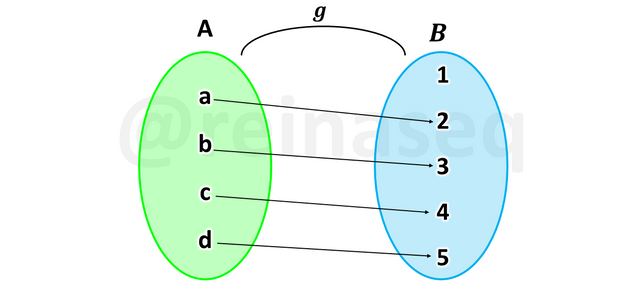
Observemos las siguientes imágenes
Como se puede apreciar la función f no es Inyectiva en tanto que se puede evidenciar que hay imágenes que provienen de elementos diferentes, esto conlleva a afirmar que no se cumple la definición de inyectividad. Si lo analizamos desde la otra perspectiva, nos damos cuenta de que hay elementos diferentes del Dominio de f que poseen la misma imagen en el conjunto de llegada, hecho que ratifica el no cumplimiento de la condición.
En cuanto a la función g se puede apreciar con claridad que cumple con la definición de inyectividad, luego se puede concluir que g es Inyectiva.
Es importante tener la precaución de no confundir la inyectividad con la condición de unicidad de imagen debido a la similitud que presentan las mismas, mientras que existen funciones que obviamente por serlo verifican la unicidad de imagen no necesariamente son inyectivas, como se evidencia en el ejemplo anterior en cuanto a la función f.
- Función Sobreyectiva
También conocida como función sobre, epiyectiva, suprayectiva o subyectiva se trata de una condición en la cual en una función el conjunto Imagen o Rango coincide exactamente con el conjunto de llegada, esto quiere decir, que todo elemento del conjunto de llegada es imagen de algún elemento del conjunto de partida. Su representación simbólica es
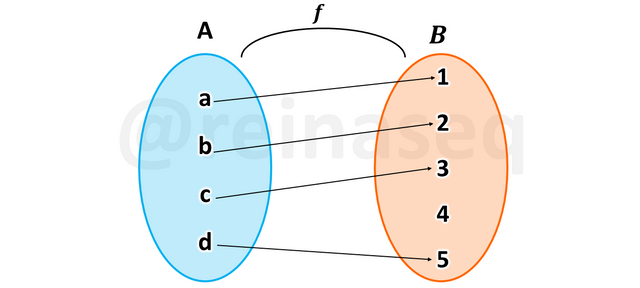
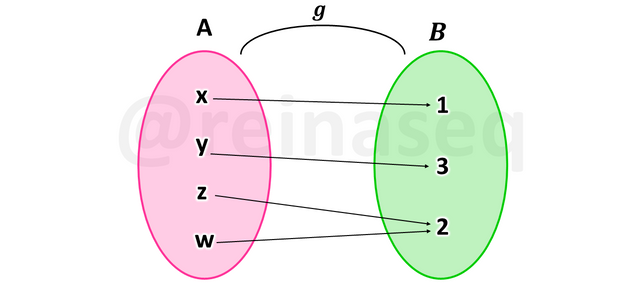
Es de hacer notar que esta definición se suele confundir con la condición de existencia de imagen, no obstante es sencillo diferenciarlas en tanto que en la condición de existencia de imagen se trata de que todos los elementos del conjunto de partida tengan imagen en el conjunto de llegada y la sobreyectividad nos indica que todos los elementos del conjunto de llegada tengan preimagen en el conjunto de partida. Asimismo, conviene tener presente que el cumplimiento o no de esta propiedad es independiente pero no excluyente del cumplimiento de la inyectividad. En las siguientes imágenes se pueden observar las posibilidades de que se verifique o no esta definición.
En el caso de la función f es visible que a pesar de que se cumple la inyectividad no se verifica la sobreyectividad por cuanto el elemento 4∈B no tiene preimagen, por lo cual no se cumple la definición.
La función g por el contrario no verifica la inyectividad, sin embargo, nos damos cuenta de que todo elemento del conjunto de llegada tiene su respectiva preimagen en el conjunto de partida, por lo tanto g es sobreyectiva.
- Función Biyectiva
Las funciones serán biyectivas si de manera simultánea cumplen con la inyectividad y la sobreyectividad. Puede ocurrir que se cumpla al menos una de ellas, en ese caso no se puede concluir la biyectividad, en los ejemplos gráficos planteados para la propiedad anterior es claro que ni la función f ni la función g cumplen con esta definición.
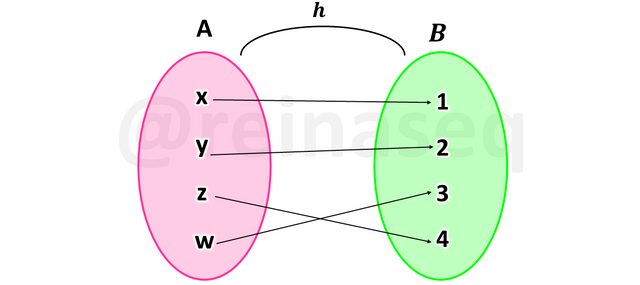
Visualicemos la imagen a continuación
Es claro que la función h es inyectiva y sobreyectiva, luego se puede concluir que h es biyectiva.
A continuación se plantean dos problemas cotidianos en los cuales es posible apoyarse en el concepto de funciones para conseguir respuestas y predicciones para la mejor toma de decisiones:
- Ejemplo 1
Se estima que en un campo de 470 árboles de naranjos se producirá 34.700 naranjas. Suponiendo que todos los árboles producen la misma cantidad de frutos, determinar:
- La función que proporciona el número total de naranjas en función del número de árboles de naranjos. ¿Qué tipo de función es? Representa su gráfica.
- ¿Cuántas naranjas se producirían en total si se plantan 150 naranjos adicionales?
- ¿Cuántos árboles de naranjos se necesitan para producir un mínimo de 74.000 naranjas?
Solución
- Para dar respuesta al primer planteamiento, procedemos mediante el siguiente razonamiento deductivo:
Para conocer en promedio cuantas naranjas produce cada árbol de naranjo basta con dividir la producción total prevista entre el número total de árboles de naranjos como sigue
34700/470=73,82978723…
Si redondeamos se considera que aproximadamente cada árbol de naranjo dará una producción de 74 naranjas. Luego la función que proporciona el número total de naranjas viene definida por la expresión f(x)=74x, lo que indica que estamos en presencia de una función lineal o afín. Gráficamente su representación es la siguiente
- En cuanto a la segunda solicitud, primeramente se debe precisar mediante una adición el total entre la cantidad de árboles de naranjos que se tienen, más los adicionales que se aspiran plantar. Esto es
470+150=620
Luego, lo que se solicita en realidad es la imagen del elemento 620 a través de la función f definida por f(x)=74x como sigue
f(620)=74×620
f(620)=45880
Por lo tanto el número de naranjas se producirán en total al plantar 150 árboles de naranjos adicionales es 45880.
- En relación a la tercera solicitud procederemos de la siguiente forma:
Se pide determinar el número de árboles de naranjos necesarios para producir como mínimo de 74.000 naranjas, lo cual nos plantea el siguiente escenario
f(x)≥74000
Esto implica que
74x≥74000
Por definición de la relación de orden ≥ tenemos lo siguiente

Para precisar el valor solicitado consideramos 74x=74000
Al resolver la ecuación tenemos que x=1000
Este valor nos indica que se deben sembrar como mínimo 1000 árboles de naranjos para obtener como producción esperada 74000 naranjas.
- Ejemplo 2
María desea adquirir un Smartphone y para ello evalúa los precios ofertados de dos compañías proveedoras de bienes y servicios relacionados con la telefonía móvil:
La compañía 1 le plantea cancelar 0,5 Bs. S por establecer cada llamada y 0,25 Bs. S por cada minuto de duración de la llamada.
La compañía 2 le plantea cancelar 0,3 Bs. S por establecer cada llamada y 0,3 Bs. S por cada minuto de duración de la llamada.
Se requiere:
- Representar la función del costo de una llamada en cada una de las compañías.
- Calcular cuándo es más recomendable una compañía u otra en función del tiempo de duración de una llamada.
- María generalmente realiza 74 llamadas mensuales que suman un total de 470 minutos. ¿Cuál de las dos compañías le conviene contratar?
Solución
- Para dar respuesta a la primera solicitud considerando la información suministrada en el problema para cada una de las compañías, conlleva a que las funciones estarían definidas por las siguientes expresiones:
Compañía 1: f(x)=0,5+0,25x, ∀x≥0
Compañía 2: g(x)=0,3 +0,3x, ∀x≥0
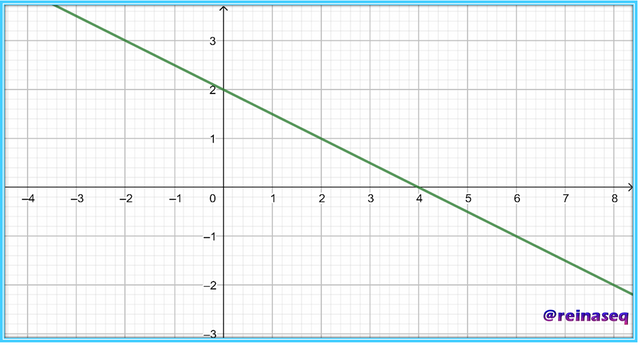
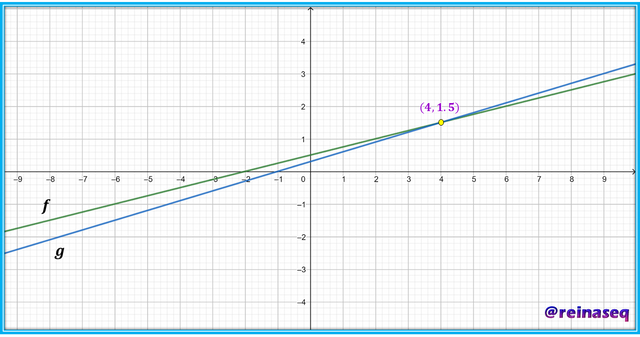
Graficando f y g tenemos
De acuerdo a la imagen f y g se intersectan cuando x=4 por lo cual conviene evaluar ambas funciones para ese valor
f(x)=0,5+0,25(4)
Luego f(x)=1,5
g(x)=0,3 +0,3(4)
Luego g(x)=1,5
Como se esperaba en ese punto (4 minutos de duración de la llamada) el valor de la misma es idéntico. Guiándonos por el gráfico y considerando el tiempo de duración de las llamadas de María debería decidir entre los siguientes escenarios:
Si las llamadas duran menos de 4 minutos le conviene adquirir los servicios de la compañía 2.
Si las llamadas duran más de 4 minutos le conviene adquirir los servicios de la compañía 1.
Para dar respuesta al tercer requerimiento del problema, basta con escalar cada una de las expresiones matemáticas que definen a las funciones f y g, en tanto que las mismas describen el comportamiento para una sola llamada. Adicionalmente se evalúa el valor de x=470 en ambos casos recordando que es el número total de minutos de duración de las llamadas de María. Procedamos:
Compañía 1:
f(x)=0,5.(74)+0,25.(470)
Luego, resolviendo las operaciones matemáticas involucradas tenemos que
f(x)=154,5
Compañía 2:
g(x)=0,3.(74) +0,3.(470)
Luego, resolviendo las operaciones matemáticas implicadas se tiene que
g(x)=163,2
De acuerdo a los valores obtenidos, el costo total del servicio en la compañía 1 es de 154,5 Bs. S y en la compañía 2 es de 163,2 Bs. S., por lo tanto, la mejor opción para María es contratar los servicios de la compañía 1.
En esta oportunidad hemos comenzado a estudiar las nociones fundamentales del concepto de función, enfatizando y explicando minuciosa y detalladamente los diferentes aspectos inherentes al mismo, paseándonos desde la máxima comprensión de su definición formal, reconociendo las particularidades en cuanto a sus formas de representación gráfica, dominio y rango, resaltando las cualidades de ciertas funciones especiales o notables, hasta llegar a su clasificación, de acuerdo a las definiciones de inyectividad, sobreyectividad y biyectividad. Posteriormente, se presentaron dos ejemplos donde se evidencia la aplicación de las funciones en casos concretos de la cotidianidad de los seres humanos.
Las funciones tienen un gran uso en los diferentes aspectos de la vida de los individuos y en diferentes áreas del conocimiento, por lo general cuando se están conociendo es común partir de las expresiones matemáticas que las definen, pero de igual modo pasando de procedimientos matemáticos simples hasta otros más avanzados y de nivel, es posible tomar datos de la realidad y determinar la representación algebraica que definen funciones de esos hechos.
En las próximas publicaciones, desde la perspectiva algebraica seguiremos estudiando otros saberes matemáticos implicados en el concepto de función, nos leemos en el siguiente post, saludos y éxitos para todos los lectores y académicos de esta comunidad.

La Matemática nos ayuda a comprender la realidad representando y prediciendo situaciones inherentes al quehacer humano – Reina Sequera
La Matemática nos ayuda a comprender la realidad representando y prediciendo situaciones inherentes al quehacer humano – Reina Sequera

Referencia
Armando, R. (2001). Algebra I. Edición XX. Editorial El Ateneo.
Lipschutz, S. (1970). Teoría de Conjuntos y Temas Afines. Teoría y 530 problemas resueltos. Serie de compendios SCHAUM. Mc Graw-Hill.
Todas las imágenes, separadores y banners de este artículo son de autoría propia diseñadas en el editor de presentaciones Microsoft Powerpoint 2013, ajustadas y recortadas en Paint.
Los ejemplos fueron consultados en Fuente y adaptados por @reinaseq
Los gráficos cartesianos fueron diseñados por @reinaseq mediante el software Geogebra en Línea
Publicación Anterior
Si estás interesado en contenidos sobre Ciencia, Tecnología, Ingeniería y Matemática, consulta las etiquetas #STEM-Espanol y #SteemSTEM, las cuales puedes utilizar para realizar tus publicaciones en esas áreas. Puedes unirte al servidor de Discord de STEM-Espanol para participar en nuestra comunidad y consultar los reportes semanales publicados por @STEM-Espanol. Te esperamos!!
Si estás interesado en contenidos sobre Ciencia, Tecnología, Ingeniería y Matemática, consulta las etiquetas #STEM-Espanol y #SteemSTEM, las cuales puedes utilizar para realizar tus publicaciones en esas áreas. Puedes unirte al servidor de Discord de STEM-Espanol para participar en nuestra comunidad y consultar los reportes semanales publicados por @STEM-Espanol. Te esperamos!!
- Normas STEM-Espanol
- Directrices sobre normas de derechos de autor
- Servidor Discord #STEM-Espanol
- Para unirte al trail de STEM-Espanol
- Vota por @stem.witness como Testigo aquí







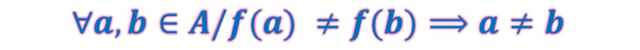
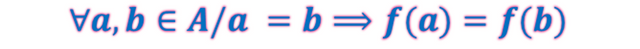

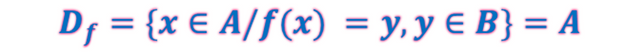
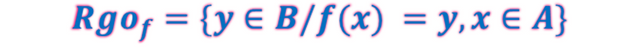

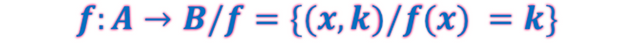
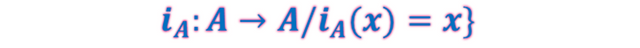
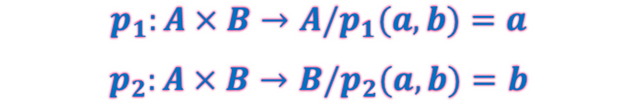
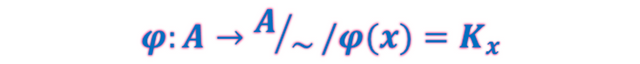
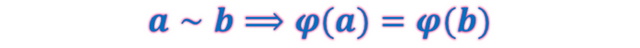






Congratulations! This post has been upvoted from the communal account, @minnowsupport, by reinaseq from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Muy interesante aporte me gusto la información plasmada en la comunidad Steemit un saludo.
Votado por el trail @team-mexico
Canal Discord ¡Te esperamos!
Delegaciones para @team-mexico ¡Ayúdanos a crecer!
10 SP - 25 SP - 50 SP - 100 SP - 150 SP- Mas información.
.png)
Hola, este post ha sido propuesto para ser votado por Cervantes. Saludos.
Muy didáctico tu post, estimada @ReinaSeq. He recapitulado algunas cosas leyéndolo. Es un tema esencial. Veo también que conseguiste una forma de denotar las expresiones, usando cursivas o negritas. Se ve bien 😃 Saludos.
Hola @eniolw, las bases son muy importantes y siempre hay que tenerlas presente! Me alegra que haya servido de repaso!! En cuanto a las expresiones matemáticas si me parece útil la cursiva o negrita mientras que Steemit amplia sus posibilidades en cuanto al lenguaje algebraico!! Muchas gracias por el seguimiento y los aportes!! Saludos!!
Congratulations @reinaseq! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Buen post!