En esta oportunidad quiero dar un especial saludo a las comunidades de #stem-spanol, #cervantes, #proconocimiento y #entropia, por su valioso apoyo a las publicaciones de habla hispana orientadas al contenido científico y académico, en donde se valora el aporte en las ramas de matemática, química, física, biología, ingeniería y educación. En esta ocasión quiero explicar todo lo concerniente al análisis y estudio de los ritmos o velocidades de cambio mediante el uso y aplicación de la derivada.

Como he mencionado en artículos anteriores, la derivada nace de una necesidad física, es decir en la antigüedad se venía estudiando el problema de la recta tangente debido a la necesidad de dar respuestas a los ritmos y velocidades de cambio, es por ello que no existe mejor manera de entender los cambios de velocidad que mediante el uso de la derivada.

En el articulo referente a estudio del cálculo: la derivada y el problema de la recta tangente, tuve la oportunidad de hacerles referencia acerca de que la derivada se utiliza para para calcular pendientes, teniendo en cuenta lo que voy a explicar en esta publicación puedo argumentar que la derivada no solamente nos proporciona las herramientas necesarias para calcular la pendiente de la recta tangente a una función, sino que también podemos determinar el ritmo de cambio de una variable con respecto a otra, lo que le da la bondad a la derivada de poseer una utilidad en una amplia variedad de situaciones, en las que se encuentra también los cambios de velocidad.

Los ritmos de cambios que expresa nuestra noble naturaleza son infinitos en su variedad, todo depende en el área de estudio que estos ocurran, sin embargo puedo mencionar algunos ritmos de cambios que suelen darse en diferentes áreas del saber científico y experimental, estos son:

• Crecimiento poblacional.
• Ritmos de reproducción.
• Caudal de fluido.
• Velocidad y aceleración de un objeto.

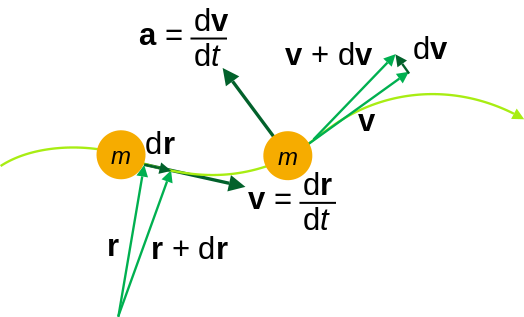
Fuente de imagen. Wikimedia Commons. Dominio público

Un uso frecuente de los ritmos de cambio es tener que describir el tipo de movimiento, por ejemplo si el movimiento de la variación es graficado en el sistema cartesiano y describe una línea recta, entonces esta recta se suele representar en posición horizontal o vertical, con un origen marcado en ella. Sobre tales rectas, el movimiento hacia la derecha o hacia arriba se considera de dirección positiva, y el movimiento hacia la izquierda o hacia abajo de dirección negativa.

Otra de la característica de este fenómeno de ritmos de cambio es que la función sque representa la posición (respecto al origen) de un objeto como función del tiempo t se denomina función (de) posición, en el que cierto lapso de tiempo ∆t el objeto cambia su posición en una cantidad ∆s = s(t+∆t) -s(t), por lo que podemos emplear las siguientes fórmulas:

• Razón= distancia/tiempo
• (Cambio en distancia / Cambio en tiempo) = ∆s/ ∆t , este fórmula es comúnmente conocida como velocidad media.

Ejemplo de velocidad media de un objeto en su caída

Si se deja caer una pelota de béisbol desde una altura de 100 metros, su altura s en el instante t se representa mediante la función posición

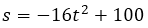
donde s se mide en metros y t en segundos.

Fuente de imagen. Wikimedia Commons. Autor: MichaelMaggs. Bajo Licencia Creative Commons Attribution-Share Alike 3.0 Unported

Encuentre la velocidad media para el intervalo de tiempo de [1,2] segundos.

La solución del ejercicio radica en analizar la ecuación para el calculo de la velocidad media, si la velocidad media es el cociente entre la variación del cambio de posición y el cambio del tiempo, entonces tenemos que la velocidad media (∆s/ ∆t), se puede interpretar como sigue:

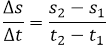
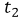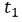• Para el intervalo de tiempo [1,2] se puede decir que = 2 y = 1.

• Para conseguir 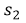y 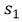se sustituye el valor del intervalo de tiempo en la función 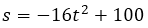, por lo que:

→

→

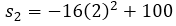
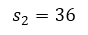
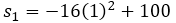
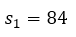
• Ya teniendo la variación del tiempo y la variación de la posición, solo nos queda sustituir en la fórmula de velocidad media:

→

→

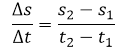
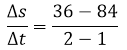
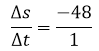
Si s se mide en metros y t en segundos entonces la velocidad media de la pelota de béisbol que se dejó caer desde la altura de 100 metros en el intervalo de tiempo de [1,2] segundos llevaba una velocidad de 48 metros por cada segundo. El que el resultado del ejercicio haya dado negativo significa que la pelota viene bajando.

Para este caso en particular de la velocidad media, es decir en el caso específico que se conoce un intervalo de tiempo no es necesario el uso de la derivada ya que la pendiente se puede calcular fácilmente con la fórmula 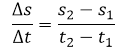, posteriormente analizaremos el caso de la velocidad instantanea, en donde solo se conoce un punto, es decir a un instante de tiempo, para ese caso en particular si es necesraio emplear el uso de la derivada.

Aplicación de la derivada para el cálculo de la velocidad instantánea

En general si s= s(t) es la función posición de un objeto en movimiento rectilíneo, su velocidad en el instante t viene dado por la siguiente expresión:

=

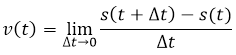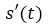
Con lo que podemos concluir que el cálculo de la velocidad instantánea se encuentra con la derivada de la función s(t).

Veamos el siguiente ejercicio de una aplicación de la derivada para el cálculo de la velocidad instantánea:

En el instante t=0, se lanza un proyectil desde una altura de 15 metros. La posición del proyectil está dada por:

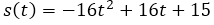
Fuente de imagen. Wikimedia Commons. Licencia Creative Commons Attribution-Share Alike 3.0 Unported

Encuentre:
a. ¿cuánto tarda el proyectil en llegar al suelo?
b. ¿Cuál es su velocidad al momento del impacto?

La solución de este problema se resuelve fácilmente, solamente tenemos que encontrar la derivada de la función .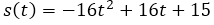

Para encontrar el tiempo que tarda el proyectil en llegar al suelo igualamos la función 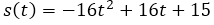a cero, y como la función es de segundo grado nos va a arrojar dos soluciones, un 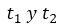. Para conseguir la velocidad con que el proyectil llegó al suelo, es necesario sustituir el instante de tiempo de mayor valor en la derivada de la función .

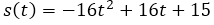Para simplificar la derivada de la función posición, realizamos la derivada aplicando las reglas básicas de derivación. Por lo que:

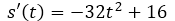
Ya obtenida la derivada, solo falta conseguir los instantes de tiempo, para ello tomamos la función 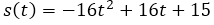y la igualamos a cero y encontramos los valores de t.

→

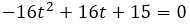
Para resolver esta ecuación de segundo grado aplicamos la ecuación de la resolvente de segundo grado.

=

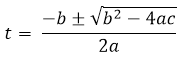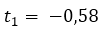
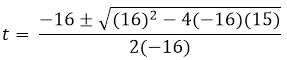
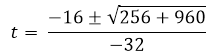
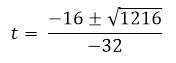
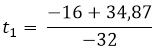
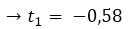
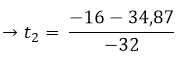
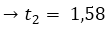
El tiempo que se tarda el proyectil en llegar al suelo es de 1,58 segundos. Para encontrar la velocidad con la que llego al suelo basta con sustituir el tiempo de 1,58 segundos en la derivada de la posición.

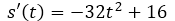
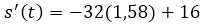
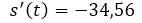
La velocidad de impacto del proyectil con el suelo es de 34, 56 m/s. El negativo de la velocidad significa que el objeto viene bajando.

Conclusiones

1. En todo fenómeno que nuestra naturaleza presenta, en el que podemos apreciar como una variable cambia con respecto a otra, estamos en la presencia de ritmos o velocidades de cambio, en los que suele ser de gran utilidad la aplicación de la derivada.

2. Más que poder aplicar la derivada es muy importante la interpretación de las funciones que rigen el comportamiento de cambio, ya que de su interpretación dependerá la facilidad con la que podamos plantear la derivada con la que vamos encontrar la variación de ese ritmo de cambio.

3. En el caso particular de esta publicación tratamos dos casos en específico, que son la velocidad promedio y la velocidad instantánea, aunque la aplicación de ritmos de cambio se puede extender inclusive para cálculos de caudal de flujo, variación en la viscosidad de un fluido, en fin para cualquier variable que cambie generalmente con respecto al tiempo.

4. En el caso de los alumnos a nivel universitario resulta de mucha motivación para ellos, el poder visualizar muchas de las aplicaciones que la derivada tiene con respecto al fenómeno de la variante de los ritmos o velocidades de cambio.

Referencias bibliográficas consultadas

• Cálculo con Geometría analítica. Autor: Ron Larson y Robert P. Hostetler. 8va edición. Editorial Mc Graw Hill. Volumen I. México 2006.

• El Cálculo. Autor: Louis Leithold. 7ma edición. Editorial Oxford. México 1998.

---

"Para toda aquella persona que le apasiona la matemática, física, química, biología, educación e ingeniería, le recomiendo la etiqueta de #stem-spanol, es una comunidad que valora el contenido intelectual y académico de calidad, conservando siempre la originalidad de las publicaciones, por lo que se recomienda a todos aquellos amigos de steemit que deseen publicar utilizando esta etiqueta a no cometer plagio."