Sistema de dos ecuaciones de 1er grado con dos incógnitas - GMath

Saludos amigos y lectores de mi blog, bienvenidos, en esta nueva entrega que compartiré con ustedes, hablaré un poco de los sistemas de ecuaciones de ecuaciones de 1er grado, con dos incógnitas, los métodos para resolverlas y como podemos clasificar dichos sistemas. Este tema además de ser sencillo, es muy práctico e importante que deben dominar los estudiantes, ya que forma parte importante en un curso de Matemáticas Básicas o Pre-Universitaria. Espero que puedan comprender el tema que abordamos en está publicación. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin quitarles más tiempo en la lectura previa, empecemos a trabajar un poco.

---

Sistema de dos ecuaciones de 1er grado con dos incógnitas

Un sistema de dos ecuaciones de 1er grado con dos incógnitas, es un conjunto de dos ecuaciones de 1er grado descrito de la forma siguiente:

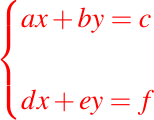
_{Imagen elaborada por @abdulmath, diseñadas y editada con y GIMP.}
donde a, b, c, d, e, f son números reales arbitrarios.

Diremos que (s,t) es una solución del sistema si satisfacen cada una de las ecuaciones del sistema dado. Una interpretación geométrica a este sistema, es que cada una de estas ecuaciones corresponde a una línea recta. Las preguntas que surgen en forma natural son: ¿tiene este sistema varias soluciones y, de ser así, cuántas?

El sistema de ecuaciones se llama:

• determinado, si éste tiene una solución única;
• imcompatible, en el caso contrario, es decir, cuando éste no tiene soluciones;
• indeterminado, si éste tiene más de una solución.

Los métodos más comunes utilizados para resolver tales sistemas son:

• método de sustitución,
• método de igualación,
• método de eliminación,
• método de Cramer.

La analogía entre las resoluciones analíticas y geométricas del sistema de dos ecuaciones de 1er grado con dos incógnitas es la siguiente:

---

En Geométria	En Álgebra
las lineas se intersecan	el sistema es determinado
las rectas son paralelas y distintas	el sistema es imcompatible
las rectas coinciden	el sistema es indeterminado

---

Las cuales también podemos ver en la siguiente gráfica

_{Imagen elaborada por @abdulmath, diseñadas y editada con y GIMP.}

---

Ejemplo 01: (Sistema con una solución única) Considere el sistema

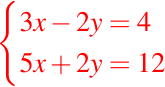
_{Imagen elaborada por @abdulmath, diseñadas y editada con y GIMP.}
Si usamos el método de eliminación, al sumar las dos ecuaciones obtenemos:


_{Imagen elaborada por @abdulmath, diseñadas y editada con y GIMP.}
Luego, sustituyendo este valor en la segunda ecuación y despejando y se tiene:


_{Imagen elaborada por @abdulmath, diseñadas y editada con y GIMP.}

Así, x=2 y y=1, satisfacen el sistema, por lo tanto debido a la manera en que se hallo la solución nos muestra que es el único par de números que satisfacen el sistema, es decir, el sistema tiene una única solución.

---

Ahora si procedemos a resolver el sistema de manera formal tenemos lo siguiente:

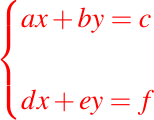
_{Imagen elaborada por @abdulmath, diseñadas y editada con y GIMP.}

Se deben analizar los siguientes casos:

• Caso 01:

  Si , el sistema solo tiene una incógnita, que es x.

• Caso 02:

  Si , el sistema solo tiene una incógnita, que es y.

• Caso 03:

  Si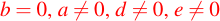 , entonces
  
  
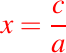
  luego y se puede usar la segunda ecuación para despejar y.

• Caso 04:

  Si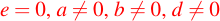 , entonces
  
  
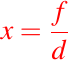
  luego se puede usar la primera ecuación para despejar y.

• Caso 05:

  Si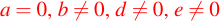 , entonces
  
  
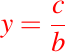
  luego se puede usar la segunda ecuación para despejar x.

• Caso 06:

  Si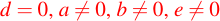 , entonces
  
  
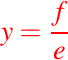
  luego se puede usar la primera ecuación para despejar x.

• Caso 07:

  Para este caso, es necesario hacerlo con mayor detalle, así que consideremos que los coeficientes .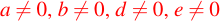

Si multiplicamos la primera ecuación por e y la segunda por b obtenemos

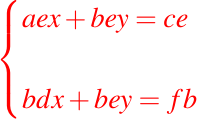
_{Imagen elaborada por @abdulmath, diseñadas y editada con y GIMP.}

Es de hacer notar que los sistemas descritos anteriormente son equivalentes, es decir, que cualquier solución del primer sistema es una solución del segundo sistema y viceversa.

Luego, si en el sistema anterior restamos las dos ecuaciones en el siguiente orden la primera menos la segunda, nos queda

_{Imagen elaborada por @abdulmath, diseñadas y editada con y GIMP.}

Note que si , entonces se puede dividir entre este término para obtener

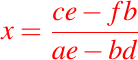
_{Imagen elaborada por @abdulmath, diseñadas y editada con y GIMP.}
Así, se puede sustituir este valor encontrado de x en el sistema inicial para despejar y, de esa manera hemos hallado una solución única del sistema.

---

Queridos amigos y lectores, espero hayan disfrutado leyendo y estudiando esta publicación, los espero en una próxima entrega donde seguiré trantando algunos puntos de desarrollo de matemáticas básicas, para así, además de compartir con ustedes mi experiencia, pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco mas del maravilloso mundo de las matemáticas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias.

• Baldor, J. Aurelio. Álgebra Elemental. Cultural Centroamericana, 1972.
• Baldor, J. Aurelio. Aritmética. Cultural Centroamericana, 1978.

---

También los invito a leer mis otras publicaciones que puedan ser de su interés:

• El triángulo de Pascal y los productos notables.
• Resolución de Ecuaciones e Inecuaciones lineales de 1er orden con una incógnita.
• Resolución de una ecuación de 2do grado con una incógnita.
• Otras consideraciones de la ecuación de 2do grado con una incógnita.
• Resolución de inecuaciones de 2do grado con una incógnita en el conjunto de los números reales.

---

Todas las imágenes son propias, creadas y editadas con software libre: , Karbon, Inkscape y GIMP.

_{Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.}