ANÁLISIS DESDE EL ENFOQUE DE LA INGENIERÍA SISMORESISTENTE DE LAS ZONAS DE UN ESPECTRO DE RESPUESTA ELÁSTICO, BASADO EN LAS PROPIEDADES DINÁMICAS DE SISTEMAS ESTRUCTURALES DE UN GRADO DE LIBERTAD: “Tn” Y “ξ”. PARTE I
Saludos apreciados lectores de #steemit, y muy especialmente a los que hacen vida en la comunidad científica de #stem-espanol, donde me siento honrado de ser el colaborador del sub-canal de discord de ingeniería. Me apasiona escribir sobre temas afines, asociados a mis áreas de especialización, siendo una de ellas la ingeniería sismoresistente. Si deseas interactuar más con nosotros comparto con ustedes el siguiente link del canal de discord de stem-espanol: https://discord.gg/huRbpp. Sin más preámbulos, espero disfruten del post:
INTRODUCCIÓN
El análisis espectral en el campo de la ingeniería sismoresistente constituye en definitiva uno de los grandes aportes de las matemáticas y la dinámica estructural, dado que los espectros son una excelente herramienta para la comprensión de la respuesta de una estructura ante la excitación del terreno (por ejemplo la causada por un sismo), cuyo proceso de construcción obedece a las propiedades dinámicas de esta, y la función que rige la excitación anteriormente comentada, que para el caso de interés está representada por un acelerograma; estos espectros así construidos se conocen como espectros de respuesta, sobre los cuales se inició el proceso de estudio en la referencia N°03, por lo que te invito amigo lector a que la consultes, para dar paso a una mayor comprensión de este tema; sin embargo, veo pertinente a modo de introducción hacer un breve resumen de la misma.
En este sentido, en la referencia N°03, aprendimos a construir un espectro de respuesta para un sistema que se comporta elásticamente, planteando la ecuación diferencial de equilibrio dinámico de forma alternativa (ver imagen N°01), y resolviéndola para distintos valores de período natural “Tn” y una fracción de amortiguamiento crítico “ξ”, utilizando para este fin la herramienta computacional NONLIN V 7.14, obteniendo a modo de respuesta, los desplazamientos máximo relativos “D” de la masa con respecto a la base; centrándome en ilustrar el proceso didácticamente tomando como referencia tres valores de periodo natural “Tn” (representativo de tres casos de estructuras) y un valor de “ξ” en el orden de “5%”, dado que uno de los propósitos que se buscaba era demostrar la utilidad de expresiones sencillas, que permiten transformar los desplazamientos “D” a valores de pseudo-velocidad “V” y pseudo-aceleración “A”.
Siguiendo la misma metodología, en este artículo construiremos el espectro de respuesta elástico con un amplio rango de valores de período natural “Tn” y para distintos valores de fracción de amortiguamiento crítico “ξ”, lo cual es necesario para establecer las zonas espectrales, que nos dan nociones para saber ante cuál de los parámetros de la fuente sísmica (aceleración “üg(t)”, velocidad “ůg(t)”, desplazamiento ug(t)), la estructura que se analiza presenta mayor sensibilidad, dedicando especial atención a la influencia de los valores de “ξ”, trabajando así con distintos casos que abarcan el rango de valores de “ξ=0%”, “ξ=1%”, “ξ=5%”, “ξ=10%” y “ξ=20%”, con la intención de que potencies querido lector, un pensamiento crítico acerca de esta propiedad dinámica, lo cual es un aporte de mucho interés que viene a complementar las ideas disertadas en la referencia N°06, donde la carga externa estaba representada por una fuerza armónica.
Imagen N°01: una visión global de los contenidos a estudiar
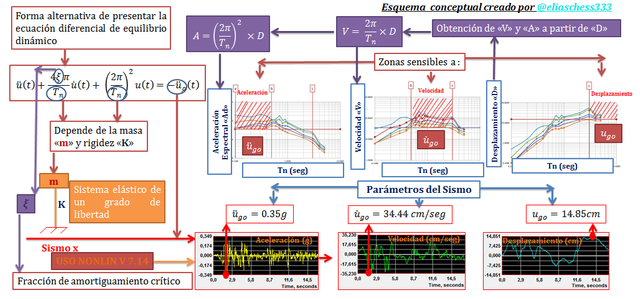
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. Los gráficos que describen los parámetros del sismo provienen de la herramienta computacional NONLIN V 7.14. Los gráficos de los espectros se realizaron con la herramienta Microsoft Excel, con data proveniente del programa NONLIN V 7.14.
Recomiendo la revisión de la referencia N°04 y N°05, donde podrás profundizar en las nociones fundamentales del período natural “Tn” y la fracción de amortiguamiento crítico “ξ”, lo cual es esencial para adentrarnos en tópicos de mayor complejidad en el campo de la ingeniería sismoresistente, como lo es el tema que nos ocupa.
DELIMITACIÓN DE LA TEMÁTICA A ESTUDIAR
En esta oportunidad he optado por presentar la delimitación de la temática a través de un recurso audio-visual, disfruten del siguiente video:
Fuente: @eliaschess333, año: 2018. Nota: video elaborado por el autor con ayuda de las herramientas computacionales Camtasia Studio 8, Adobe Audition 3.0. Las capturas de video fueron realizadas con mi dispositivo Tablet VIT-T4000, y las mismas estuvieron a cargo de @monserratt3. Los esquemas conceptuales que se presentan fueron elaborados por el autor con las herramientas Microsoft PowerPoint y Paint.
RELACIÓN DE LOS PARÁMETROS DE LA EXCITACIÓN SÍSMICA CON LA RESPUESTA DE LA ESTRUCTURA Y LA DEFINICIÓN DE LAS ZONAS ESPECTRALES
La aceleración que experimenta el terreno “üg(t)” ante la ocurrencia de un sismo, es una forma cuantitativa de describir la intensidad de estos fenómenos, y es un parámetro de gran importancia en el análisis y diseño sismoresistente de las estructuras; no obstante, dependiendo de las propiedades de masa “m” y rigidez “K” de estas, se puede obtener un amplio rango de valores de períodos naturales “Tn” que pueden hacer que la estructura sea sensible a otros parámetros de la excitación sísmica, tales como la velocidad del terreno “ůg(t)” y el desplazamiento “ug(t)” de este.
Por ejemplo, en el recurso audiovisual se demostró a través de un “experimento casero” que estructuras muy flexibles, con un “Tn” que tiende teóricamente al “infinito”, la respuesta estructural está marcada por el desplazamiento que experimenta el terreno “ug(t)”. Por su parte, para el caso de estructuras muy rígidas con un “Tn” que teóricamente tiende a “cero”, la respuesta estructural está controlada por la aceleración del terreno “üg(t)”. Adicionalmente existe un rango intermedio de períodos naturales “Tn”, donde la respuesta de la estructura puede estar controlada por la velocidad del terreno “ůg(t)”. Todas estas ideas sugieren la importancia del desarrollo de espectros de respuestas, en los cuales podemos apreciar gráficamente la interacción de “Tn” con un determinado valor de respuesta máxima de la estructura, respuesta que puede ser en términos de aceleraciones espectrales “Ad” totales, pseudo-velocidades “V” y desplazamientos “D” relativos de la masa con respecto a la base (ver imágenes N°03,N°04 y N°05).
En lo que respecta a la relación de los parámetros de la excitación sísmica con las zonas del espectro de respuesta, las siguientes interrogantes permiten orientar las ideas al respecto:
¿Es necesario tomar como referencia en el establecimiento de las zonas espectrales algún dato del acelerograma?
Siendo la respuesta afirmativa, y refiriéndose este dato específicamente a la aceleración máxima del terreno “üg(o)” expresada típicamente como una función de la gravedad, la cual para el caso en estudio es “0.35g” y al momento de ser usado como frontera inferior de los valores de aceleración espectral “Ad” es necesario dividirla por “g”, dado que las aceleraciones espectrales son adimensionales. Se tiene por lo tanto que aquellas zonas del espectro, que caen por debajo de “Adg(o)=0.35”, no se consideran zonas sensibles a la aceleración del terreno, tal como se aprecia en la imagen N°01, y que en la imagen N°02 se ilustra de forma más ampliada, a modo de una función constante “línea de color rojo” que divide en dos partes el espectro de pseudo-aceleración.
¿Y qué hay de los valores de referencia a usar para el caso de las zonas del espectro de respuesta sensibles a la velocidad “ůg(t)” y desplazamiento “ug(t)” del terreno?
Aquí entra la importancia de conocer no sólo el acelerograma (registro de la aceleración del terreno en el tiempo), sino también los registros de velocidad “ůg(t)” y desplazamiento “ug(t)”del terreno en el tiempo; obteniéndose estos últimos por medio de procesos matemáticos de integración, utilizando en este trabajo la herramienta computacional NONLIN V 7.14 para tal fin. Los valores de referencia a los que se le hace alusión en el planteamiento de la interrogante están representados por la velocidad máxima “ůg(o)” y el desplazamiento máximo del terreno “ug(o)”; ilustrados en la imagen N°02 a modo de una función constante, representada por las líneas de color “azul” y “verde” respectivamente, dividiendo el espectro de pseudo-velocidad y desplazamiento en dos partes. Aquellas zonas del espectro de respuesta que caen por debajo de estos valores no son sensibles a los parámetros sísmicos de velocidad “ůg(t)” y desplazamiento “ug(t)” del terreno (ver imagen N°01).
Imagen N°02: excitación del terreno producto del sismo “El Centro, California (1940)” en términos de aceleración, velocidad y desplazamiento
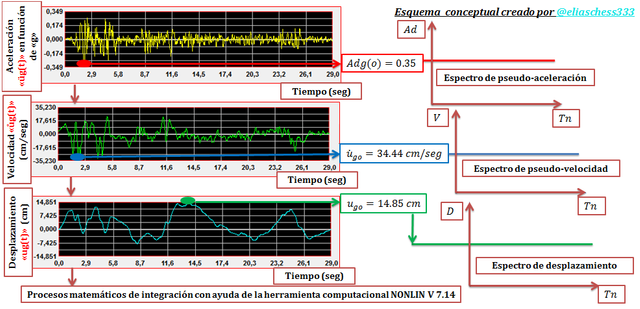
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. Los gráficos que describen los parámetros del sismo provienen de la herramienta computacional NONLIN V 7.14.
NOCIONES GENERALES PARA LA CONSTRUCCIÓN DEL ESPECTRO DE RESPUESTA
En la referencia N°03 puedes disfrutar de los procedimientos de rutina que con ayuda de la herramienta computacional NONLIN V 7.14 permiten obtener valores de desplazamientos relativos máximos de la masa con respecto a la base “D” para un determinado valor de “Tn”, así como el uso de las expresiones que se reseñan en la imagen N°01, que permiten obtener los valores de pseudo-velocidad “V” relativa de la masa con respecto a la base y aceleración espectral “Ad” total. Vale destacar que el espectro de aceleración espectral, refleja valores totales, es decir, para un determinado valor de período natural “Tn”, el valor de “Ad” que se obtiene involucra la respuesta del terreno así como el movimiento relativo de la masa con respecto a la base; resultando que para el caso hipotético de un sistema estructural con “Tn=0seg” el “Ad” se asocia únicamente al terreno, ya que para estos valores de periodo natural, la masa no experimenta movimiento relativo con respecto a su base, tal como se demostró en el “experimento casero” presentado en el recurso audiovisual.
INTERPRETACIÓN CUALITATIVA DE LA ECUACIÓN DIFERENCIAL DE EQUILIBRIO DINÁMICO Y SU ASOCIACIÓN CON LAS ZONAS ESPECTRALES
Surge la cuestión para los fines de este trabajo, de afianzar nuestro sentido crítico acerca de cada uno de los componentes de la ecuación diferencial de equilibrio dinámico, que es resuelta por los procedimientos de rutina comentados en líneas anteriores, y sobre los que puedes profundizar en la referencia N°03. La ecuación en cuestión es:
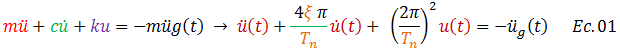
Un análisis cualitativo de esta ecuación permite afianzar la idea de que la respuesta estructural está condicionada a las propiedades de inercia, de amortiguamiento y de rigidez de la estructura (términos resaltados en colores rojo, verde y púrpura), las cuales se pueden representar de forma alternativa con los términos resaltados en color “naranja” como lo son el período natural “Tn” y la fracción de amortiguamiento crítico “ξ”, constituyendo uno de los aportes del presente trabajo, el de analizar como los valores de “ξ” juegan un rol importante en las distintas zonas espectrales. Una interrogante que se viene a la mente cuanto estudiamos estos temas es la siguiente:
¿Se asocian las zonas espectrales con los términos de la ecuación diferencial de equilibrio dinámico?
De acuerdo a lo expuesto en líneas anteriores, las zonas espectrales marcan la sensibilidad de la respuesta de la estructura hacia la aceleración “üg(t)” , velocidad “ůg(t)” y desplazamiento “ug(t)” del terreno; variables resaltadas por el color “magenta” en la ecuación N°01 contextualizadas al movimiento de la masa con respecto a la base; de lo que se puede deducir que el aporte de cada una de estas variables a la respuesta, estará condicionado a la zona del espectro en la que se ubique el periodo natural de la estructura en estudio, con los respectivos valores de fracción de amortiguamiento crítico que se esté trabajando. En los tópicos que siguen, se afianzan de mejor manera las ideas disertadas hasta el momento, resaltando que la data para la construcción de los espectros proviene de la herramienta computacional NONLIN V 7.14, y fue procesada con la herramienta Microsoft Excel.
ESTUDIO DE LA ZONA SENSIBLE A DESPLAZAMIENTO EN BASE A LAS PROPIEDADES DINÁMICAS DE “Tn” Y “ξ”
Tomemos como base de estudio el esquema conceptual que se presenta en la imagen N°03:
Imagen N°03: espectro de respuesta de desplazamiento, para distintos valores de “ξ”
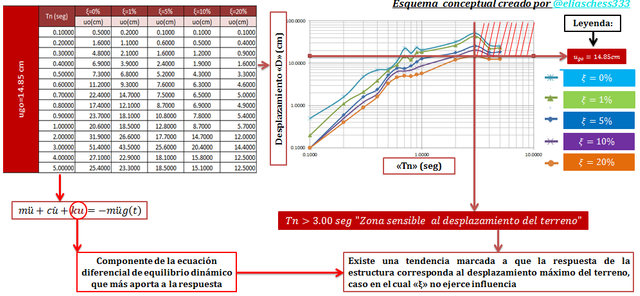
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El gráfico del espectro se realizó con la herramienta Microsoft Excel, con data proveniente del programa NONLIN V 7.14.
Según Chopra (2014):
En una porción de períodos naturales “Tn” comprendida en el rango de "3seg" a "10seg" el desplazamiento relativo de la masa con respecto a la base “D” puede idealizarse como una constante con un valor igual a “ugo” amplificada por un factor que depende de “ξ”.
De acuerdo a la data obtenida gracias a la solución de la ecuación diferencial de equilibrio dinámico para distintos valores de periodo natural “Tn”, es claramente observable en el espectro de desplazamiento, que hay una tendencia marcada al hecho de que mientras mayor sea el valor de “Tn” la respuesta de la estructura es aproximadamente igual al desplazamiento máximo del terreno “ug(o)”, esto debido, a que la estructura es cada vez más flexible, ocurriendo en casos extremos que la masa permanece inmóvil, desplazándose únicamente el terreno; lo cual fue ilustrado en el recurso audiovisual.
Atendiendo a lo que señala Chopra (2014), se aprecia claramente como el caso de las estructuras con una fracción de amortiguamiento crítico de “ξ=0%” experimenta los máximos desplazamientos, los cuales disminuyen en la medida que “ξ” aumenta; obteniéndose inclusive para el caso de “ξ=20%” desplazamientos de la masa con respecto a la base, por debajo del máximo del terreno “ug(o)”; no obstante en la medida que la estructura se haga más flexible, la respuesta tenderá a este último valor, resultando despreciable la influencia de “ξ”. Te invito a que revises la referencia N°05, para que profundices en la comprensión “ξ”.
ESTUDIO DE LA ZONA SENSIBLE A VELOCIDAD EN BASE A LAS PROPIEDADES DINÁMICAS DE “Tn” Y “ξ”
Basados en el esquema conceptual de la imagen N°04 tenemos lo siguiente:
Imagen N°04: espectro de respuesta de pseudo-velocidad para distintos valores de “ξ”
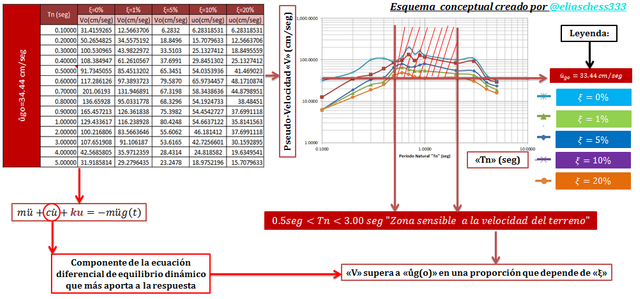
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El gráfico del espectro se realizó con la herramienta Microsoft Excel, con data proveniente del programa NONLIN V 7.14.
Según Chopra(2014):
Para los sistemas estructurales con un período intermedio entre “0.5 seg” y “3 seg”, se tiene que “V” es mayor a “ůgo”. En este intervalo “V” puede idealizarse como una constante con un valor igual a “ůgo” amplificado por un factor que depende de “ξ”.
Es interesante como las nociones teóricas señaladas en el párrafo anterior se adaptan a lo observado en los modelos experimentales desarrollados con ayuda de la herramienta computacional NONLIN V 7.14, lo cual está demarcado por las líneas de color “rojo” que se ven en el gráfico de la imagen N°04.
Esta zona resaltada por las líneas de color “rojo” se conoce como zona sensible a la velocidad, porque la respuesta estructural está condicionada a la velocidad máxima del terreno como frontera mínima de magnitud. Observándose los valores máximos de pseudo-velocidad para los valores más pequeños de “ξ”.
En este tipo de espectros, surge una cuestión importante que debe ser señalada, y es la referida a la extensión de esta franja sensible a la velocidad, que adicional a las propiedades dinámicas de la estructura en cuestión, está sujeta a propiedades adicionales de la fuente sísmica, entre las que destaca la distancia desde donde se hizo el registro del acelerograma a la fuente de la falla, sobre este aspecto estaré profundizando en la parte II de este entrega, y que al mismo tiempo abre las puertas a otros temas de importancia en la ingeniería sismoresistente, como lo son los modelos de atenuación.
ESTUDIO DE LA ZONA SENSIBLE A ACELERACIÓN EN BASE A LAS PROPIEDADES DINÁMICAS DE “Tn” Y “ξ”
Tomando como referencia el esquema conceptual de la imagen N°05, se desprenden las siguientes ideas:
Imagen N°05: espectro de respuesta de pseudo-aceleración para distintos valores de “ξ”
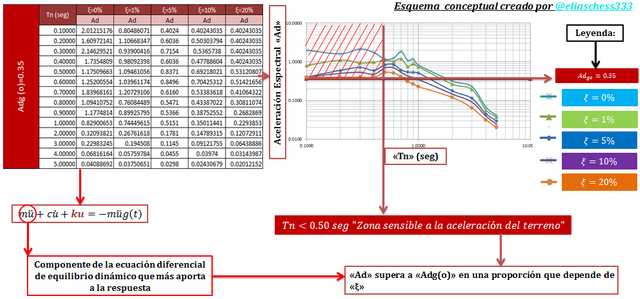
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El gráfico del espectro se realizó con la herramienta Microsoft Excel, con data proveniente del programa NONLIN V 7.14.
Para el caso de las estructuras con “Tn” bajos, menor a “0.50 seg”, la respuesta está notoriamente influenciada por la aceleración del terreno “üg(t)”, disminuyendo sus valores de manera inversa proporcional a la fracción de amortiguamiento crítico “ξ” . Es importante recalcar que el espectro de pseudo-aceleración, cuando es evaluado para un “Tn=0seg” permite obtener la aceleración espectral máxima del terreno “Adg(o)”. Notemos que en esta zona sensible a la aceleración del terreno, lo valores de respuesta de la estructura superan el valor de “Adg(o)” representado a modo de función constante por la línea horizontal que atraviesa el espectro.
En cada una de las zonas del espectro de respuesta, es muy notoria la influencia de la fracción de amortiguamiento crítico “ξ” en cuanto a las magnitudes de respuesta, lo cual al mismo tiempo está vinculado a las propiedades intrínsecas del sistema estructural que se analiza, representadas por el periodo natural “Tn”. En el tópico que sigue, se presenta una forma alternativa de ver tal influencia.
UNA FORMA ALTERNATIVA DE VER LA INFLUENCIA DE LA FRACCIÓN DE AMORTIGUAMIENTO CRÍTICO “ξ” EN LA RESPUESTA ESTRUCTURAL EN TÉRMINOS DE ACELERACIÓN ESPECTRAL “Ad”
Este tópico surge para satisfacer la curiosidad sobre la incidencia que tiene el aumentar el valor de “ξ” basados en un valor previamente establecido en la respuesta estructural en términos de aceleración espectral, que para este fin se normaliza con la obtenida para un “ξ=0%”. En sí, lo que se quiere demostrar busca dar respuesta a la siguiente interrogante:
¿Será lo mismo la influencia que tiene en la respuesta estructural pasar de un valor de “ξ=1%” a un valor de ξ=5%”, que cuando se pasa de un valor de “ξ=10%” a un valor de ξ=15%”?
Siendo por lo tanto necesario la construcción de un gráfico donde en las abscisas se encuentren los valores de fracción de amortiguamiento crítico “ξ” y en las ordenadas las aceleraciones espectrales para un valor dado de “ξ”, normalizadas con respecto a la aceleración espectral para un “ξ=0%”. Dentro de este gráfico pueden existir distintas curvas para cada “Tn” representativos de un determinado sistema estructural, seleccionando en este artículo los periodos naturales en el orden de: “0.20 seg”, “0.50 seg”, “1.00 seg”, “3.00 seg” y “5.00 seg”. A continuación se presenta un cálculo tipo, como ejemplo para el caso de “Tn=0.20 seg”.
Para un “Tn=0.20 seg”, al revisar la tabla del esquema conceptual de la imagen N°05 para “ξ=0%” corresponde un “Ad” aproximadamente de “1.6097”. Este valor divide a las aceleraciones espectrales asociadas a este valor de período natural, para los distintos casos de fracción de amortiguamiento crítico, obteniendo lo siguiente:
Caso 1, ξ=0%
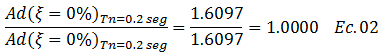
Caso 2, ξ=1%
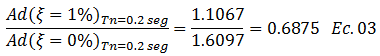
Caso 3, ξ=5%
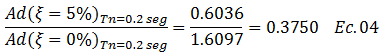
Caso 4, ξ=10%
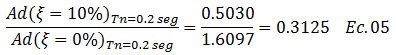
Caso 5, ξ=20%
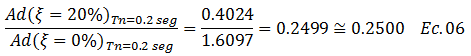
En la imagen N°06 se presenta una data con su respectivo gráfico que involucra distintos valores de “Tn”:
Imagen N°06: estudio de la variación espectral para distintos valores de “ξ”
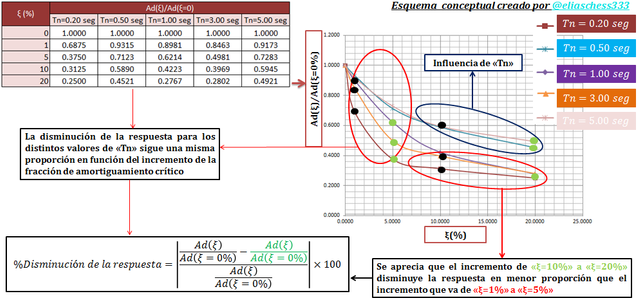
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El gráfico del espectro se realizó con la herramienta Microsoft Excel, con data proveniente del programa NONLIN V 7.14.
Con la ecuación presentada en la imagen anterior, procederemos a cuantificar las observaciones cualitativas allí realizadas, tomando como referencia los puntos de color “negro” y “verde” que se encuentran en el gráfico. En este orden de ideas se tiene lo siguiente:
Caso 1: el amortiguamiento varía de ξ=1% a ξ=5%
• Caso 1.1, Tn=0.20 seg
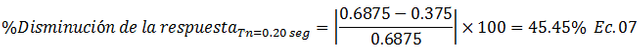
• Caso 1.2, Tn=0.50 seg
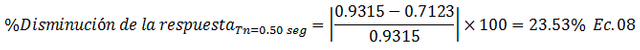
• Caso 1.3, Tn=1.00 seg
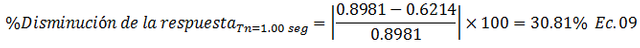
• Caso 1.4, Tn=3.00 seg
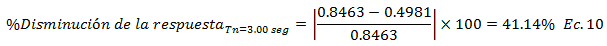
• Caso 1.5, Tn=5.00 seg
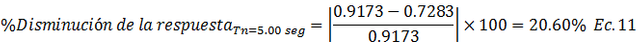
Caso 2: el amortiguamiento varía de ξ=10% a ξ=20%
• Caso 2.1, Tn=0.20 seg
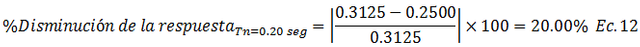
• Caso 2.2, Tn=0.50 seg
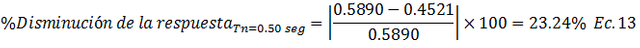
• Caso 2.3, Tn=1.00 seg
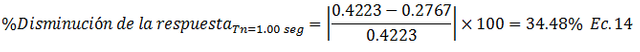
• Caso 2.4, Tn=3.00 seg
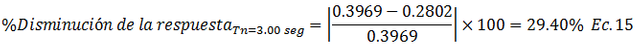
• Caso 2.5, Tn=5.00 seg
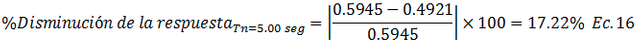
Organizamos los resultados obtenidos en la siguiente tabla:
Tabla N°01: contraste de resultados

Fuente: @eliaschess333. Año: 2018
Al comparar los resultados de disminución de la respuesta para los casos de estudio N°01 y N°02, la apreciación cualitativa hecha en el esquema conceptual de la imagen N°06 aplica a la mayoría de los casos de valores de “Tn” a excepción del valor de “Tn=1.00 seg”. Estos resultados permiten dar respuesta a la interrogante planteada al inicio de este tópico, concluyendo que sí existe una diferencia notable en el porcentaje de disminución de la respuesta, cuando la variación del valor de la fracción de amortiguamiento crítico “ξ” parte de un valor mínimo (caso 1) que cuando la variación parte de un valor “ξ alto” (caso 2).
Centrando la atención en los resultados obtenidos para el caso de “Tn=1.00 seg”, podemos respaldarnos en la siguiente aseveración según Chopra (2014):
El efecto del amortiguamiento en la reducción de la respuesta depende del período natural
Una aseveración que sugiere que el comportamiento de las estructuras ante una excitación sísmica no está marcado por una tendencia monótona, muestra de ello está en la sinopsis de resultados presentada en la tabla N°01, donde la diferencia porcentual del caso 2 es mayor a la del caso 1, contrario a lo que pasó para los demás valores de “Tn”, a pesar de que todos los sistemas estructurales están sujetos a la misma excitación del terreno, correspondiente al sismo “El Centro, California, 1940”.
CONCLUSIONES
Es importante en nuestra formación como ingenieros sismoresistentes comprender la influencia de las propiedades dinámicas de sistemas estructurales sencillos en su respuesta ante una determinada excitación, y así ir desarrollando sólidas bases que permitirán adentrarnos en aplicaciones de mayor complejidad. Entre las conclusiones de mayor importancia de este trabajo, tenemos las siguientes:
1.-La zona espectral sensible a la velocidad puede verse reducida en cuanto al rango de valores de períodos naturales, dependiendo de la distancia de donde se registró el acelerograma con relación a la fuente del sismo. Sobre este aspecto estaré profundizando en la parte II de este post.
2.-Los sistemas estructurales que carecen de rigidez, es decir, períodos naturales muy altos, tienen la característica de que su respuesta estructural ante la excitación sísmica, está condicionada a los parámetros de desplazamiento del terreno.
3.-La zona sensible al parámetro de aceleración del terreno en el espectro de respuesta, está representada por los sistemas estructurales de mayor rigidez, es decir, valores bajos de períodos naturales, típicamente menor a “0.5 segundos”.
4.-La fracción de amortiguamiento crítico “ξ” juega un papel muy importante en la disminución de la respuesta estructural, para las zonas espectrales sensibles a la aceleración y velocidad del terreno.
5.- En el caso de la zona sensible al desplazamiento del terreno, y especialmente en el caso de valores de períodos naturales muy altos, la influencia de “ξ” es depreciable, puesto que la respuesta estructural estará condicionada a “ug(o)”.
Espero este post haya sido de su agrado. Nos leemos en una próxima oportunidad.
FUENTES DE INFORMACIÓN CONSULTADAS
01.- CHOPRA ANIL K. 2014. DINÁMICA DE ESTRUCTURAS. CUARTA EDICIÓN. PEARSON EDUCACIÓN, MÉXICO.
02.- NONLIN “EDUCATIONAL PROGRAM FOR LEARNING THE CONCEPTS OF STRUCTURAL DYNAMICS AND EARTHQUAKE ENGINEERING”. DEVELOPED BY DR. FINLEY CHARNEY, NONLIN IS AVAILABLE AS ONLINE TOOL THROUGH NEESHUB: HTTP://NEES.ORG/
LECTURAS RECOMENDADAS
03.- SANTANA E. 2018. APRENDIENDO A CONSTRUIR UN ESPECTRO DE RESPUESTA ELÁSTICO A PARTIR DE LA EXCITACIÓN SÍSMICA DE SISTEMAS DE UN GRADO DE LIBERTAD. APLICACIONES EN LA INGENIERÍA SISMORESISTENTE. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/aprendiendo-a-construir-un-espectro-de-respuesta-elastico-a-partir-de-la-excitacion-sismica-de-sistemas-de-un-grado-de-libertad
04.- SANTANA E. 2018. COMPRENDIENDO LAS APLICACIONES DE LAS MATEMÁTICAS EN LA ESTIMACIÓN DEL PERIODO Y FRECUENCIA NATURAL DE UN PÓRTICO PLANO. CASO: SISTEMA DE UN GRADO DE LIBERTAD. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/comprendiendo-las-aplicaciones-de-las-matematicas-en-la-estimacion-del-periodo-y-frecuencia-natural-de-un-portico-plano-caso
05.- SANTANA E. 2018. DETERMINACIÓN EXPERIMENTAL DEL AMORTIGUAMIENTO EN ESTRUCTURAS. UN ENFOQUE MATEMÁTICO CON APLICACIONES EN LA INGENIERÍA SISMORESISTENTE. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/determinacion-experimental-del-amortiguamiento-en-estructuras-un-enfoque-matematico-con-aplicaciones-en-la-ingenieria
06.- SANTANA E. 2018. ESTUDIO DE LA SENSIBILIDAD DE LA RESPUESTA DE UNA ESTRUCTURA PARA DISTINTOS CASOS DE FRACCIÓN DE AMORTIGUAMIENTO CRÍTICO “ξ” EN BASE A LA DURACIÓN DE LA EXCITACIÓN EXTERNA. APLICACIONES EN LA INGENIERÍA SISMORESISTENTE.DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/estudio-de-la-sensibilidad-de-la-respuesta-de-una-estructura-para-distintos-casos-de-fraccion-de-amortiguamiento-critico-ks-en
▶️ DTube
▶️ IPFS
Saludos estimado amigo @eliaschess333, muy completo tu artículo, dinámico desde cada uno de los casos presentados, y valioso el enfoque académico de los sistemas estructurales. Felicitaciones.
Estimado @lupafilotaxia, agradecido por tu comentario y apoyo. El estudio de estos sistemas estructurales de un grado de libertad es base fundamental para adentrarnos en aplicaciones de mayor complejidad de la dinámica estructural. Saludos compañero!
Excelente artículo @eliaschess333
Compañero @amestyj agradecido por el apoyo! Saludos!
hola @eliaschess333 es bien tu articulo, lo que me llama la atención es porque hay un desplazamiento alto a los 12,5 s , y las velocidades y aceleraciones no corresponden con ese punto. gracias
Estimado @germanmontero, la pregunta que planteas es muy interesante, y formó parte de mi repertorio de preguntas en mis clases de sismoresistencia. De la revisión de la bibliografía y consulta a profesores, he encontrado como respuesta que este hecho se debe a la distancia de donde se hizo el registro del acelerograma a la fuente sísmica. En los sismos alejados a la falla esto tiende a ocurrir, y cuando son cercanos los registros a la falla, tienden a coincidir en un instante de tiempo los valores máximos. Estas cosas nos revelan lo complejo de la función que rige la excitación del terreno. Representa para mí un reto seguir profundizando en este hecho. Saludos compañero!!
Congratulations @eliaschess333! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
SteemitBoard World Cup Contest - Play-off for third result
Participate in the SteemitBoard World Cup Contest!
Collect World Cup badges and win free SBD
Support the Gold Sponsors of the contest: @good-karma and @lukestokes
@resteemator is a new bot casting votes for its followers. Follow @resteemator and vote this comment to increase your chance to be voted in the future!
Buena información sobre todo por las fuentes de los vídeos esto si es generar contenido..
Gracias @malpica1 por el apoyo. Saludos!