Where does the mass of hadrons come from? (Particle Physics Series – Episode 3B)
Particle physics can be really weird sometimes... An example is that the mass of a composite particule is way larger than that of its constituents.
Compare the mass of a proton with the mass of its quarks: the constituents of the proton only account for about 0.1% of the mass of the whole proton. What’s going on here? Where do the other 99.9% come from?
In this episode we will realize that most of the mass of the proton comes from the energy related to the bonds between the quarks. To understand this, in a first section, we will need to explore the relationship between mass and energy.
Then, we will learn how to measure the mass of composite particles (hadrons) like protons and mesons. We will realize that there is something really wrong with the results: things just don’t add up.
That will bring us to consider that most of the mass of a hadron comes from the binding of its constituents.You can also consult the video related to this episode (it is less detailed but could be useful as an introduction to this article).
1 / Equivalence mass-energy, what does it mean ?
At school, in physics class, we are taught that during an action, energy is conserved. Similarly, in chemistry, we learn that during a chemical reaction, mass is conserved. Einstein realized in his theory of special relativity that both statements were formerly incorrect: it is the sum of both that is conserved. The reason is that mass is a form of energy: mass can convert into energy and vice versa. His well known formula for a motionless object is
Let’s see how this concept applies at different scales
1.a - Energy conversion at the human scale.
Imagine a spring of stiffness 1000 Newtons per meter. Apply a force on it to compress it by 5 cm and hold it that way. The force required to compress the spring is:
The potential energy stored int he spring will thus be
If we could measure ultra-small mass differences, we would realize that the spring would have gained mass.
Let’s consider another example, involving thermal physics this time. Pour one kilogram of water in a container and heat it up from 20 to 40 degrees (Celsius). The energy brought to the water is therefore:
This energy adds up to the energy of the water. Here also, the mass of the water increases:
That is still very small, about 1 trillionth of the original mass!
In everyday life, these relative variation are so small they appear completely insignificant. However, when we look at smaller scale physics, where forces involved are huge relatively to the size of the systems, the variations of mass become far from negligible.
1.b - Energy conversion at the atomic scale
Consider an atom of hydrogen. It is composed of a proton as its nucleus and an electron orbiting around it. These two particles stick together because of the attractive electromagnetic force binding them.
We have learned in the
atomic physics series that to separate the electron from its proton, 13,6 eV of energy are required (that is in Joules 2.176 x 10-18J).
This corresponds to a variation of mass of:
This indeed is very small. But wait…
let’s compare it to the mass of a hydrogen atom (1.67 x 10-27 Kg). Now the change of mass is in the order of the millionth of a percent, i.e. many times more significant than with the heated water.
1.c - Energy conversion at the nuclear scale
Let’s dive deeper into the smaller scale of things. Nuclear physics is the science that studies the reactions that occur within and between the nuclei of atoms. Here, the ratio of converted mass into energy becomes significant enough for it to be used on an industrial scale (nuclear power plants).
Let’s consider a reaction of fission of Uranium that can occur in nuclear power plants and measure the mass of the reactants (before the reactions) and the products (after the reaction).
The mass of 1 uranium 238 + 1 neutron is 3.96968 x 10-25 Kg.
The mass 1 Strontium 90, 1 Xenon 146 + 3 neutrons is 3.96672 x 10-25 Kg.
The loss of mass in this reaction is 0.00296 x 10-25 Kg
It may not appear like much, but it does correspond to 0.07% of the original mass (to be compared with the above examples). 1 Kilogram of Uranium going through this fission process would have 0.7 grams of its mass converted into energy. By applying E=mc2, we can calculate that this corresponds to 67 trillion joules!
That’s huge, the equivalent of the energy released by the Hiroshima bomb…
Actually, the fission reaction should be more accurately written as:
Often students ask me: "where does the energy go?". It goes into the kinetic energy of the products of the reaction. We will discuss this in another series of articles dedicated to nuclear physics that I will most probably write in the mid-term future.
1.d - Energy conversion at the particle physics scale
As we have seen, mass to energy conversion becomes more and more significant as we dig deeper into the smallness of reality. At very small scales, the forces involved are unimaginable huge, relatively to the size of the systems considered. For example the strong nuclear force involved in nuclear physics reactions has a magnitude of tens or even hundreds of Newtons, while staying within the tiny confines of a nucleus! For information, tens of Newtons is the magnitude of the force required to lift kilograms of stuff. And that is just at the nucleon level...
Just imagine at the particle physics level what we will be dealing with! We will explore this, but first, let’s look at how we can measure the mass of particles.
2/ Measuring the mass of particles
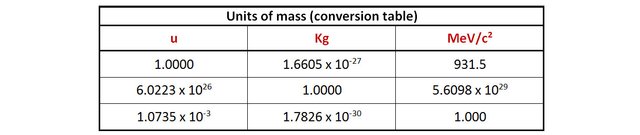
You may have noticed in the previous paragraphs that we are dealing with tiny masses: less than a trillionth of a trillionth of a kilogram. It is necessary to introduce new units of mass to make the data more readable.
An arbitrary unit of mass often used is the unified atomic mass (u). 1 u is equal to 1/12 of the mass of a carbon atom. This leads for example to write the mass of a proton of 1.007276 u, or that of Uranium 238 as 238.050788 u. It is a very practical unit as its value approaches the number of nucleons in a nuclei.
The unit most used in particle physics and nuclear physics, because intuitively linked to energy, is MeV/c2 (It derives directly from E=mc2). For example, an electron (or an anti-electron) has a rest mass of 0.511 MeV/c2, that means that it has a rest energy of 0.511MeV. If it annihilates with its antiparticle, the reaction generates a total of 2 x 0.511 = 1.022 MeV of energy (under the form of 2 photons). Multiply this number by 1,6 x 10-13 to get the energy in Joules.
Measuring the mass of Quarks directly is unfortunately impossible: quarks cannot be observed unbounded, so it is impossible to determine their rest mass. However, the mass of quarks can be predicted within the context of the standard model. In contrast, the mass of composite particles (hadrons) can be directly measured due to how they are affected by a magnetic field. The condition is that these need to be charged.
3/ Measuring the mass of hadrons
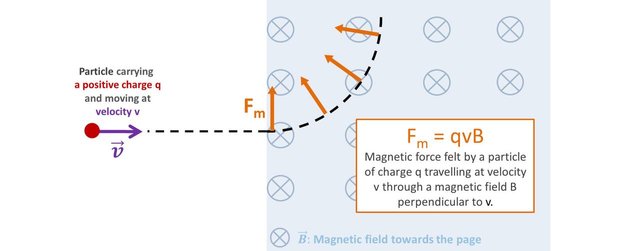
A particle carrying a charge q travelling at a velocity v in a magnetic field B perpendicular to its direction of motion will be subjected to a force of magnitude q x v x B.
Because the magnetic force is always perpendicular to the velocity, the trajectory of the particle follows a circular motion. The magnetic force is said to be centripetal, and is therefore mathematically equal to mv2/r where m is the mass of the particle and r the radius of its circular motion.
This expression can be rearranged to express the mass of the particle as subject:
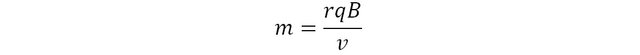
The magnetic field B and the velocity v are set experimentally. the charge is intrinsic to the particle and is known. So one just needs to measure the curvature of its trajectory, and… voila, the experimental mass of the particle can be determined.
Measuring the mass of uncharged particles is also possible but requires using different methods. For the neutron see here. For the neutrino, here is a good starting point.
4/ Comparing the masses of hadrons
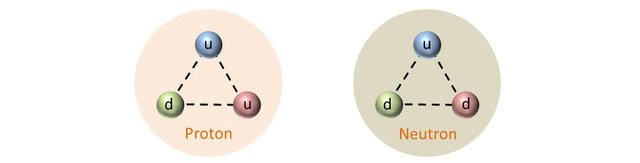
As we have seen previously, protons are composed of two up quarks and one down quark (uud) and neutrons are composed of two down quarks and one up quark (udd). The experimental mass of a proton is about 938 MeV/c2 and that of the neutron is about 940 MeV/c2.
By solving this set of simultaneous equation it is trivial to deduce the mass of the up and down quarks:
OK, let’s check if this way of doing things make sense…
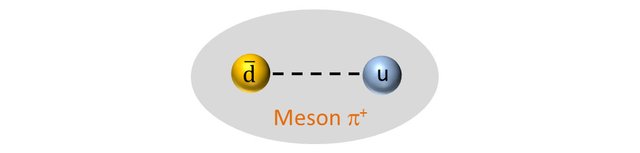
A positive Pion is a meson (a hadron with 2 quarks) composed of an up quark and an anti- down quark (the mass of a quark and its antiquark are identical).
So the positive pion should have a mass of:
If we measure the mass of the positive pion experimentally, the value found is a little less than 140 MeV/c2 ! It doesn’t match! What’s going on here ???
Well, mesons and protons are not the same thing: their respective "quark bonds" must somehow be different, and that reflects on their respective masses…
It appears that the interactions between quarks contribute much more to the mass of the hadron than their intrinsic masses. This is indeed the case as we will see in the next paragraph.
5/ The masses of quarks
It is not possible to measure the intrinsic mass of quarks, but the standard model can predict their value
The mass of the proton is 938 Mev/c2, so this infers that the masses of the quarks that constitute it contribute for about 0.1% of its mass.
Such values are purely theoretical because quarks can never be separated from each other. The strong force that binds them is indeed a weird beast: unlike the gravitational and the electromagnetic forces, it increases dramatically with distance: further you try to take quarks apart from one another, stronger the force between them becomes. This is a characteristic of the strong force called asymptotic freedom.
If you could actually separate them without new quarks being created due to the energy you would bring, you would need to provide an infinite amount of energy to the system and the quarks could then be considered as having an infinite mass… That does not make any sense, so we cannot approach the understanding of the mass of a proton using the traditional Newtonian way.
Instead, we have to consider what’s going on with the particles that mediate the strong force: the gluons…
Let’s start by talking about the photon, the carrier of the electromagnetic force. Like the gluons, these particles of light, are massless. Nonetheless photons do carry energy (E=hf), called photon energy. We wrote earlier that the equivalence between mass and energy is E = mc2. This applies for particles at rest where m here is called the rest mass.
However, if the particle is in motion, Einstein’s well known formula becomes E2=m2c4+p2c2, where the term p2c2 is related to the motion of the particle. One could say that the photon has a “dynamic mass”.
Well, it is a little bit the same thing with the gluons. Their energy is called chromodynamic binding energy. Yet, because gluons cannot be studied individually, this energy is much less well defined than it is with photons.
In addition quarks and gluons in a proton (or any other hadron) are far from being at rest. They are moving around at very large velocities in a beautiful chaos. Their momentum contribute to the total internal energy of the proton.
Seen from outside the confines of the proton, this energy appears as mass, and accounts for nearly 99.9% of the proton's mass
6/ Let's conclude
After realizing that mass and energy are actually the two faces of the same coin, we can understand better the un-intuitive results obtained when determining experimentally the mass of composite particles.
For example, the intrinsic masses of the quarks that form a proton account for only 0.1% of the proton's mass. The other 99.9 % originate from the energy of the gluons that bind the quarks together and the kinetic energy of the quarks themselves.
I find it stunning to see how deeper one explores smallness, the less the concept of mass has meaning in a traditional sense. It appears to fade away...
This is another brick in the affirmation that our reality is really far from being what it seems!
The Video
The 'Particle Physics' series is aimed at providing an introduction to the world of small scale physics to non-scientists and high school students preparing for their high school exams.
Previous episodes:
- Elementary particles, the building block of reality (Particle Physics Series – Episode 1)
- Composite particles: let’s play Lego! (Particle Physics Series – Episode 2)
- Elementary fermions: the particles of matter… (Particle Physics Series – Episode 3A)
Need some more particle physics?
If you wish to sharpen your understanding by approaching particle physics via another angle, please explore @lemouth series of articles on particle physics. You can start here: https://steemit.com/science/@lemouth/the-bestiary-of-particle-physics-this-is-how-i-introduced-particle-physics-to-cern-summer-students
Sources, references and to dig deeper:
- Small Scale Physics Part 1 (booklet written for my students)
- https://en.wikipedia.org/wiki/Neutron#Mass
- https://en.wikipedia.org/wiki/Mass%E2%80%93energy_equivalence#Conservation_of_mass_and_energy
- https://en.wikipedia.org/wiki/Quark
- Physics for the IB diploma (Cambridge Textbook)
- https://en.wikipedia.org/wiki/Gluon
Image credit:
- E = mc2 by Daniele Pellati, public domain [source]
- The decorative picture at the end, the thumbnail background picture and some graphic elements for friezes and illustrations were found on Pixabay.com.
- All illustrations, diagrams and friezes have been produced by me.
- Video and music on video produced by me.
Hi,
I’m @muphy (see intro post),
My life revolves around music production, teaching sciences, and discovery through travel.
You enjoyed that post? Resteem and Upvote!
You are interested in these topics? Follow me!

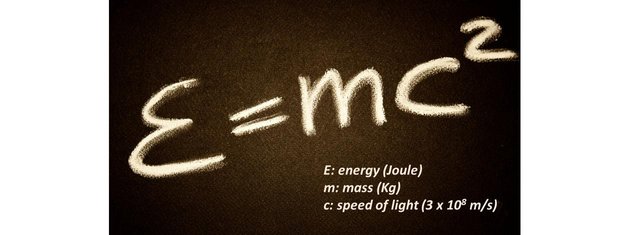
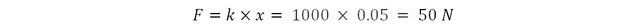
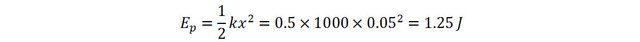
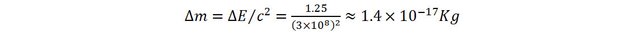

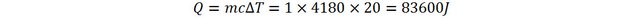
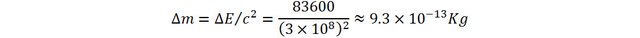


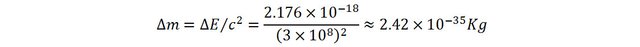

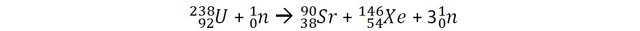


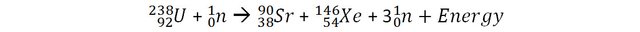


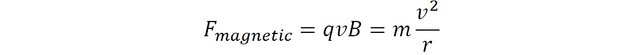
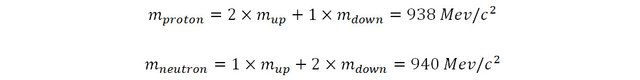

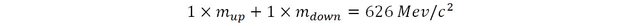




Very nice post! As usual, I have a bunch of comments (you should get used to them by now :p ).
This made me jump out of my chair. Energy conservation is a key principle of physics. Energy is conserved. No matter what. At the fundamental level, energy can however exist under three forms: mass energy, kinetic energy and potential energy. And it is the total energy (the sum of the three) that is conserved.
Along the same line, I am feeling very uncomfortable with your spring example. When you discuss this increase in mass, you actually refer to an increase in relativistic mass. This is very a unpopular concept among particle physicists. The reason is that we name it differently: energy (divided by c2 but for us c=1). The concept of mass is only used for the intrinsic mass of the system. I actually have troubles to understand why people tend to call 'mass' something that is just the total energy of the system.
For the case of the atom, things are slightly different as we are talking about a closed system whose mass is thus defined by its components (their mass and their interaction). This is a different story from the one of your spring.
A detail: except the top quark as it does not hadronize.
PS: I wrote a couple of posts on neutrino physics months ago, if you are interested ;)
good to see this information.. i like it.. hope for another informative blog by you in future...
Amazing post, just followed and resteemed, Follow me back and upvote my posts as well. Hope we can be good friends.
i enjoy your post! thanks
interesting calculation there got to know a lot about it :)
This is a very deep science and a vague philosophy and I read the first time like this good topic and thank you
Great part it was to read and understand the relation between them