Szczególna teoria względności V [Uzupełnienia I]
Chciałbym uzupełnić dotychczasowe rozważania o pewne pomocne wytłumaczenie tych zjawisk na kilku przykładach, które mogą rozjaśnić, chociaż trochę jak wyglądają zjawiska relatywistyczne. Poznamy też kilka paradoksów, które rodzi szczególna teoria względności.
Kontrakcja długości
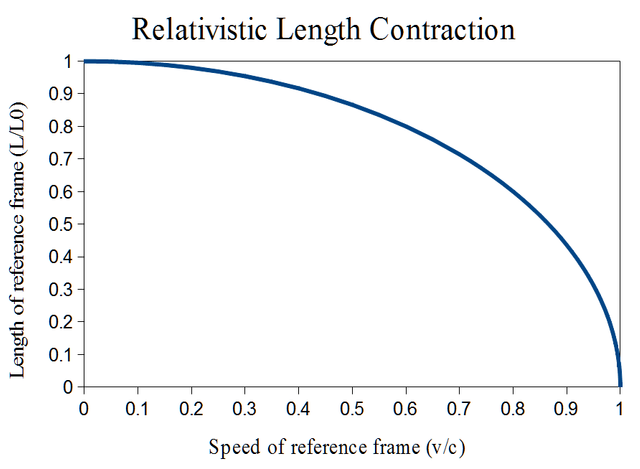
Zacznijmy od analizy wykresu powyżej, przedstawia on zależność pomiędzy długością obiektu, a jego prędkością. W tym przypadku mamy do czynienia z wartościami, które unormowane są do jedynki. Zauważyć można, że dla prędkości nieporównywalnie małych w stosunku do prędkości światła efekt skrócenia jest praktycznie zerowy. Nawet gdy rozpędzimy obiekt do prędkości 0,1c (~30 km/s), nie jesteśmy w stanie zauważyć większych zmian długości obiektu na własne oczy. To dlatego mechanika klasyczna tak dobrze opisuje nasz świat. Zjawiska relatywistyczne zaczynają być widoczne, dopiero przy ogromnych prędkościach, do których nie jesteśmy przyzwyczajeni.
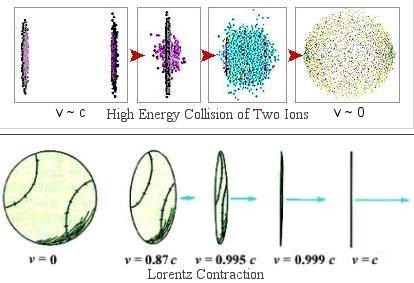
Paradoks tunelu wzdłuż rzeki
Przejdźmy teraz do pewnego paradoksu. Ze skróceniem Lorentza wiąże się oczywiście wiele paradoksów. Okazuje się jednak, że są to sprzeczności pozorne. Wyobraź sobie, że w Twoim mieście wybudowano nowy tunel biegnący wzdłuż rzeki. Patrząc na ten tunel zauważasz wjeżdżającą do niego ciężarówkę. Jest to wyjątkowa ciężarówka z tego powodu, że ma akurat taką długość, że mieści się idealnie na całej długości tunelu. Ciężarówka ta rozpędziła się do tak ogromnych prędkości, że obserwator stojący na zewnątrz stwierdza ze zdziwieniem, że ciężarówka mknąc pod tunelem zajmuje jedynie połowę jego długości (skrócenie Lorentza). Jednakże z punktu widzenia kierowcy to tunel ulega skróceniu i w żadnej chwili ciężarówka nie znajduje się w całości wewnątrz tunelu. Według niego połowa ciężarówki wystaje z tunelu, podczas gdy reszta w całości go wypełnia. Jak to możliwe?
Pozorna sprzeczność wynika z tego, że w problemie tym pojawia się pojęcie jednoczesności (omawiane w jednym z poprzednich artykułów). Mówiąc, że w pewnej chwili ciężarówka znajduje się wewnątrz tunelu stwierdzamy, że jej przednia szyba znajduje się w nim jednocześnie z tyłem ostatniej przyczepy. Oczywiście, chwile, w których zmierzono w tunelu położenie przedniej szyby i ostatniej przyczepy, nie są wcale jednoczesne według kierowcy. Według niego najpierw zostało zmierzone położenie przedniej szyby, a chwilę później, gdy ciężarówka przebyła już jakiś mały odcinek drogi, zmierzone zostało położenie ostatniej przyczepy. Przykład ten uczy ostrożnego przyglądania się wszelkim paradoksom teorii względności. Zawsze powinniśmy zachować czujność na wypadek, czy gdzieś przypadkiem nie pojawia się zdradliwa jednoczesność.
Dylatacja czasu
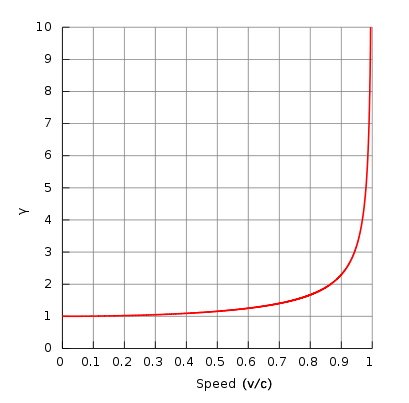
Podobnie sprawa się ma ze zjawiskiem dylatacji czasu. Przy małych prędkościach efekt jest dla nas ludzi niezauważalny. Dopiero przy ogromnych prędkościach możemy zobaczyć różnicę. Jeżeli ktoś porusza się przez 10 lat z prędkością 0,9c (~270000 km/s), to dla obserwatora w spoczynku minie około 23 lata. Gdy będzie poruszał się z prędkością 0,99c (~297000 km/s), to dla obserwatora w spoczynku minie około 71 lat. Gdy prędkość dąży do prędkości światła, to czas, który minie u spoczywającego obserwatora dąży do nieskończoności! Jeżeli policzymy ile lat dla obserwatora stojącego trwa 10-letnia podróż dla obserwatora w pojeździe, który porusza się z prędkością 0,9999c (~299970 km/s!) to złapiemy się za głowę. Trwa około 710 lat. Ale to tak na prawdę nic. Im bliżej c tym dochodzimy do lat liczonych w milionach. Weźmy jeszcze jeden przykład z życia. Stoisz sobie na ulicy i mija Ciebie Twój kumpel w samochodzie z prędkością 100 km/h. Załóżmy, że urodziliście się w tym samym momencie i w tym samym momencie byście umarli. Przeżyjecie 100 lat. Załóżmy teraz, że ten Twój kumpel przez całe swoje życie porusza się z tą prędkością, a Ty przez całe życie stoisz. Okaże się, że jeżeli podstawimy dane do wzoru na dylatację czasu, otrzymamy, że Twój kumpel z Twojego punktu widzenia przeżyje dłużej niż Ty. On natomiast odczuje, że również przeżył 100 lat. O ile dłużej zatem przeżyje? O około 0,0000000005 sekundy. Widzimy więc, że dla naszych codziennych prędkości poprawki wynikające z efektów relatywistycznych są zaniedbywalnie małe. Kolejny przykład, dlaczego mechanika newtonowska jest wystarczająca do opisu naszych codziennych zjawisk mechanicznych.
Źródła obrazków:
Kontrakcja I
Kontrakcja II
Dylatacja
Spis treści artykułów z serii.
Wprowadzenie
Doświadczenie Michelsona-Morleya
Transformacja czasu
Skrócenie lorentzowskie i równoczesność