Szczególna teoria względności I [Wprowadzenie]

Witam! Jest to pierwszy artykuł z serii o szczególnej teorii względności (STW). Plan jest dosyć prosty. Spróbować wytłumaczyć ją wam w ciekawy i przystępny sposób, aby każdy mógł zapoznać się z teorią, która zmieniła rozumienie czasu i przestrzeni. Przygotowanie fizyczno-matematyczne nie jest raczej wymagane (chociaż czasami mogę nie umieć się opanować). Równania będą pojawiać się opcjonalnie, a wszystko będę starał się tłumaczyć. Zapraszam zatem zainteresowanych.

---

Wprowadzenie

---

Szczególna teoria względności (STW) zaproponowana została przez Alberta Einsteina w 1905 roku. Powstało również jej rozszerzenie znane jako ogólna teoria względności (OTW), która została opublikowana w 1916 roku. Uogólniała ona STW o prawo ciążenia. Nie będziemy się jednak nią tu zajmować.

Pierwszą rzeczą, którą omówimy jest tak zwana zasada względności. Po raz pierwszy została ona zaproponowana przez Isaaca Newtona jako jeden z wniosków wynikających ze sformułowanych przez niego praw ruchu:

"Ruchy ciał zawartych w danym układzie są względem siebie takie same, niezależnie od tego czy układ ten porusza się jednostajnie po linii prostej, czy pozostaje w spoczynku"

Oznacza to, że wszelkie doświadczenia i zjawiska zachodzące w pojeździe, który porusza się ze stałą prędkością po linii prostej, są takie same jak w pojeździe, który nie porusza się w ogóle. Myśl jest dość prosta i jedyne co możemy teraz zrobić, to spytać czy rzeczywiście dla wszystkich doświadczeń przeprowadzonych w poruszającym się pojeździe prawa fizyki okażą się takie same jak w pojeździe, który jest w spoczynku. Sprawdźmy zatem za Newtonem, czy jego prawa okażą się takie same.

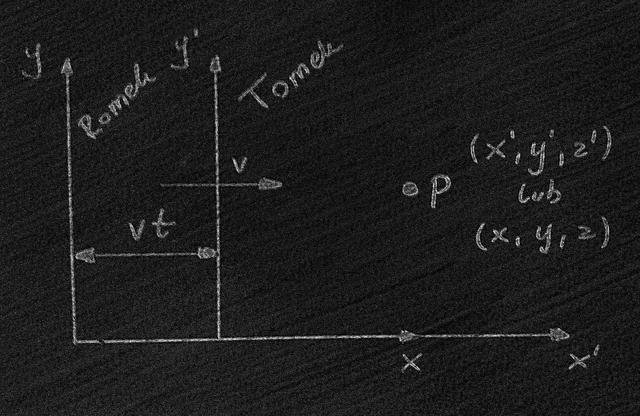
Załóżmy, że Tomek porusza się ze stałą prędkością v w kierunku osi x i że mierzy on położenie pewnego punktu, który pokazany jest na rysunku obok. Odległość "x-ową" tego punktu w swoim układzie współrzędnych oznacza przez x'. Romek natomiast będący w spoczynku mierzy położenie tego samego punktu i oznacza jego współrzędną "x-ową" w swoim układzie współrzędnych jako x. Na podstawie rysunku możemy wnioskować zależność między współrzędnymi Tomka i Romka. Po czasie t początek układu Tomka przesunął się o vt i jeżeli oba układy początkowo (t=0) pokrywały się ze sobą to zależność wygląda jak na rysunku.

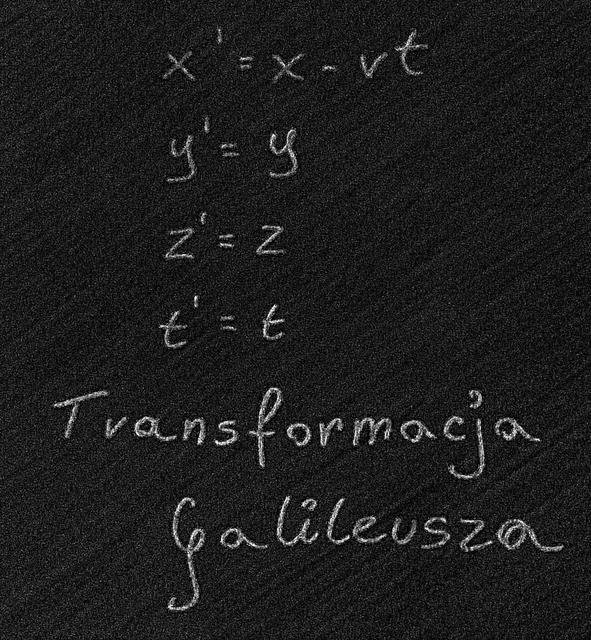
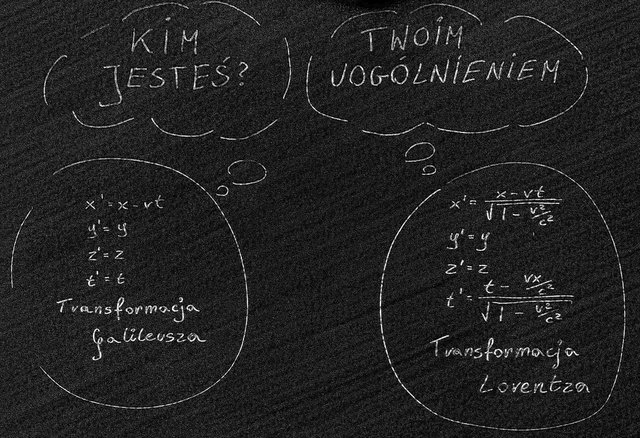
Zależność ta nosi nazwę transformacji Galileusza

Jeżeli zastosujemy to przekształcenie współrzędnych do praw Newtona to okaże się, że otrzymamy te same prawa , lecz w układzie primowanym. Wniosek jest następujący:

Prawa Newtona mają tę samą postać w układzie poruszającym się, jak i w spoczywającym. Nie można więc poprzez dokonywanie doświadczeń mechanicznych stwierdzić, czy układ się porusza, czy też nie porusza.

Zasada względności była stosowana od dawna. Stosował ją między innymi Huygens, dla otrzymania praw opisujących zderzające się kule bilardowe. W XIX wieku z powodu wzmożonych badań związanych z elektrycznością, magnetyzmem i światłem zasada ta zyskała jeszcze bardziej na popularności.

Liczne badania prowadzone przez wielu uczonych znalazły swoje ukoronowanie w sformułowanych przez J.C.Maxwella równaniach pola elektromagnetycznego. Opisują one elektryczność, magnetyzm i światło jako jedną całość. Wydawało się jednak, że równania Maxwella nie spełniają zasady względności. Zauważono, że jeżeli zadziałamy na nich transformacją Galileusza, ich postać nie pozostanie niezmieniona! Wynikało z tego, że zjawiska optyczne i elektryczne zachodzące w poruszającym się pojeździe powinny różnić się od tych samych zjawisk w pojeździe, który spoczywa. Moglibyśmy zatem użyć zjawisk optycznych do wyznaczenia prędkości pojazdu, a w szczególności za pomocą pomiarów optycznych i elektrycznych można byłoby wyznaczyć prędkość bezwzględną pojazdu.
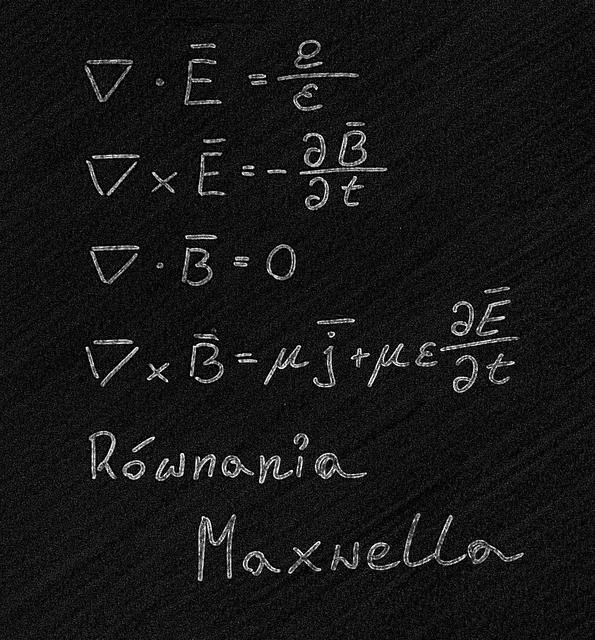
Z maxwellowskich równań wynika między innymi, że gdy mamy do czynienia z zaburzeniem pola, które prowadzi do powstania światła, wytworzone fale elektromagnetyczne rozchodzą się we wszystkich kierunkach równomiernie z szybkością równą c, czyli 300 000 km/s. Wynika z nich również, że gdy źródło zaburzenia porusza się, światło rozchodzi się w przestrzeni z tą samą szybkością c. Podobnie jest ze dźwiękiem, którego fale rozchodzą się niezależnie od ruchu źródła. Prowadzi to do bardzo ciekawego problemu.

Jedziemy samochodem, który porusza się z prędkością v. Samochód nasz zostaje nagle wyprzedzony przez światło biegnące od tyłu z prędkością c. Różniczkując pierwsze z równań transformacji Galileusza otrzymujemy wynik jak na rysunku.

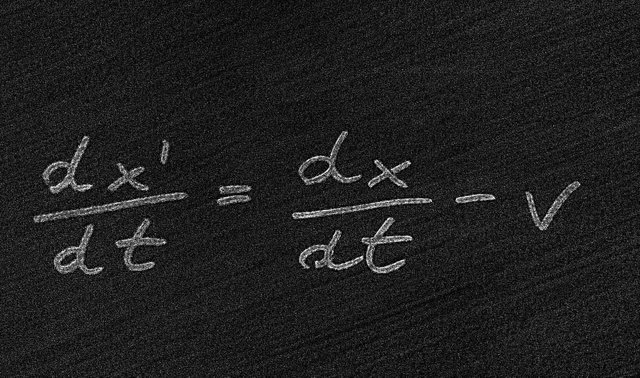
Oznacza to, że według transformacji Galileusza pozorna prędkość światła mierzona w samochodzie nie wyniesie c, lecz c-v. Dla przykładu, jeżeli samochód jedzie z prędkością v=100 000 km/s, to zdawałoby się, że zmierzona w nim prędkość światła wyniesie c=200 000 km/s. Ogólnie można by było zawsze poprzez zmierzenie prędkości światła wyprzedzającego samochód (jeśli transformacja Galileusza jest słuszna dla światła) wyznaczyć prędkość samochodu.

Przeprowadzona została ogromna ilość doświadczeń, w których chciano wyznaczyć prędkość Ziemi, ale wszystkie zakończyły się fiaskiem i nie wykazały żadnej prędkości. Jednym z tych doświadczeń było doświadczenie Michelsona-Morleya, które omówię szczegółowo w kolejnych częściach serii. Coś musiało być przyczyną niepowodzeń. Coś było nie tak z równaniami fizyki. Cóż to mogło być?

---

Przekształcenie Lorentza

---

Gdy fizycy przekonali się, że równania fizyki zawiodły, początkowo przypuszczano, że przyczyna leży w nowych równaniach elektrodynamiki Maxwella (miała wtedy jakieś 20 lat). Wydawało się oczywistym, że równania te muszą być błędne. Starano się zatem tak je przekształcić, aby przy transformacji Galileusza zasada względności pozostawała słuszna. Gdy to zrobiono, okazało się, że nowe człony pojawiające się w równaniach prowadzą do zjawisk elektrycznych, których nie obserwowano doświadczalnie. Podejście to poszło więc do kosza. Równocześnie stawało się coraz to bardziej widoczne, że maxwellowskie prawa elektrodynamiki są prawdziwe i że problem leży gdzie indziej.

Pewnego dnia H.A.Lorentz zaobserwował dziwną rzecz, która godna była uwagi. Gdy dokonał w równaniach Maxwella podstawienia (rysunek), to postać tych równań nie uległa zmianie! Równania te noszą nazwę przekształceń Lorentza (lub transformacji Lorentza). Einstein, idąc za myślą rzuconą pierwszy raz przez Poincarégo, wyraził pogląd, że wszystkie prawa fizyczne powinny mieć tę własność, by pozostawały niezmienione pod wpływem przekształcenia (transformacji) Lorentza. Mówiąc inaczej powinniśmy zmienić nie prawa elektrodynamiki, lecz prawa dynamiki newtonowskiej.

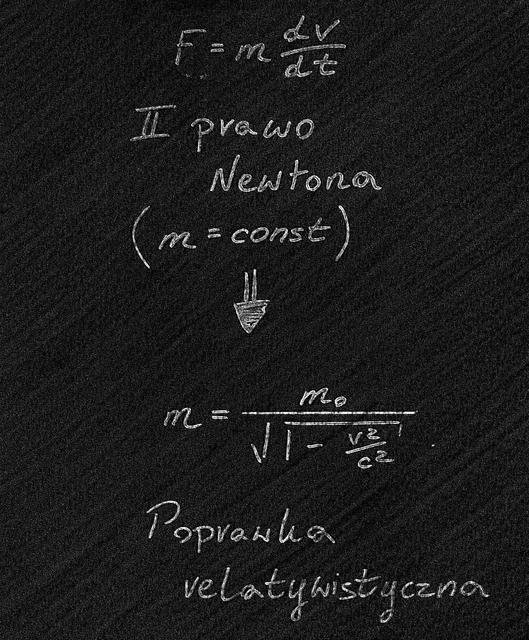
Jak należy zmodyfikować prawa Newtona, aby ich postać nie zmieniała się pod wpływem przekształcenia Lorentza?
Okazuje się, że wystarczy w równaniach Newtona zastąpić masę m nowym wyrażeniem (rysunek). Gdy dokonamy tej zmiany prawa Newtona i prawa elektrodynamiki będą doskonale ze sobą współgrać. Cudowne! Jeżeli użyjemy teraz transformacji Lorentza, dla porównania pomiarów Tomka i Romka, nie uda nam się nigdy wykryć, czy któryś z nich się porusza, gdyż postać wszystkich równań będzie w obu układach współrzędnych taka sama!

Interesującym byłoby rozważenie, co oznacza zastąpienie starego przekształcenia współrzędnych i czasu nowym przekształceniem. Przekształcenie Galileusza wydaje się czymś oczywistym, natomiast przekształcenie Lorentza wygląda dosyć osobliwie. Chcemy zatem wiedzieć, czy możliwe jest zarówno, z punktu widzenia logiki, jak i doświadczenia, że właśnie nowe przekształcenie jest prawdziwe. Aby się o tym przekonać i zrozumieć nową transformację nie wystarczy zająć się jedynie prawami mechaniki, ale podobnie jak to uczynił Einstein, trzeba przeanalizować również pojęcia czasu i przestrzeni. Czeka nas zatem długa droga. Omówienie tych pojęć, jak również płynących z nich konsekwencji dotyczących mechaniki, będzie dość rozległe. Powiem natomiast od razu, że nasz wysiłek okaże się uzasadniony, gdyż otrzymane rezultaty będą zgodne z doświadczeniem.