A Gentle Introduction To Mathematics - Logical Equivalence
In the last post, we've discussed the fact that a conditional and contrapositive have the same logical content. Today, we're going to discuss in depth the idea of "sameness in logical content".
Statements p and q are said to be logically the same or equivalent if they have the same logical content. This is a semantic concept and is useful in the field of computer science, mathematics, and engineering.
Consider the following statements which are logically equivalent[1].
- "If Lisa is in France, then she is in Europe":
In symbols:
- "If Lisa is not in Europe, then she is not in France".
In symbols:
Are we allowed, then to write the following?
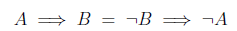
One problem with this is that the equals sign already got a job; it is used to indicate that two numerical quantities are the same. What we are trying to equate here is really sort of different thing!
Nevertheless, there is a concept of “sameness” between certain compound statements, and we need a symbolic way of expressing it.
There are two common notations:
We’ll use the second notation in most of the posts in the coming series. So we can either use
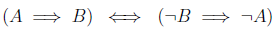
Or
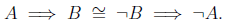
The formal definition of logical equivalence is this:
two compound sentences are logically equivalent if in a truth table that truth values of the two sentences are equal in every row.
As an exercise consider the following truth table, given two compound sentences A and B.
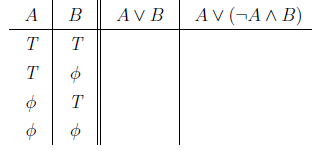
While filling all the logical equivalence of this truth tables might be fun, you will probably eventually come to find it somewhat tedious. A more mature approach to logical equivalence is this: use a set of equivalences – which themselves may be verified via truth tables – as the basic rules or laws of logical equivalence, and develop a strategy for converting one sentence into another using these rules.
This is like doing basic algebra, but the rules one is allowed to use are subtly different.
Commutative Laws
Commutative properties involve spatial or physical order. (Note that there isn’t a commutative law for implication)
Conjunction: denoted by
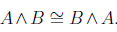
“The weather is cold and snowy” is logically equivalent to “The weather is snowy and cold”. This is apparent in perspective of linguistics. This commutative property is also clear from the perspective of digital logic circuits.
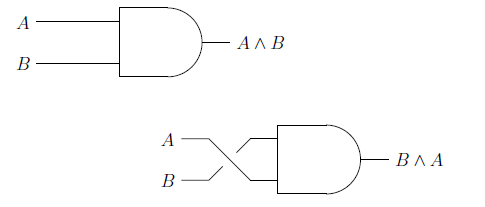
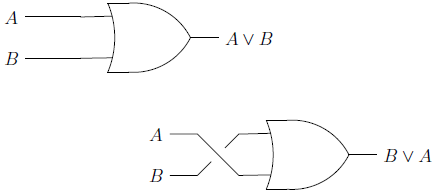
Disjunction: denoted by
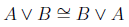
“You either earn more steem dollar or steem” is logically equivalent to “you either earn more steem or steem dollar. The commutative disjunctions are equally transparent from the perspective of a circuit diagram.
Associative Laws
You can think of associative laws as properties that involve temporal order. The associative law of addition in algebra could be used to say we’ll get the same result if we add 2 and 3 first, then add 4, or if we add 2 to the sum of 3 and 4. (i.e. (2+3) + 4 = 2 + (3+4). Note that physically the numbers are in the same order (2 then 3 then 4) but the parentheses indicate precedence in when the plus signs are evaluated.)
Conjunction: denoted by
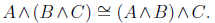
In visual terms, the following two circuit diagrams are equivalent.
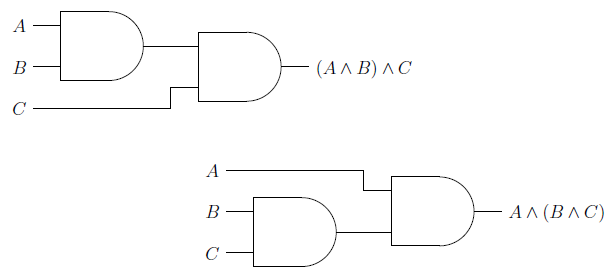
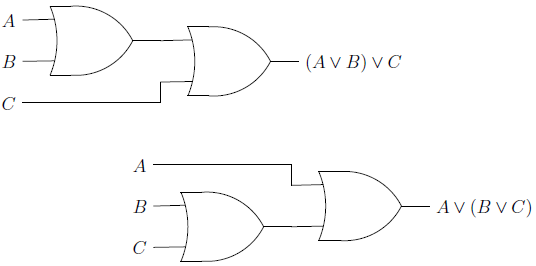
Disjunction: denoted by
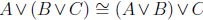
Visually this would look like this,
Distributive Laws
Another example of logical equivalence is the so-called distributive laws. Distributive laws involve the interaction of two operations, when we distribute multiplication over a sum; we effectively replace one instance of an operand and the associated operator, with two instances, as illustrated below,
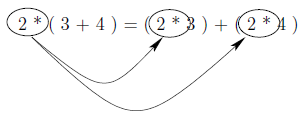
Our case of logical sentences, the conjunction and disjunction operator distributes over the other. Thus we have
Distributive law of conjunction over disjunction
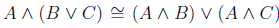
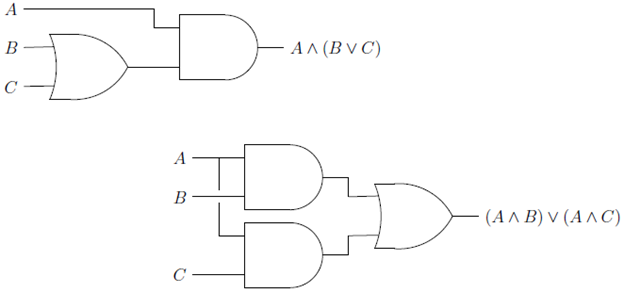
Visually expressed in circuit diagram as,
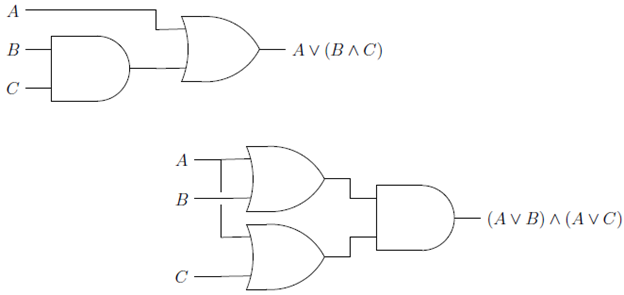
Distributive law of disjunction over conjunction
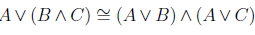
And the circuit diagram is expressed as,
Distributive law of negation
In basic algebra, the distribution of the minus sign over a sum is easy to figure out,
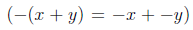
What is the corresponding distribution of negation in Boolean algebra? At first blush, one might assume the analogous thing would be something like,
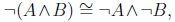
But we can easily dismiss this just by looking at the corresponding truth table,

The secret to the distribution of negation in Boolean algebra turns out to be a set of rules known as DeMorgran’s law, which basically say that you can distribute the negative sign but you must also change the operator.
The DeMorgan’s law are the following:
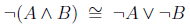
and
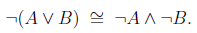
Inverse
In ordinary arithmetic there are two notions of “inverse”, the negative of a number known as the additive inverse and the reciprocal of a number known as its multiplicative inverse.
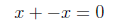 | |
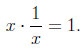 |
In Boolean algebra, there is only one “inverse” concept, the denial of a predicate (i.e. logical negation), but the equations above have analogous, as do the symbols 0 and 1 that appear in them.
Consider the row in the table below, that is the logical or of a statement and its exact opposite; when one is true the other is false and vice versa. But this kind of disjunction is always true! To be or not to be. We use the symbol t, it stands for tautology, to represent a compound sentence whose truth value is always true. Similar kind of thinking leads us to the definition of c, which stands for contradiction to represent a sentence that is always false. To be and not to be., it's contradicting!!
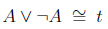 | |
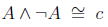 |
The rules above, which we have been discussing, are known as complementarity laws.
Identity Laws
Now that we have the special logical sentences represented by t and c we can now discuss identity laws.
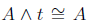 | |
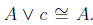 |
Performing a tautology on a conjunction is sort of like multiplying by 1. On the contrary, performing a disjunction with a contradiction also has no effect, akin to adding 0.
Domination property
In basic algebra, the number zero has a special property:
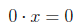
An equation that holds true no matter what x is. This is the domination property. Note that there isn’t a dominance rule for 1. However, in Boolean algebra both the symbol t and c have related domination rules.
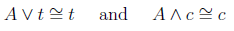
Idempotent
In mathematics, the word idempotent is used to describe situations where a power of a thing may be equal to that thing. In algebra, the third power of negative one is still a negative one, we say that -1 is idempotent. In Boolean algebra, both of the logical operators have idempotence relations that always work. In algebra, its difficult to find idempotents, but in Boolean algebra, every statement is equivalent to its square – where the square of A can be interpreted as either 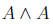 or
or 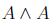 .
.
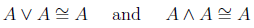
Absorption
We should also mention this strange property called absorption, which states that the expressions
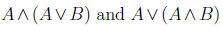
don't actually have anything to do with B at all! (B is totally absorbed by the presence of double A). Both of the preceding statements are equivalent to A.
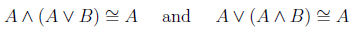
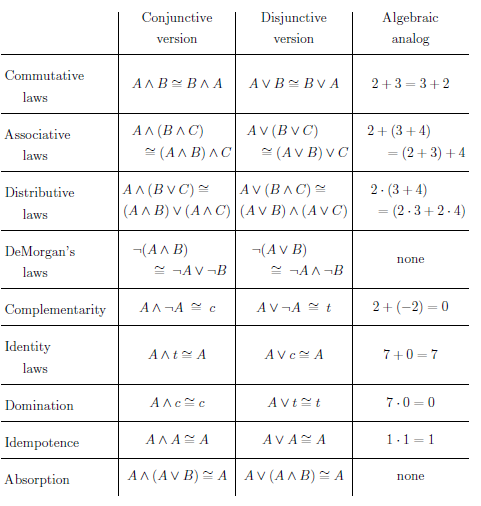
Summary
The logical equivalence we’ve covered so far is summarized in this table.
Previous topics you may want to read:
- A Gentle Introduction To Mathematics - Elementary Number Theory
- A Gentle Introduction To Mathematics - Algorithms
- A Gentle Introduction To Mathematics - Relations
- A Gentle Introduction To Mathematics - Predicates and Logical Connectives
- A Gentle Introduction To Mathematics - Implications
References:
- https://en.wikipedia.org/wiki/Logical_equivalence
- A Gentle Introduction to the Art of Mathematics by Joe Field
Thank you for reading ...


This is a test comment, notify @kryzsec on discord if there are any errors please.
Being A SteemStem Member
3.48% @pushup from @sinbad989
Being A SteemStem Member