Some Algorithm of Elementary Number Theory

What is an algorithm?

An algorithm (pronounced AL-go-rith-um) is simply a set of clear instructions for achieving some task. In computer science, it is a procedure or formula for solving a problem, based on conducting a sequence of specified actions. In mathematics, it usually means a small procedure that solves a recurrent problem.

The word algorithm is derived from the work of Al-Khwarizm. The Arabic text is lost but a latin translation, “Algoritmi de numero Indorum”.

I know, an algorithm is more properly a subject of Computer Science, but as a mathematics student, we can derive considerable benefit from the study of its mechanism.

There is a big difference between an algorithm description intended for human consumption and one meant for a computer. The former is more on text such as pseudocode while the latter is usually visual mostly in flowcharts.

An algorithm is consist of many different modules. The fundamental building algorithmic structures are for-next loops, do-while loops, if-then statements, goto statements, switch-case structures, etc.

We will use the minimal subset of the choices available.

1. Assignment statements
2. If-then control statements
3. Goto statements
4. Return

It is good to view an algorithm as something that works like a function – it takes an input as lists of parameters that describe a particular case of some general problem and creates an output as a solution to that problem.

Assignment statements

Assignment statements allow us to do all kinds of arithmetic operations. Assignments consist of evaluating some formula in the inputs and local variables and assigning that value to some local variable. A local variable does not need to be distinct, for example
X = X + 1 is a perfectly legal assignment.

If-then control statements

If-then control statements are decision makers. They control the whole flow of the algorithm, of course. They first calculate some Boolean expression, a fancy way of saying either true or false and send some program flow to different locations depending on the result.

This kind of structure is illustrated in the figure below, both in pseudocode and as a flowchart.

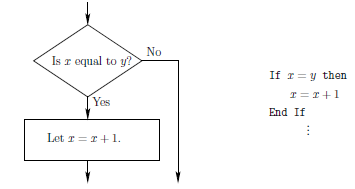
an example of an if-then statement

The two algorithmic structure that was introduced is hopefully sufficient for our purpose of introducing two algorithms that are important in elementary number theory.

Division algorithm: it is an explicit version of the process one follows to calculate a quotient and remainder using long division.

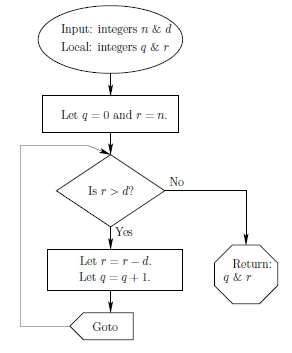
pseudocode and flowchart of the division algorithm

Notice that in the “Goto” statement its action is clear because an arrow points to the location where program flow is being redirected. Because of the possible confusion, once the algorithm becomes complicated involving multitudes of goto statements, this redirection label is now deprecated in virtually all popular programming environments.

Now let’s go to the algorithm proper.

Given a pair of integers n=27 and d=5, we let q=0 and r=27, then we compare r and d. Since r=27 is greater than d=5, it follow the yes direction and we let r = 27 - 5 = 22 , q = 0 + 1 = 1, and down to the goto statement, and compare again r and d, and so on.

This algorithm can easily be traced using Microsoft Excel, as shown in the figure below.

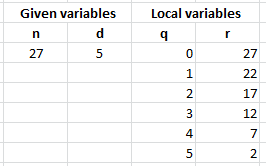
With n = qd + r and given with n =27 and d = 5 division algorithm will stop at d = 5 and r = 2

Before we move on to describe the Euclidean algorithm is would be useful if we explore two important quantities that are a property of a pair of an integer: the least common multiple (lcm) and the greatest common divisor (gcd).

• Least common multiple (lcm): usually denoted by lcm(a, b), is the smallest positive integer that is divisible by both a and b. [1]
• Greatest common divisor (gcd): usually denote by gcd(a,b) it is the largest positive integer that divides each of the integers [2]

The lcm and gcd are related by the formula:

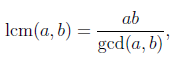
They are essentially equivalent as far as representing a computational challenge.

Euclidean algorithm: it computes the greatest common divisor (gcd) of two integers. The greatest common divisor of two numbers a and b is denoted as gcd(a,b) and is defined to the largest integer that divides both a and b evenly.

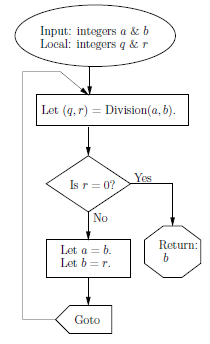
pseudocode and flowchart of Euclidean algorithm

The Euclidean algorithm depends on a rather extraordinary property of the gcd.

Suppose we want to compute the gcd of a and b, where we assume that a is greater than b. We first feed a and b to the division algorithm to find q and r such that a = qb + r. It turns out that b and r have the same gcd as did a and b. In notational form,

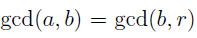
The pair b and r is smaller than the ones we started with which is nice because we’re now dealing with an easier version of the same problem.

In designing an algorithm it is important to formulate a clear ending criterion, a condition that tells you you’re done. For the Euclidean algorithm, we know we’re done when the remainder r comes out 0.

It should be noted that for small numbers, it is easier to find their lcm and gcd if we express them in terms of their prime factorizations. The gcd is the product of the primes that are common between these factorizations. The lcm, on the other hand, is the product of all the distinct primes that appear in the factorization.

Consider the number 30 and 42, we want to determine their lcm and gcd using prime factorization. The first step would be to express 30 and 40 in terms of their prime factorization but not in prime powers (factorizations don’t involve exponents).

The factorizations are 30 = 2x3x5 and 42 = 2x3x7.

For gcd, we have to determine the common number in the factorization which in our case is 2 and 3, thus gcd(30,42) = 2 x 3 = 6. The set of all primes that appear in either factorizations is {2,3,5,7} so the least common multiple is lcm(30,42) = 2 x 3 x 5 x 7 = 210.

The technique we had is not easy for numbers that involved more than 50 decimal digits because it rests a priori on the ability to find the prime factorizations of the number involved. Factoring small numbers is easy but for big numbers factorization, it becomes almost impossible. Many cryptographic schemes are based on this difficulty.

Fun fact:
Steemit blockchain is based on some cryptographic schemes. Our posting, owner, memo and active key are some representation of some big prime numbers. 👍

The intermediary between input and output is the algorithm instructions themselves and a set of so-called local variables which are used much the way scrap paper is used in a hand calculation – intermediate calculations are written on them, but they are tossed aside once the final answer has been calculated.

References

1. https://en.wikipedia.org/wiki/Least_common_multiple
2. https://en.wikipedia.org/wiki/Greatest_common_divisor
3. A Gentle Introduction to the Art of Mathematics by Joe Field
4. Data encription with big prime numbers

---

Thank you for reading ...