Aprendiendo sobre las Medidas de Tendencia Central y Dispersión

Continuando con tópicos de estadística, en este post les muestro un ejercicio resuelto de Medidas de Tendencia Central y Dispersión:

Ejercicio
Una empresa constructora tiene 2 secciones A y B. Las distribuciones de ingresos diarios de sus empleados son los siguientes:

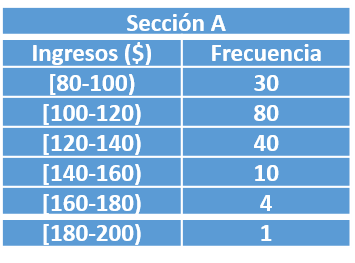
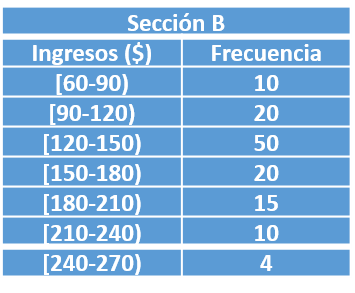
Calcular y responder lo siguiente:
a. Calcular las medidas de tendencia central y dispersión de ambas secciones.
b. ¿Cuál es el ingreso promedio de las dos secciones en conjunto?.
c. ¿Cuál de las dos secciones aporta mayores ingresos promedios a sus empleados?.

Respuesta:

a. Calcular las medidas de tendencia central y dispersión de ambas secciones.

a.1. Sección A
a.1.1. Medidas de tendencia central
Para comenzar los cálculos es necesario:

1. Sumar el total de la columna frecuencia para obtener el tamaño de la muestra, en este caso sería 165 trabajadores.
2. Calcular la marca de clase que sería el punto medio del intervalo de cada clase. Este se obtiene sumando los extremos del intervalo y dividiendo entre 2. La tabla queda de la siguiente manera:

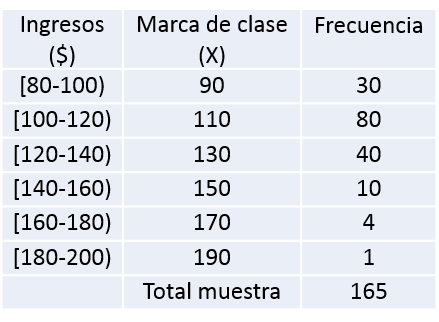
Media ponderada

Para obtener la media ponderada multiplicamos la marca de clase por la frecuencia y esta operación se realiza para cada intervalo, se suman todos esos subproductos y luego se divide entre el número de trabajadores, quedando de la siguiente manera:

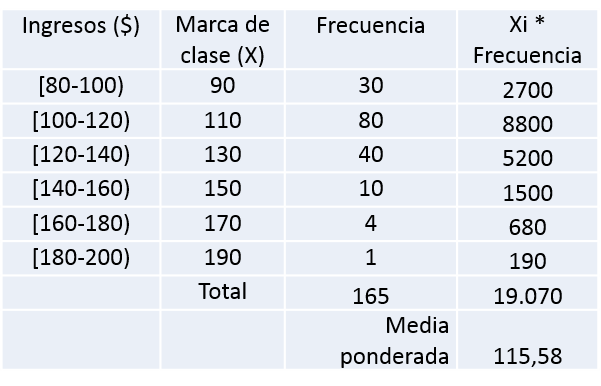
De lo anterior se desprende que la media ponderada de los ingresos de la Sección A es igual a 115,58 $.

Media ponderada Sección A = 115,58 $

Mediana
Para datos agrupados se calcula de la siguiente manera:

Md= Li + [((n/2)-Fa)/f]*c
Donde:
Md: Mediana
Li: Límite inferior del intervalo de clase de la mediana
n= Número total de datos
Fa: Frecuencia absoluta acumulada del intervalo de clase que antecede al intervalo de la mediana
F: Frecuencia absoluta del intervalo de clase de la mediana
c: Ancho del intervalo de clase de la mediana.

Lo primero que debemos hacer es identificar la clase mediana. Para esto dividimos el numero total de datos entre 2, que en este caso sería n/2 = 82,5.

Ahora necesitamos las frecuencias acumuladas, las cuales las calculamos a partir de las frecuencias absolutas dadas, corroborando que la última frecuencia acumulada nos coincida con el total de número de datos.

Luego buscamos el intervalo donde la frecuencia acumulada contenga al valor n/2 = 82,5, observándose que se ubica en el segundo intervalo identificado con el rango [100-120), por lo cual este es la clase mediana.

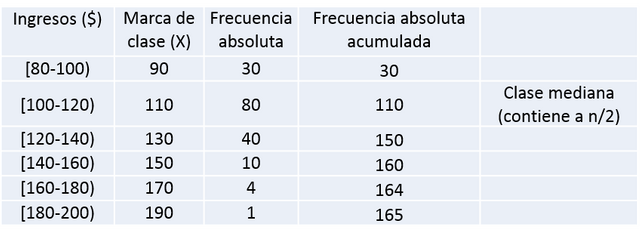
Ahora procedemos a identificar los valores que serán insertados en la fórmula de la mediana.
Md= Li + [((n/2)-Fa)/f]*c
Donde:
Md: Mediana
Li: Límite inferior del intervalo de clase de la mediana = 100
n= Número total de datos = 165
Fa: Frecuencia absoluta acumulada del intervalo de clase que antecede al intervalo de la mediana = 30
F: Frecuencia absoluta del intervalo de clase de la mediana = 80
c: Ancho del intervalo de clase de la mediana = 20

Sustituyendo en la fórmula, se obtiene que la mediana es igual a 113,12 $

Mediana Sección A = 113,12 $

Moda
Lo primero es identificar el intervalo modal, en este caso es el segundo [100-120) porque es el que tiene mayor frecuencia absoluta.

Moda= Li+ (fi – f anterior)*(ti/((fi-f anterior) + (fi-f posterior))

Donde:
Li: Límite inferior del intervalo modal
fi: frecuencia absoluta del intervalo modal
f anterior: Frecuencia absoluta anterior al intervalo modal
f posterior: Frecuencia absoluta posterior al intervalo modal
ti: Amplitud de los intervalos

En este caso:
Li: Límite inferior del intervalo modal = 100
fi: frecuencia absoluta del intervalo modal = 80
f anterior: Frecuencia absoluta anterior al intervalo modal =30
f posterior: Frecuencia absoluta posterior al intervalo modal =40
ti: Amplitud de los intervalos =20

Sustituyendo en la fórmula la moda de la Sección A es 111,11 $

Moda Sección A = 111,11 $

a.1.2. Medidas de dispersión

Rango
El rango nos da una idea general de la dispersión de la serie de datos. Mientras más grande sea el espaciamiento de los extremos de la serie, mayor será la dispersión de los datos con respecto al promedio.
Para obtener el rango, restamos el mayor valor y el menor valor, sería 200 menos 80, igual a 120. También podría obtenerse multiplicándose el número de intervalos por la amplitud de clases, esto sería 6 por 20, igual a 120; por lo tanto el rango es 120 para la Sección A.

Rango Sección A = 120 $

Varianza
Considerando datos poblacionales, la fórmula es la siguiente:
Varianza= (Sumatoria(Xi-Media Aritmética) ^2)*fi/n
Donde
Xi: Marca de clase
fi: Frecuencia absoluta de la clase
n: Número de datos

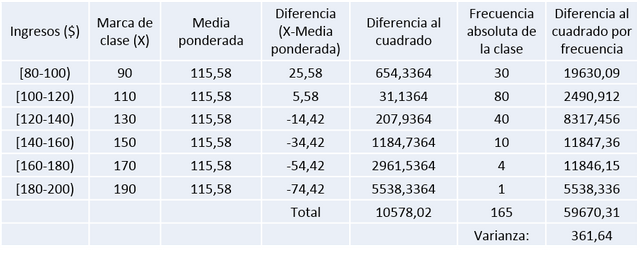
Nota: La media ponderada ya se obtuvo anteriormente, por lo cual no se repite el cálculo.
La varianza es igual a la sumatoria de las diferencias al cuadrado entre el número de datos, por lo cual la varianza de la sección A es igual a 361,64 $^2.

Varianza Sección A = 361,64 $^2

Desviación Típica o Estándar
Es la raíz cuadrada de la varianza, por lo cual la Desviación típica de la Sección A es 19,02 $

Desviación Típica Sección A = 19,02 $

Coeficiente de variación (CV)
Es igual a la desviación típica entre la media aritmética y si se quiere expresar en porcentaje se multiplica por 100.
En este caso sería (19,02/115,58) *100; por lo cual el coeficiente de variación de la Sección A es igual a 16,46%.

Coeficiente de Variación Sección A = 16,46%.
Como el coeficiente de variación es menor al 25% se deduce que los datos son homogéneos.

a.2. Sección B
a.2.1. Medidas de tendencia central
Sumando el total de la columna frecuencia obtenemos el tamaño de la muestra, en este caso sería 129 trabajadores.
Adicionalmente se obtienen las marcas de clase, promediando los extremos del intervalo.

Media ponderada
Se multiplica cada marca de clase por su frecuencia y sumando todos los subproductos, se divide por el número de trabajadores, dando el siguiente resultado:

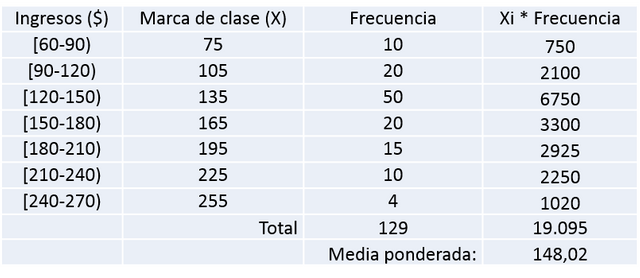
De lo anterior se desprende que la media ponderada de los ingresos de la Sección B es igual a 148,02 $.

Media ponderada Sección B = 148,02 $.
Mediana
Para datos agrupados se calcula de la siguiente manera:

Md= Li + [((n/2)-Fa)/f]*c
Donde:
Md: Mediana
Li: Límite inferior del intervalo de clase de la mediana
n= Número total de datos
Fa: Frecuencia acumulada del intervalo de clase que antecede al intervalo de la mediana
F: Frecuencia absoluta del intervalo de clase de la mediana
c: Ancho del intervalo de clase de la mediana.

Lo primero que debemos hacer es identificar la clase mediana. Para esto dividimos el numero total de datos entre 2, que en este caso sería n/2 = 64,5.

Ahora calculamos las frecuencias acumuladas, a partir de las frecuencias absolutas dadas y ubicamos la clase mediana, que el intervalo donde la frecuencia acumulada contenga al valor n/2 = 64,5, observándose que se ubica en el tercer intervalo identificado con el rango [120-150).

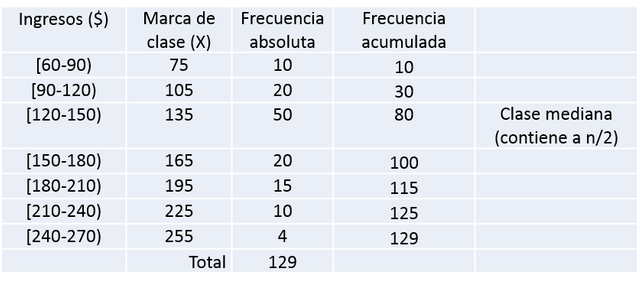
Ahora procedemos a identificar los valores que serán insertados en la fórmula de la mediana.
Md= Li + [((n/2)-Fa)/f]*c
Donde:
Md: Mediana
Li: Límite inferior del intervalo de clase de la mediana = 120
n= Número total de datos = 129
Fa: Frecuencia absoluta acumulada del intervalo de clase que antecede al intervalo de la mediana = 30
F: Frecuencia absoluta del intervalo de clase de la mediana = 50
c: Ancho del intervalo de clase de la mediana = 30

Sustituyendo en la fórmula, se obtiene que la mediana es igual a 140,70 $

Mediana Sección B = 140,70 $
Moda
Lo primero es identificar el intervalo modal, en este caso es el tercero [120-150) porque es el que tiene mayor frecuencia absoluta.

Moda= Li+ (fi – f anterior)*(ti/((fi-f anterior) + (fi-f posterior))

Donde:
Li: Límite inferior del intervalo modal
fi: frecuencia absoluta del intervalo modal
f anterior: Frecuencia absoluta anterior al intervalo modal
f posterior: Frecuencia absoluta posterior al intervalo modal
ti: Amplitud de los intervalos

En este caso:
Li: Límite inferior del intervalo modal = 120
fi: frecuencia absoluta del intervalo modal = 50
f anterior: Frecuencia absoluta anterior al intervalo modal = 20
f posterior: Frecuencia absoluta posterior al intervalo modal = 20
ti: Amplitud de los intervalos = 30

Sustituyendo en la fórmula la moda de la Sección B es 135,00 $

Moda Sección B = 135,00 $

a.2.2. Medidas de dispersión

Rango
Para obtener el rango, restamos el mayor valor y el menor valor, sería 270-60=210. También podría obtenerse multiplicándose el número de intervalos por la amplitud de clases, esto sería 7 por 30, igual a 210; por lo tanto el rango es 210 para la Sección B.

Rango Sección B = 210 $

Varianza
Considerando datos poblacionales, la fórmula es la siguiente:
Varianza= (Sumatoria(Xi-Media aritmética) ^2)*fi/n
Donde
Xi: Marca de clase
fi: Frecuencia absoluta de la clase
n: Número de datos

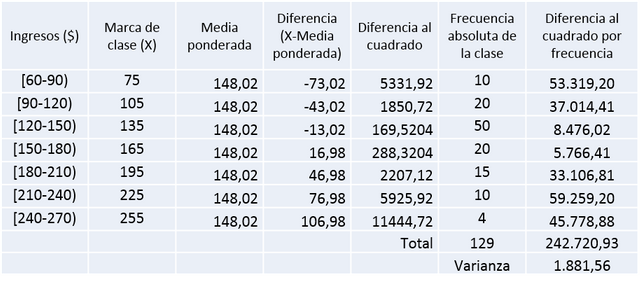
Nota: La media ponderada ya se obtuvo anteriormente, por lo cual no se repite el cálculo.
La varianza es igual a la sumatoria de las diferencias al cuadrado entre el número de datos, por lo cual la varianza de la sección B es igual a 1.881,56 $^2.

Varianza Sección B = 1.881,56 $^2

Desviación Típica o Estándar

Es la raíz cuadrada de la varianza, por lo cual la Desviación típica de la Sección B es 43,38 $.

Desviación Típica Sección B = 43,38 $

Coeficiente de variación (CV)
En este caso sería CV=(43,38/148,02) *100; por lo cual el coeficiente de variación de la Sección B es igual a 29,31%.

Coeficiente de Variación Sección B = 29,31%.

Como el coeficiente de variación es mayor al 25% se deduce que los datos son heterogéneos, o por lo menos mas heterogéneos que los de la Sección A.

b. ¿Cuál es el ingreso promedio de las dos secciones en conjunto?

Para calcular el promedio en conjunto aplicamos la misma fórmula de media ponderada pero en este caso a todos los datos de la sección A y B, quedando como se muestra a continuación:

El número de datos de la sección A y B = 165+129 = 294 trabajadores.

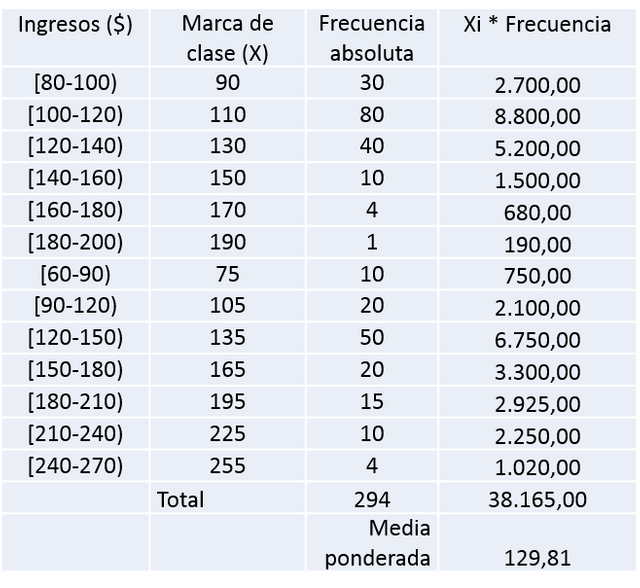
Media ponderada = Sumatoria(marca de clase * frecuencia) / número total de datos.
Media ponderada = 129,81 $

Por lo tanto 129,81 $ es el ingreso promedio de las dos secciones en conjunto.

c. ¿Cuál de las dos secciones aporta mayores ingresos promedios a sus empleados?

Para responder esta pregunta debemos comparar los promedios de ambas secciones, los cuales fueron calculados en la parte “a” del ejercicio.

Media ponderada Sección A = 115,58
Media ponderada Sección B = 148,02

Por lo tanto la Sección B es el que aporta mayores promedios a sus empleados, por presentar mayor media aritmética.

Elaborado por:
Ing. Alexandra Torres @xandra79

Si tienes alguna duda o comentario, escríbeme!

Referencias:

1. Guía didáctica “Herramientas Estadísticas. Universidad Valles del Momboy. Prof. Marilyn Briceño. Mayo, 2017.
2. Portal Educativo https://www.portaleducativo.net/octavo-basico/792/Media-moda-y-mediana-para-datos-agrupados.
3. Imágenes propias del autor.