¿SON IGUALES EL CENTRO DE MASA Y EL CENTRO DE GRAVEDAD?
Saludos para toda la comunidad de Steemit. Como se han podido enterar, mi pasión es la Física y soy Físico de profesión. Me apasiona enseñar Física a nivel universitario y escribir textos educativos de este mismo nivel (pueden ver y descargar borradores de mis textos desde mi página web www.cmc.org.ve/tsweb). Tengo especial interés por lo relacionado con la Mecánica y la Gravitación, sin embargo, incursiono en distintas áreas de la Física.

Como Físico y Profesor de Física en la Universidad, sé lo importante que es tener bien claras las definiciones utilizadas en la misma (lo mismo aplica en cualquier otra área del conocimiento). Tener claridad en las definiciones empleadas hará que la comprensión de lo estudiado sea sólida.
Es frecuente encontrar profesores a nivel de secundaria y hasta a nivel universitario que no tienen bien claras definiciones tan importantes en Física como lo son: partícula, sistema de referencia, centro de masa y centro de gravedad. Particularmente, se suele confundir el Centro de Masa y el Centro de Gravedad haciendo pensar, erróneamente, que se trata de dos denominaciones diferentes de una misma definición física.
Mis estimados Steemians, en este post, trataré de mostrar una clara definición de lo que es el Centro de Masa y el Centro de Gravedad, estableciendo una igualmente clara diferencia entre ambas definiciones. En un próximo post les hablaré de las importantísimas definiciones de partícula y sistema de referencia.
1. CENTRO DE MASA
Comencemos hablando, mis estimados Steeemians, de la definición de Centro de Masa. Esta definición es de gran importancia en el estudio de la dinámica de sistemas de partículas debido a sus muy útiles propiedades físicas.
Podemos definir de una forma clara y sencilla el Centro de Masa como sigue:
El Centro de Masa 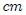 de un sistema de partículas (discreto o continuo) es el punto geométrico, dentro o fuera de él, ubicado de tal manera que al ser dotado con una masa de un sistema de partículas (discreto o continuo) es el punto geométrico, dentro o fuera de él, ubicado de tal manera que al ser dotado con una masa 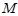 igual a la total del sistema hace que su momento lineal igual a la total del sistema hace que su momento lineal 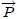 sea igual al total del mismo. Es posible decir que el Centro de Masa es el lugar donde se dupone concentrada la masa total del sistema. sea igual al total del mismo. Es posible decir que el Centro de Masa es el lugar donde se dupone concentrada la masa total del sistema. |
|---|
Bien Steemians, el objetivo ahora es determinar la posición del antes mencionado punto geométrico. Los sistemas de partículas pueden ser: discretos (este modelo considera el cuerpo formado por un número finito de partículas que están perfectamente localizadas) y continuos (este modelo considera el cuerpo formado por una distribución continua de materia, es decir, por un número infinito de partículas. Las partículas que lo forman no se pueden delimitar, llenando todo el espacio que ocupa). Pasaremos, entonces, a determinar la posición del Centro de Masa para los modelos antes mencionados.
1.1. POSICION DEL CENTRO DE MASA DE UN SISTEMA DISCRETO
Supongamos, mis estimados Steemians, que se tiene un sistema de 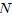 partículas de masas !
partículas de masas !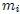 (
(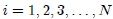 ) cuyas posiciones son referidas al origen
) cuyas posiciones son referidas al origen 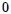 de un sistema de referencia inercial
de un sistema de referencia inercial 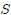 mediante los vectores de posición
mediante los vectores de posición 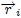 , como se muestra en la figura 1. Pensemos ahora, basándonos en la definición de Centro de Masa, en la siguiente pregunta: ¿en qué posición
, como se muestra en la figura 1. Pensemos ahora, basándonos en la definición de Centro de Masa, en la siguiente pregunta: ¿en qué posición 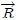 debería estar una partícula de tal manera que su masa sea igual a la total
debería estar una partícula de tal manera que su masa sea igual a la total 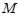 del sistema y cuyo momento lineal sea igual al total
del sistema y cuyo momento lineal sea igual al total 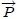 del mismo?.
del mismo?.
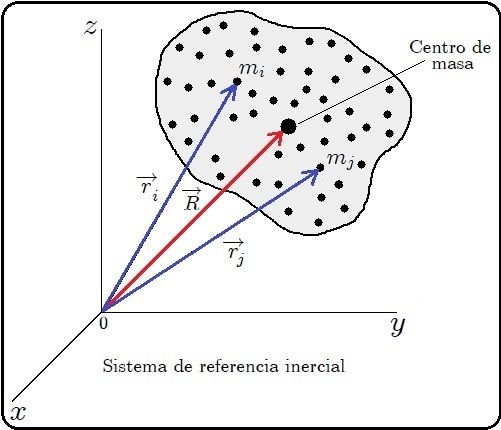
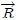 del centro de masa de un sistema discreto de
del centro de masa de un sistema discreto de 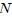 partículas (Esta imagen fue elaborada por mi persona @tsoldovieri, usando la aplicación PAINT).
partículas (Esta imagen fue elaborada por mi persona @tsoldovieri, usando la aplicación PAINT).Estimados Steemians, para responder la anterior pregunta debe expresarse matemáticamente la condición planteada en ella, lo cual podemos hacer mediante,
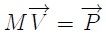
donde 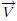 es la velocidad del punto geométrico en la posición
es la velocidad del punto geométrico en la posición 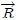 que se busca. Si cada partícula del sistema tiene un momento lineal,
que se busca. Si cada partícula del sistema tiene un momento lineal,
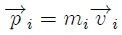
donde 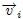 es la velocidad de cada una de las partículas, entonces,
es la velocidad de cada una de las partículas, entonces,
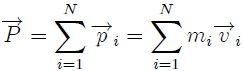
que al ser sustituido en (1) resulta en,
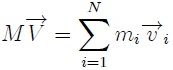
o también,
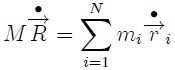
donde el punto  representa la derivada total con respecto al tiempo
representa la derivada total con respecto al tiempo 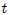 . Ahora, mis estimados Steemians, si suponemos que las masas de las partículas son constantes entonces,
. Ahora, mis estimados Steemians, si suponemos que las masas de las partículas son constantes entonces,
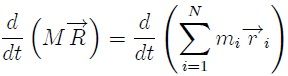
de donde,
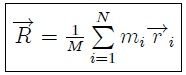
en la cual,
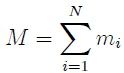
Finalmente, mis estimados Steemians, el vector 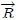 dado por (7) es el buscado vector de posición del punto geométrico que hemos denominado Centro de Masa.
dado por (7) es el buscado vector de posición del punto geométrico que hemos denominado Centro de Masa.
1.2. POSICION DEL CENTRO DE MASA DE UN SISTEMA CONTINUO
Supongamos ahora que se tiene un sistema continuo como el representado por la región 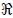 mostrada en la figura 2, de densidad
mostrada en la figura 2, de densidad 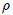 y masa
y masa 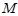 . Escojamos, mis estimados Steemians, un elemento de masa
. Escojamos, mis estimados Steemians, un elemento de masa 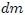 de dicha distribución. Habrán infinitos de estos elementos de masa cuyas posiciones son referidas al origen
de dicha distribución. Habrán infinitos de estos elementos de masa cuyas posiciones son referidas al origen 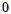 de un sistema de referencia inercial
de un sistema de referencia inercial 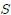 mediante los vectores de posición
mediante los vectores de posición 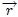 .
.
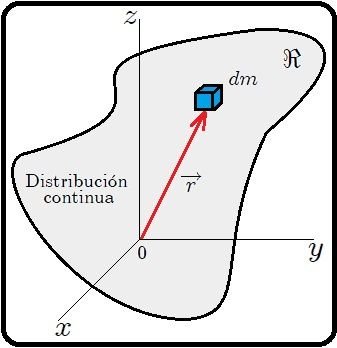
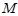 y densidad
y densidad 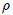 (Esta imagen fue elaborada por mi persona @tsoldovieri, usando la aplicación PAINT).
(Esta imagen fue elaborada por mi persona @tsoldovieri, usando la aplicación PAINT).Si ahora, mis estimados Steemians, pensamos nuevamente en la misma pregunta planteada en el caso del sistema discreto de partículas, mediante un procedimiento matemático análogo llegamos a que el vector de posición 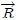 del Centro de Masa viene dado por,
del Centro de Masa viene dado por,
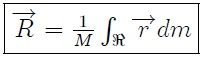
en la cual,
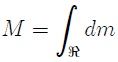
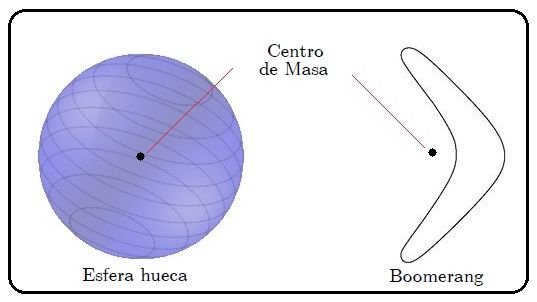
El Centro de Masa va a estar ubicado en aquella parte del sistema donde se concentre la mayor cantidad de masa y su posición no corresponde, necesariamente, con una de las partículas del sistema. Así, el centro de masa de un anillo o de una esfera hueca está en el centro geométrico de los mismos, donde no hay materia. Asimismo, el centro de masa de un boomerang está fuera de su estructura física y no dentro del material que lo forma (ver figura 3).
2. CENTRO DE GRAVEDAD
Trataremos ahora, mis estimados Steemians, con la definición de Centro de Gravedad.
El Centro de Gravedad 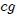 de un sistema de partículas es el punto geométrico respecto al cual las fuerzas que ejerce la gravedad sobre las diferentes partículas que constituyen al mismo, producen un momento de fuerza o torque de un sistema de partículas es el punto geométrico respecto al cual las fuerzas que ejerce la gravedad sobre las diferentes partículas que constituyen al mismo, producen un momento de fuerza o torque 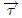 resultante nulo. Por lo tanto, es posible decir que el Centro de Gravedad es donde se supone concentrado el peso del sistema, es decir, en este punto estará el origen del vector peso total del sistema. resultante nulo. Por lo tanto, es posible decir que el Centro de Gravedad es donde se supone concentrado el peso del sistema, es decir, en este punto estará el origen del vector peso total del sistema. |
|---|
De forma análoga al Caso del Centro de Masa, mis Steemians-Lectores, planteémosnos la pregunta: ¿en qué posición 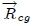 debería estar una partícula de manera tal que, respecto a la misma, las fuerzas que ejerce la gravedad sobre las diferentes partículas que constituyen al sistema, produzcan un momento de fuerza o torque
debería estar una partícula de manera tal que, respecto a la misma, las fuerzas que ejerce la gravedad sobre las diferentes partículas que constituyen al sistema, produzcan un momento de fuerza o torque 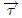 resultante nulo?. Ahora si, para responder la anterior pregunta, se expresa matemáticamente la condición planteada en ella, después de algunos cálculos se llega a la expresión,
resultante nulo?. Ahora si, para responder la anterior pregunta, se expresa matemáticamente la condición planteada en ella, después de algunos cálculos se llega a la expresión,
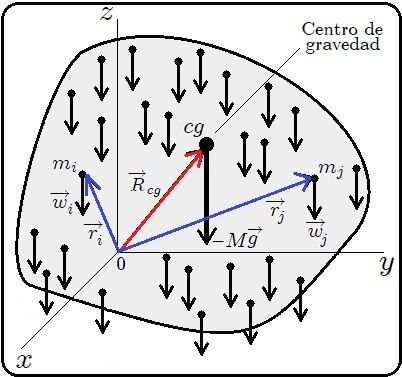
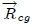 del centro de gravedad de un sistema de partículas discreto. Aquí
del centro de gravedad de un sistema de partículas discreto. Aquí 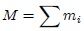 ,
, 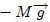 es el peso
es el peso 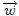 total del sistema y
total del sistema y 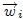 es el peso de cada una de las partículas que constituyen al sistema (Esta imagen fue elaborada por mi persona @tsoldovieri, usando la aplicación PAINT).
es el peso de cada una de las partículas que constituyen al sistema (Esta imagen fue elaborada por mi persona @tsoldovieri, usando la aplicación PAINT).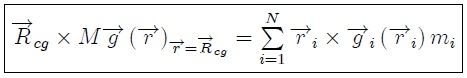
para un sistema de partículas discreto. La figura 4, mis Steemians-Lectores, muestra una representación de la posición del Centro de Gravedad para un sistema discreto de 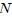 partículas. El Centro de Gravedad (al igual que el Centro de Masa) no corresponde necesariamente a una partícula del sistema. Para un sistema de partículas continuo resulta que,
partículas. El Centro de Gravedad (al igual que el Centro de Masa) no corresponde necesariamente a una partícula del sistema. Para un sistema de partículas continuo resulta que,
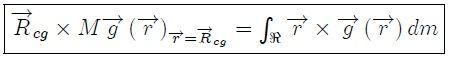
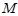 cercano a la Tierra de tamaño no despreciable respecto al de la misma, en el cual se han representado varios
cercano a la Tierra de tamaño no despreciable respecto al de la misma, en el cual se han representado varios 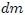 y a los cuales se les han representado las
y a los cuales se les han representado las 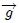 en sus respectivas posiciones (Esta imagen fue elaborada por mi persona @tsoldovieri, usando las aplicaciones PAINT y WORD).
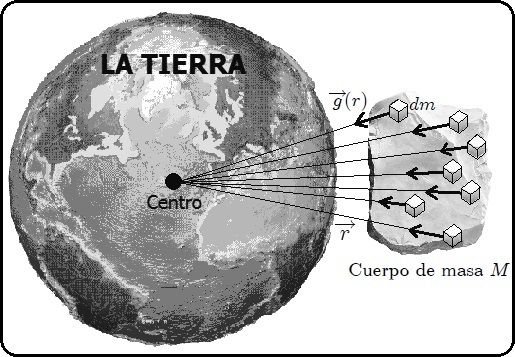
en sus respectivas posiciones (Esta imagen fue elaborada por mi persona @tsoldovieri, usando las aplicaciones PAINT y WORD).En la figura 5, mis estimados Steemians, se muestra un cuerpo continuo de masa 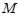 cercano a la Tierra cuyo tamaño no es despreciable con respecto al de ésta última, en el cual se han representado varios diferenciales de masa
cercano a la Tierra cuyo tamaño no es despreciable con respecto al de ésta última, en el cual se han representado varios diferenciales de masa 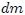 y a los cuales se les han representado las intensidades del campo terrestre
y a los cuales se les han representado las intensidades del campo terrestre 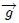 en sus respectivas posiciones. Podemos observar, mis Steemians-Lectores, que
en sus respectivas posiciones. Podemos observar, mis Steemians-Lectores, que 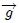 es un vector que varía en dirección de punto a punto por estar siempre dirigido al centro de la Tierra, además de que podría variar también su magnitud. En este caso, de la ecuación (12), para el cuerpo de masa
es un vector que varía en dirección de punto a punto por estar siempre dirigido al centro de la Tierra, además de que podría variar también su magnitud. En este caso, de la ecuación (12), para el cuerpo de masa 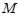 resultaría una posición para su Centro de Gravedad distinta a la posición de su Centro de Masa. Ahora, si el tamaño de este cuerpo es pequeño o despreciable con respecto al de la Tierra ocurriría que los ángulos entre los distintos vectores
resultaría una posición para su Centro de Gravedad distinta a la posición de su Centro de Masa. Ahora, si el tamaño de este cuerpo es pequeño o despreciable con respecto al de la Tierra ocurriría que los ángulos entre los distintos vectores 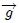 serían tan pequeños que estos vectores podrían considerarse paralelos entre sí y constantes en magnitud. En este caso, por el contrario, de la ecuación (12) resultaría una posición para el Centro de Gravedad igual a la posición del Centro de Masa. Mis Steemians-Lectores, a los efectos prácticos, esta coincidencia se cumple con precisión aceptable para todos los cuerpos que están sobre la superficie terrestre, aún para un avión 747 o un gran edificio. No sucede lo mismo con objetos astronómicos, como los planetas.
serían tan pequeños que estos vectores podrían considerarse paralelos entre sí y constantes en magnitud. En este caso, por el contrario, de la ecuación (12) resultaría una posición para el Centro de Gravedad igual a la posición del Centro de Masa. Mis Steemians-Lectores, a los efectos prácticos, esta coincidencia se cumple con precisión aceptable para todos los cuerpos que están sobre la superficie terrestre, aún para un avión 747 o un gran edificio. No sucede lo mismo con objetos astronómicos, como los planetas.
La posición Centro de Masa 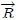 de un sistema de partículas coincide con la de su Centro de Gravedad de un sistema de partículas coincide con la de su Centro de Gravedad 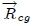 cuando el vector aceleración de la gravedad cuando el vector aceleración de la gravedad 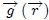 es de magnitud y dirección constante en todo el interior del mismo, es decir, cuando es de magnitud y dirección constante en todo el interior del mismo, es decir, cuando  es un vector constante. es un vector constante. |
|---|
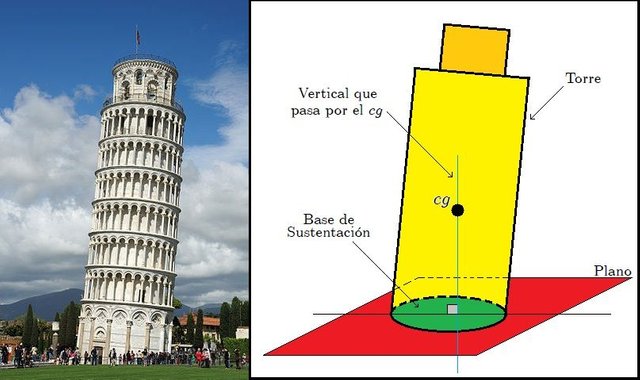
El Centro de Gravedad está relacionado con el equilibrio. Hay una ley de la Estática que dice que un cuerpo permanecerá en equilibrio siempre que la vertical que pasa por su Centro de Gravedad caiga dentro del polígono de apoyo o base de sustentación del mismo (la base o polígono de sustentación es la figura geométrica que se forma en el plano perpendicular a la vertical que pasa por el Centro de Gravedad, al unir los puntos de contacto del cuerpo con el mismo). Por ejemplo, la torre inclinada de Pisa (vean la figura 6) está en equilibrio estable, porque ha sido construida con materiales muy pesados hasta la 1/4 parte y luego más y más livianos yendo hacia arriba. De esta manera se ha bajado considerablemente el centro de gravedad de la torre, y la vertical que arranca de dicho centro cae todavía muy dentro de la base de sustentación delimitada por los cimientos.
Esto no termina aquí mis muy estimados Steemians, existe una definición matemática denominada Centroide que también suele confundirse con la de Centro de Masa y Centro de Gravedad.
El Centroide o Baricentro es un punto que define el centro de un cuerpo geométrico (no físico), es decir, es el centro de simetría. |
|---|
Hay que hacer incapié, mis Steemians-Lectores, en que el Centroide o Baricentro se refiere a cuerpos puramente geométricos, es decir, no se refiere a cuerpos materiales ya que son cuerpos sin masa. Todo cuerpo material está definido por un cuerpo geométrico que encierra toda la masa del mismo. La posición del centro de masa de un cuerpo material coincide con la posición del centroide del cuerpo geométrico que lo define si el primero es homogéneo. Si un cuerpo material es simétrico y homogéneo se puede hallar su centroide fácilmente. Por ejemplo, para el caso de una varilla o segmento homogéneos, el centroide es el punto medio y para una esfera o una circunferencia homogéneas, el centroide también se encuentra en su centro geométrico. El el caso de un triángulo, se encuentra en la intersección de las medianas (las medianas son las tres rectas que unen cada vértice del triángulo con el centro del lado opuesto).
3. PROPIEDADES DEL CENTRO DE MASA
Mis estimados Steemians-Lectores, el Centro de Masa posee varias propiedades que lo hacen de extrema importancia en la Física, las cuales mencionaré sin demostración (por estar fuera del objetivo del presente post):
- Es un punto geométrico que no tiene por qué corresponderse con la posición de una partícula del sistema.
- Si existe una distribución homogénea de la masa, su posición está contenida en los elementos de simetría del sistema. Si el sistema tiene un plano o un eje de simetría éste contiene al centro de masa y si posee un centro de simetría, éste será directamente el centro de masa.
- Es independiente del sistema de referencia inercial empleado para localizarlo. Sólo depende de la masa de las partículas y de sus posiciones relativas entre sí.
- Dinámicamente se comporta como si en él estuviera aplicada la resultante de las fuerzas externas al sistema, moviéndose como una partícula cuya masa es la masa total del sistema. La aceleración del centro de masa coincide con la aceleración del sistema. Es esta la propiedad que permite reducir el estudio de la dinámica de un sistema de partículas al de una partícula.
- Si las fuerzas externas que actúan sobre un sistema tienen una resultante y un momento nulos, el centro de masa se mueve con movimiento rectilíneo y uniforme. Las fuerzas internas no modifican el movimiento del centro de masa en el caso de que las mismas cumplan con la tercera ley de Newton.
- Si se toma el centro de masa como origen de referencia, la cantidad de movimiento del conjunto de partículas es siempre nula.
- El movimiento más general que puede tener un sistema de partículas se puede reducir a un movimiento de traslación de su centro de masa más una rotación alrededor de un eje que pasa por dicho punto.
De las anteriores propiedades, la 4 es de vital importancia. Esta propiedad, mis Steemians-Lectores, nos dice nada más y nada menos que el Centro de Masa se comporta como lo haría una partícula real de masa igual a la masa total 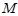 del sistema, pues cumple con la segunda ley de Newton. Permite convertir un sistema de partículas en uno dinámicamente equivalente de una partícula, lo cual simplifica enormemente el estudio. del sistema, pues cumple con la segunda ley de Newton. Permite convertir un sistema de partículas en uno dinámicamente equivalente de una partícula, lo cual simplifica enormemente el estudio. |
|---|

Lo anterior lo podemos observar, mis Steemians-Lectores, en la figura 7. En esta figura les muestro el lazamiento con ángulo de elevación de un pin de bolos girando. Su trayectoria no es uniforme, pues su movimiento es tambaleante; parece que cabecea por donde quiera. Sin embargo, el Centro de Masa del pin segue una trayectoria uniforme (una parábola) como lo haría una partícula lanzada de la misma forma.
CONCLUSIONES
Mis estimados Steemians-Lectores, depués de todo lo anterior se pueden establecer las siguientes conclusiones:
- El Centro de Masa y el Centro de Gravedad no son iguales en general. Sólo coinciden cuando el tamaño del sistema al que se le determina es pequeño con respecto al tamaño del sistema que genera el campo gravitacional. Como los sistemas que manejamos en los laboratorios y los sistemas que nos rodean son pequeños con respecto al tamaño de la Tierra, entonces la posición del Centro de Masa y el Centro de Gravedad coinciden. Siempre debemos tener presente lo anterio a la hora de tratar estos temas mi Steemians-Lectores.
- El Centro de Gravedad depende del campo gravitacional en el que está inmerso el sistema, siendo dependiente del tamaño de la fuente que lo genera. Lo anterior no ocurre con el Centro de Masa.
- El Centro de Gravedad está relacionado directamente con el equilibrio del sistema y el Centro de Masa está relacionado con la dinámica del mismo, permitiendo reducir su estudio al de una partícula virtual cuya masa es la total del sistema y que obedece las Leyes de la Mecánica Newtoniana de una partícula.
BIBLIOGRAFIA RECOMENDADA
Soldovieri, Terenzio. INTRODUCCION A LA MECANICA CLASICA. 1era edición (borrador), 2018. Página 216. Puede descargarse desde mi web http://www.cmc.org.ve/tsweb/
Halliday, D. & Resnick, R.(Walker, J.). FUNDAMENTALS OF PHYSICS. John Wiley & Sons, Inc., 10th edition, 2014. Página 215 y 330.
Serway, R. A. y Jewett, J. W. FISICA, volumen 1. Cengage Learning Editores,S.A. de C.V., 7ma edición, 2008. Página 245.
Giancoli, D. C. FISICA, volumen 1. Pearson Educación, México, 4ta edición, 2008. Página 230.
Alonso, M. & Finn, E. J. FISICA - MECANICA, volumen 1. Fondo Educativo Interamericano, S.A., 1970. Página 68.
Sears, F. W.; Zemansky, M. W.; Young, H. D. & Freedman, R. A. FISICA UNIVERSITARIA, volumen 1. Pearson Educación de México, S.A. de C.V., México, 12da edición, 2009. Página 266.
Tipler, P. A. & Mosca, G. FISICA PARA LA CIENCIA Y LA TECNOLOGIA - MECANICA, OSCILACIONES Y ONDAS, TERMODINAMICA, volumen 1. Editorial Reverté, S. A., 5ta edition, 2005. Página 202.
Mencuccini, C. & Silvestrini, V. FISICA I, parte prima. Liguore Editore, 1988. Página 206.

Estimados Steemians-Lectores, espero que la anterior información les sea de mucha utilidad y que definitivamente les permitan diferenciar entre la definición de Centro de Masa y Centro de Gravedad. Si tienen preguntas, no duden en hacérmelas llegar pues, con mucho gusto, les atenderé. Hasta mi próximo post ¡Saludos a todos! 😁.
Si deseas leer más artículos científicos de buena calidad, no pierda el tiempo, visite la etiqueta #steemstem. Es un gran proyecto que ha crecido enormemente en los últimos meses, con el fin de promover altos puestos a publicaciones científicas
Unete al canal de @steemstem. También puedes visitar el blog @steemstem y obtener mas información.


Realmente los términos físicos son usados en el lenguaje coloquial de manera ambigua y a veces de forma arbitraria, por lo que el aporte que haces a la comunidad #stem-espanol es de gran importancia para tener un acertado conocimiento de esta ciencia. Excelente publicación mi estimado @tsoldovieri
Así es @iamphysical, ocurre muy a menudo. Gracias por tu comentario y apoyo. Seguiré publicando artículos de este estilo, entre otros, que contribuyan al fortalecimiento de la comunidad #stem-espanol. Saludos.
Siendo un SteemStem Estados
Se hace tan fácil todo cuando alguien realiza una excelente explicación.
Tal vez, si saltamos llevando nuestro cuerpo al aire... y perdemos el centro de gravitación, nos caeríamos por haber perdido el equilibrio, y toda la masa cruda va directo al piso... errores que se pagan por no coordinar el movimiento entre la masa y el centro de gravedad.
Saludos mi estimado profesor @tsoldovieri
Caramba amigo @henrycalu, gracias por tu comentario y apoyo. Me alegra y me gratifica mucho que te haya gustado mi post. Siempre trato de hacer el mayor esfuerzo en la realización de mis posts. Nuevamente, muchas gracias. Saludos.
Siempre es grato leer sus publicaciones: poseen una excelente y justa información, con sus oportunos gráficos e ilustraciones que acompañan al texto con la precisa posición dentro del mismo. Sencillamente confiable y se entiende perfectamente.
Usted es una guía a seguir como profesor.
Gracias Terenzio Soldovieri @tsoldovieri por estar ahí compartiendo sus conocimientos.
Muchísimas gracias por tu comentario y apoyo amiga @maria1989.
¡Saludos!
Sin lugar a dudas un tratamiento magistral del tema @tsoldovieri. Una pregunta: ¿podríamos generalizar que para un sistema pequeño con respecto al tamaño de la tierra la famosa fórmula Ycg= (A1y1+A2y2…..An*yn)/(At), el resultado que arroja coincide tanto para el centro de gravedad, centro de masa y centroide? Por ejemplo aplicado este hecho a la planta de una edificación, la sección transversal de una viga.
Es interesante saber que hay una diferencia conceptual importante, pero ¿podríamos decir que para sistemas pequeños con respecto al tamaño de la tierra su valor coincide?
Una de las aplicaciones que le damos a este concepto en la dinámica estructural, es en el establecimiento del modo de vibración torsional, que se da cuando el centro de rigidez se encuentra desfasado del centro de masa.
Para complementar en una edificación, las masas las concentramos en las losas, que denominamos “diafragmas”, y por lo general su centro de masa lo ubicamos en su centro geométrico. Por eso me encantaría tener su feedback con las pregunta realizadas al principio.
Saludos y nuevamente felicidades @tsoldovieri
Muchísimas gracias por tu excelente comentario y apoyo @eliaschess333. Es obvio que te gustó mi post, lo cual produce en mi mucha alegría y ganas de seguir trabajando duro en pro de la ciencia, de esta comunidad #stem-espanol y #steemstem, y de la comunidad Steemit en general. En principio, para que coincidan, la ecuación que me presentas debe reducirse a aquella que proporciona la posición del Centro de Gravedad en el límite de cuerpos cuyo tamaño es pequeño con respecto al de la Tierra. Con el Centro de Masa no importa este tamaño, pues es independiente del campo gravitacional. Es por esto que es la posición del Centro de Gravedad la que se reduce a la del Centro de Masa en este límite y no en el inverso sentido. Me podrías dar una referencia bibliográfica o una dirección web donde pueda ver la ecuación que me presentaste con su teoría correspondiente?. Es que como la presentas no logro identificarla. Espero tu respuesta para, con mucho gusto, seguir intercambiando conocimientos. Nuevamente, muchísimas gracias. Ya te estoy siguiendo, sígueme si es de tu agrado 👍 .Saludos.
Saludos @tsoldovieri agradecido por tu respuesta, me permite desarrollar un sentido crítico hacia estos conceptos. Puedes consultar el siguiente enlace:
https://steemit.com/stem-espanol/@eliaschess333/estudio-del-comportamiento-de-vigas-de-concreto-armado-de-seccion-rectangular-tomando-como-referencia-los-estados-dese
En ese artículo específicamente en el tópico "estimación del momento de agrietamiento"utilizo esta fórmula para definir la posición del eje neutro, y en conjunto a la aplicación del teorema de Steiner, calculo la inercia de la sección. Ahora bien, cuando se hacen los cálculo del centro de gravedad en una planta de una edificación, este viene definido por las coordenadas “x,y” estimadas con la aplicación de esa ecuación, respetando la dirección que se estudie. El cálculo del centro de gravedad para una planta rectangular de dimensiones “Lx * Ly” se resumiría en establecer como Lx/2 y Ly/2, que es una simplificación de la fórmula, dado que como se tiene una sola área esta se simplifica.
Te adjunto una captura de imagen del libro “Manual de Fórmulas Técnicas. Autores: Kurt Gieck y Reiner Gieck. Editorial: Alfaomega. Edición N°30”.
Nuevamente gracias por tu respuesta y saludos cordiales @tsoldovieri!
Saludos amigo @eliaschess333. Disculpa la tardanza en responder tu pregunta. La ecuación que tu me presentas no es más que la ecuación para el cálculo de Centroides. En fin, como lo dije en mi post, los Centroides sólo se refieren a cuerpos geométricos (cuerpos sin masa alguna unidimensionales, bidimensionales o tridimensionales). Son cuerpos meramente geométricos, es decir, sin masa. Por esta razón en las ecuaciones para el cálculo de la posición del Centroide no aparece, por ningún lado, la masa.
Claro está, todo cuerpo físico (cuerpos con masa) está definido por un cuerpo geométrico, por ejemplo: un balón de fútbol estaría definido geométricamente por una esfera, una lámina cuadrada plana (de espesor despreciable) estaría definida geométricamente por un cuadrado y, en general, cualquier cuerpo físico de forma irregular estaría definido por un cuerpo geométrico formado por la superficie del cuerpo físico correspondiente. En los casos particulares en que el cuerpo físico sea homogéneo (su masa está distribuida uniformemente) la posición de su Centro de Masa coincide con la del Centroide del cuerpo geométrico que lo define, como bien lo dije en el post. En los cuerpos que no son homogéneos (como, en general, lo son aquellos involucrados en las construcciones), la posición del Centro de Masa no coincide con la posición del Centroide del cuerpo geométrico que lo define. Cuando tu posicionas el Centro de Masa de las losas en su centro geométrico (o Centroide) estás suponiendo que cada losa es completamente homogénea, siendo verdaderamente no homogéneas. Sin embargo, supongo que debido a su pequeño tamaño con respecto a la edificación entera, es posible suponer que las losas son homogéneas sin que esto introduzca errores significativos en los cálculos involucrados en el estudio de la edificación. La no coincidencia de la posición del Centro de Masa y del Centroide de un cuerpo nada tiene que ver con el campo gravitacional (en las ecuaciones no aparece la intensidad del campo g, o aceleración debida a la gravedad, por ningún lado), sólo se debe a la inhomogeneidad del cuerpo físico estudiado. La posición del Centro de Gravedad de un cuerpo físico coincide, como lo dije en el post, con la posición del Centro de Masa cuando el cuerpo físico estudiado tiene un tamaño pequeño comparado con el cuerpo que genera el campo gravitacional que, en nuestro caso, es la Tierra. Para todos los cuerpos sobre la superficie terrestre (incluyendo los grandes edificios, las grandes represas, las grandes montañas, etc.) la posición del Centro de Masa y el Centro de gravedad coinciden, pues todos ellos son minúsculos con respecto al tamaño de la Tierra. Para que esto no ocurra tendrían que ser cuerpos de tamaño comparable a la Tierra, es decir, enormes como la Luna.
En conclusión:
Espero que haya podido aclarar tus dudas amigo @eliaschess333. Es todo un placer para mí tener este tipo de interacción. Para cualquier otra duda, aquí estaré siempre a la orden. Una vez más, disculpa la tardanza.
¡Saludos!
Estimado @tsoldovieri, impresionado por la calidad de su respuesta, es usted un maestro. Agradecido por la asesoría brindada. Saludos, y muchos éxitos; y que su sabiduría se expanda en todos los estudiantes que tienen la dicha de ver clases con usted y los que tenemos la dicha de recibir sus consejos. Saludos amigo, estaré atento a tus publicaciones!!!
Gracias por los halagos. Estaré aquí siempre presto a servir. Me alegra mucho que haya podido resolver tus interrogantes amigo @eliaschess333. Creo que mi próximo post (el de esta semana) lo dedicaré a aclarar la definición de partícula material o cuerpo puntual en Mecánica Clásica, el cual formará parte de una sección en uno de los capítulos del libro de Mecánica Clásica que estoy escribiendo. En mi página http://www.cmc.org.ve/tsweb puede ver y descargar los borradores de mis libros. Gracias nuevamente. Saludos.
Sin duda alguna la física es un carrera impresionante y diga de admiración, sobre todo bastante compleja!!
Que bueno que estudie medicina jeje
La física es, en extremo, interesante. Es, para mi, una hermosura de ciencia 😁. Gracias por tu comentario y apoyo. Ya te estoy siguiendo, sígueme si es de tu agrado. Saludos. 😉 😁
Se que no es muy inteligente lo que voy a decir pero una sola palabra para expresar este contenido: "Maravilloso"
Muchas gracias @carloserp-2000. Gracias por tu comentario. Siempre trato de plasmar mi experiencia como profesor en mis posts. Siempre tratando de ser aún mejor y tratando de expresar mis contenidos de la forma más clara y sencilla posible. Nuevamente, gracias. Saludos.
Amigo @carloserp-2000. Tengo una pequeña duda. El que yo reedite este post para corregir algunas palabras que quedaron mal escritas ¿afectaría los votos que ya tiene? ¿tu lo hiciste alguna vez?. Gracias.
Muy informativo tu post hermano, saludos.
Muchísimas gracias hermano @rnunez09. Saludos.
Muy hermoso trabajo, estimado Colega. Cada vez superándote. Saludos
Muchas gracias por su comentario y apoyo mi muy hermosa colega @emily61. Saludos.
Jaaaaaaaa tendria que pasarme una semana leyendo tu post para entender los esquemas completitos que aquí se abordan.
Gracias por compartir tan bello post de ciencia.
😁 gracias por tu comentario y apoyo amigo @galberto. Seguiré trabajando duro. Saludos.