ABORDAJE DIDÁCTICO DEL CONCEPTO DE ENERGÍA DESDE EL ENFOQUE DE LA INGENIERÍA SISMORESISTENTE. CASO: SISTEMAS QUE SE COMPORTAN ELÁSTICAMENTE SOMETIDOS A UNA VIBRACIÓN FORZADA ARMÓNICA. PARTE I

Saludos apreciados lectores de la plataforma de #steemit, y muy especialmente a la comunidad científica de #stem-espanol. Basado en mi lema de “hacer docencia más allá de los muros del aula”, este artículo inicia un interesante proceso de estudio, donde estaré profundizando sobre el concepto de energía con un enfoque sismoresistente. En aras de hacer didáctico este proceso de aprendizaje, comenzaremos el estudio con excitaciones armónicas que experimenta un sistema de un grado de libertad, lo que permitirá afianzar muchos conceptos de importancia, claves para abordar excitaciones de mayor complejidad, como por ejemplo, la representada por un sismo. Disfruten de este post, hecho con mucho cariño y esfuerzo.

@eliaschess333

INTRODUCCIÓN

El tema de trabajo y energía, permite la comprensión de muchos fenómenos físicos que ocurren en nuestro alrededor. A continuación lo aplicaremos en sistemas estructurales de un grado de libertad, que vibran como consecuencia de que están sometidos a una fuerza externa, representada en este estudio por una excitación de tipo armónica. He tenido el placer de compartir con ustedes queridos lectores, varios artículos donde he trabajado el tema de vibración forzada armónica, los cuales te invito a consultarlos (ver referencias N°05 y N°06). También es recomendable, si te inicias en el estudio de estos temas, repasar conceptos bases de la Dinámica Estructural, por lo que es oportuno en tal caso, que revises la referencia N°07.

Imagen N°01: una visión global de las ideas a estudiar

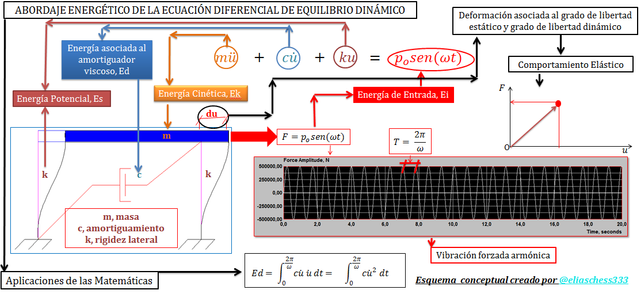
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El gráfico correspondiente a la fuerza armónica, proviene de la herramienta computacional NONLIN V 7.14.

En este trabajo, haremos uso de las aplicaciones de las matemáticas para abordar la ecuación diferencial de equilibrio dinámico desde un enfoque energético, tal como se aprecia en el esquema conceptual de la imagen N°01, lo cual nos prepara en nuestra formación como ingenieros sismoresistentes, hacia el hecho de afianzar criterios de importancia práctica, acerca del balance energético que existe, entre la energía de entrada (fuerza externa), y las energías asociadas a las propiedades intrínsecas de las estructura, como lo son, su rigidez “K”, amortiguamiento “c” y masa “m”. Conviene señalar que en esta primera entrega, las deducciones realizadas serán base para interpretaciones de carácter cualitativo; en la parte dos de este trabajo, comenzaremos a realizar ejemplos de carácter cuantitativo, con ayuda de la herramienta computacional NONLIN V 7.14.

DELIMITACIÓN DE LA TEMÁTICA A ESTUDIAR

Son muchos aspectos que es necesario delimitar, por lo que te recomiendo amigo lector los tengas presentes a lo largo de la lectura; de igual manera en el desarrollo de la misma, indicaré cuando sea pertinente revisar nuevamente este tópico. Primeramente vale destacar que estaremos trabajando con sistemas estructurales idealizados con un grado de libertad dinámico y un grado de libertad estático, que se comportan elásticamente y que se encuentran sometidos a una vibración forzada armónica (ver imagen N°01). Debido a este comportamiento elástico, es el amortiguamiento viscoso el encargado de disipar la energía de entrada a la estructura. Te invito a que revises las referencias N°04, N°05 y N°06, para que te familiarices con estos conceptos, que dan la base para adentrarse a aplicaciones de mayor profundidad, como las que se abordan en este trabajo.

En este orden de ideas, la ecuación diferencial que rige el equilibrio dinámico del sistema está representada por:

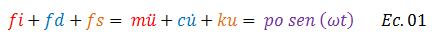
Aquí considero oportuno traer a colación un gráfico donde por medio del principio de D’Alembert se ilustra la interacción entre la fuerza que representa la excitación externa, y aquellas encargadas de devolver a la estructura a su estado de reposo, conocidas como fuerzas inerciales “fi”, de amortiguamiento “fd” y de restitución elástica “fs”.

Imagen N°02: ilustración didáctica de las fuerzas que intervienen en el equilibrio dinámico del sistema

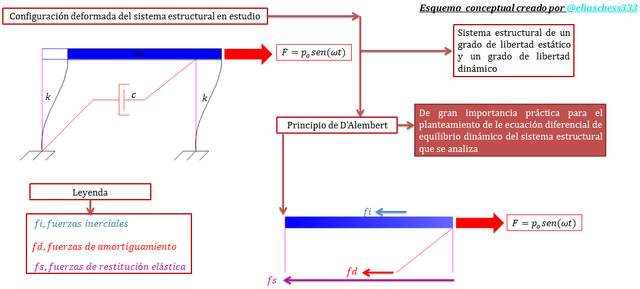
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El sistema estructural y el diagrama de cuerpo libre, fueron elaborados con el programa AutoCAD 2010.

En lo que respecta a la excitación externa, esta está representada por una fuerza armónica (término resaltado en color “púrpura” en la ecuación N°01), y el comportamiento del sistema estructural en términos de desplazamiento lo idealizaremos en fase con la fuerza aplicada (el sistema se desplaza en la misma dirección de aplicación de la fuerza; en futuras publicaciones, profundizaré en la noción del ángulo de fase “ϕ”, dado que este nos proporciona más ideas para comprender la interacción en términos de desplazamiento entre la fuerza externa y la conducta del sistema estructural), por lo que según Chopra (2014):

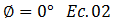
Esta delimitación será de gran ayuda en el tópico concerniente a “ABORDAJE DE LA ECUACIÓN DIFERENCIAL DE EQUILIBRIO DINÁMICO DESDE UN ENFOQUE ENERGÉTICO”. Es necesario acotar para que se dé la condición plasmada en la ecuación N°02, que el cociente que resulta de dividir el periodo de la excitación externa “T” con el periodo natural “Tn” ha de ser mayor que uno, lo que es un indicativo que la fuerza varía lentamente (ver ref. N°05).

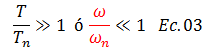
De esta ecuación se desprende que el cociente del término resaltado en color “rojo” para el caso en estudio, será un valor muy pequeño, y esto será de ayuda para hacer una serie de simplificaciones en los tratamientos matemáticos que siguen más adelante. Adicionalmente cuando se está en presencia de este caso, se tiene que la deformación máxima dinámica “uo”, tiende a ser igual a la deformación máxima estática “ust”.

DESARROLLO MATEMÁTICO PARA SUSTENTAR UNA FORMA ALTERNATIVA DE PRESENTAR LA SOLUCIÓN ANALÍTICA DE LA ECUACIÓN N°01

En la referencia N°06, desarrollamos la solución analítica de la ecuación diferencial de equilibrio dinámico del sistema estructural sometido a una vibración forzada armónica, cuyo resultado enfocado a la respuesta estacionaria “solución particular” es el siguiente:

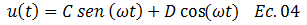
Donde las constantes de integración están representadas por:

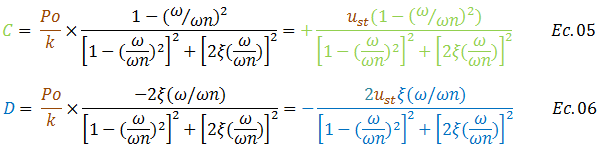
Sustituyendo las ecuaciones N°05 y N°06 en la ecuación N°04, se tiene:

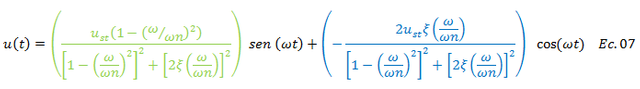
Rescribiendo:

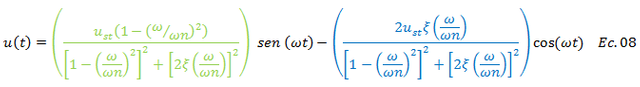
Ahora bien, surge la necesidad de llevar la ecuación N°08 a una expresión como la representada por la ecuación N°09, con la finalidad de facilitar el abordaje matemático del concepto de energía:

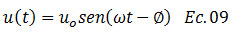
El término “uo” de la ecuación N°09 corresponde a la máxima deformación dinámica que se puede dar en el sistema estructural, y se asocia con el factor de amplificación dinámica “Rd” y la deformación estática máxima “ust”, lo cual se demuestra en el desarrollo de las ecuaciones que van de la número 10 a la número 21, y que se sustentan en las ideas plasmadas en la imagen N°03. En este sentido, la ecuación N°08 puede ser tratada con un artificio matemático, donde los términos resaltados en color “verde” y “azul” permiten construir un triángulo rectángulo:

Imagen N°03: artificio matemático para la presentación alternativa de la ecuación N°08

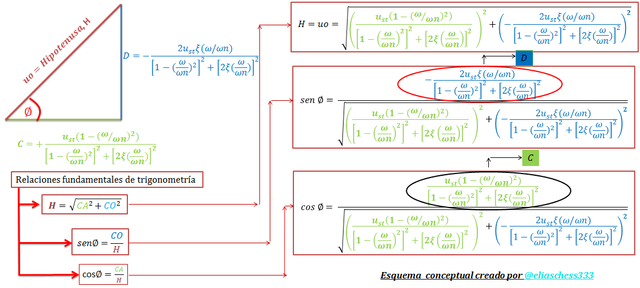
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.

De acuerdo a las expresiones para “sen ϕ” y “cos ϕ” en la imagen N°03, podemos plantear una forma alternativa de presentar la solución analítica de la ecuación diferencial, consistente en primera instancia en despejar “C” y “D” de dichas expresiones, representativas de los términos resaltados por los óvalos de colores “negro” y “rojo” respectivamente:

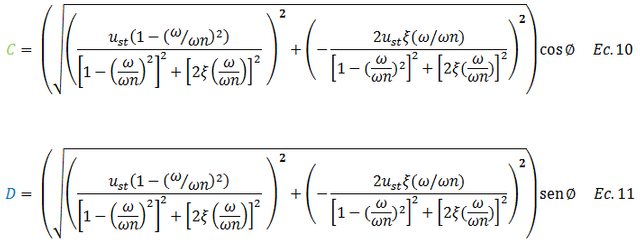
Realizada esta operación, sustituimos en la ecuación N°04 las expresiones obtenidas para “C” y “D”, desarrollando al mismo tiempo una serie de operaciones matemáticas que permiten sustentar que la ecuación N°09 es una forma alternativa de presentar la solución de la ecuación diferencial de equilibrio dinámico del sistema (ver Ec. 01), siendo esto uno de los retos previos que tenemos que superar para así adentrarnos en el tema energético como tal.

Estas ideas se plasman didácticamente en el esquema conceptual de la imagen N°04:

Imagen N°04: desarrollando una forma alternativa de presentar la ecuación N°04

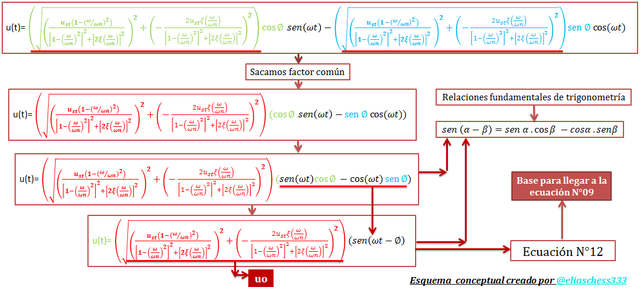
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.

El término representativo de “uo” en la ecuación N°12 (ver imagen N°04), amerita un tratamiento matemático especial, por lo que es oportuno presentarlo a continuación:

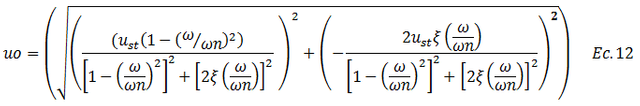
Eliminamos paréntesis y aplicamos reglas de potencia de la siguiente forma:

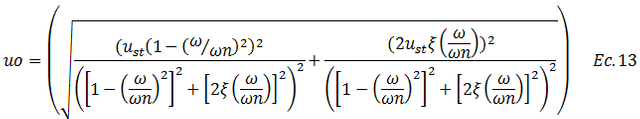
Realizamos la respectiva suma de fracciones:

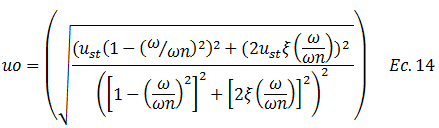
La ecuación N°14 aplicando leyes de radicación queda de la siguiente manera:

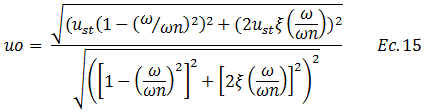
Reescribimos al numerador:

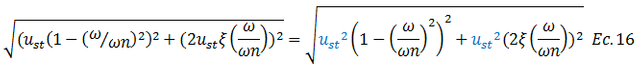
El término resaltado en color “azul” en la ecuación N°16 es factor común, el cual al mismo tiempo le podemos sacar su raíz cuadrada:

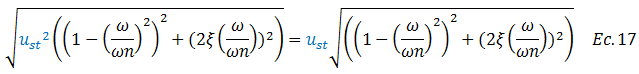
Rescribimos la ecuación N°15, planteando el numerador de conformidad a la ecuación N°17:

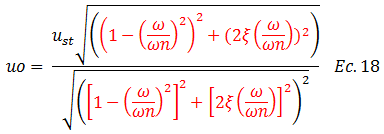
El término resaltado en color “rojo” estratégicamente lo llamaremos “x”, surgiendo lo siguiente:

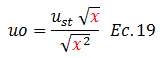
Aplicando propiedades de raíces:

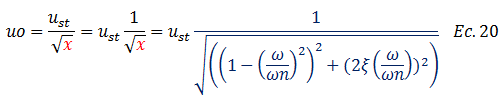
El término resaltado en color “azul” corresponde al factor de amplificación dinámica “Rd”:

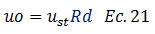
Concluyéndose así que la ecuación N°09, es una forma simplificada de presentar la solución analítica de la ecuación diferencial de equilibrio dinámico, sustentada esta alternativa con los desarrollos matemáticos realizados anteriormente. Al mismo tiempo esta ecuación es base para el abordaje del problema desde un enfoque energético, aspecto fundamental de este trabajo.

ABORDAJE DE LA ECUACIÓN DIFERENCIAL DE EQUILIBRIO DINÁMICO DESDE UN ENFOQUE ENERGÉTICO

En primer lugar considero oportuno que repasemos conceptos básicos de trabajo y energía, a través de una sencilla introducción al cálculo integral, fundamental en el abordaje que se desea realizar. En este orden de ideas, según Fierro y García (2005), el trabajo realizado por una fuerza está dado por la siguiente expresión:

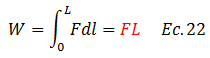
Lo reflejado en la ecuación N°22 se complementa con la idea que expone Giek y Giek (2003), donde señalan que:

Si una fuerza de 1 N se ejerce a lo largo de la trayectoria de 1 m, esta efectúa un trabajo (energía) de 1N.1m =1 joule (J)

Basado en lo anteriormente expuesto, los conceptos de trabajo y energía van de la mano. Ahora extrapolemos estas ideas al campo de la ingeniería sismoresistente, donde “F” viene a estar representada por fuerzas inerciales (fi), fuerzas de amortiguamiento (fd), fuerzas de restitución elástica (fs), fuerzas externas y “dl” por “du”, que corresponde al diferencial de desplazamiento de la masa con respecto a la base, en consonancia con el grado de libertad del que se dispone; utilicemos el esquema conceptual de la imagen N°05, para una mejor comprensión de los aspectos señalados:

Imagen N°05: extrapolación del principio de trabajo y energía al caso en estudio

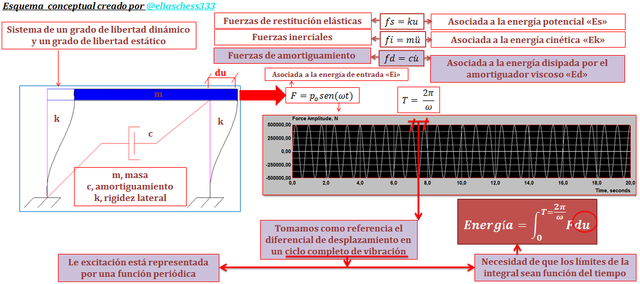
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El pórtico fue elaborado con el programa AutoCAD 2010. El gráfico resaltado en color rojo, proviene de la herramienta computacional NONLIN V 7.14.

Se tiene entre otros aspectos una forma alternativa de hacer el planteamiento de la integral, esencial para abordar la ecuación N°01 desde un enfoque energético. No obstante, el diferencial resaltado por el óvalo de color “rojo” (ver imagen N°05), no corresponde precisamente a un diferencial de tiempo “dt”; por lo que es necesario hacer un artificio, consistente en multiplicar y dividir por “dt”:

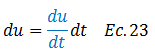
El término resaltado en color “azul” corresponde a la derivada del desplazamiento con respecto al tiempo, lo cual no es más, que la velocidad “ů”; por lo tanto:

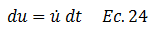
Teniendo claro estas acotaciones, comencemos con el abordaje matemático de la ecuación diferencial desde un enfoque energético. Seleccionemos en primera instancia el componente asociado a la fuerza de amortiguamiento “fd”:

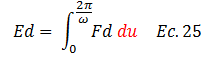
Sustituimos la ecuación N°24 en la N°25:

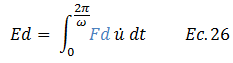
Adicionalmente, al chequear la ecuación diferencial de equilibrio dinámico, y el esquema conceptual de la imagen N°05, nos damos cuenta que “fd” es el producto de la velocidad “ů” por la constante de amortiguamiento “c”. En este sentido la ecuación N°26 se rescribe así:

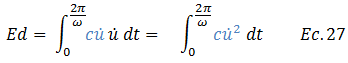
Dado que se conoce la solución particular en términos de desplazamiento, procedemos a obtener su primera derivada con respecto al tiempo, para así poder sustituir en la ecuación N°27. Se tiene en consideración en este proceso de derivación que “uo”, es una constante:

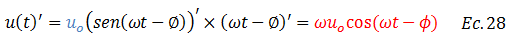
Sustituimos el término resaltado en color “rojo” en la ecuación N°27:

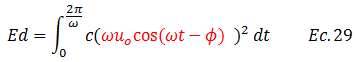
Eliminamos paréntesis:

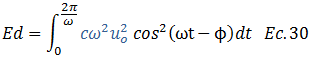
Los términos resaltados en color “azul” en la ecuación N°30 son constantes, por lo que podemos extraerlos de la siguiente forma:

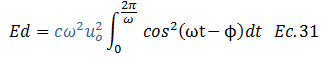
La solución de esta integral definida se ilustra en el siguiente esquema conceptual:

Imagen N°06: solución de la integran definida representada por la ecuación N°31

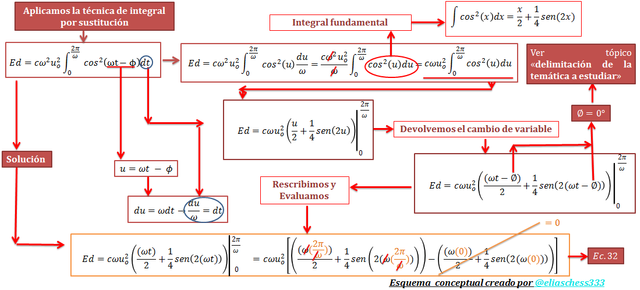
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.

La solución dada por la ecuación N°32, la podemos rescribirla de la siguiente manera:

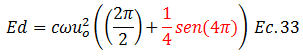
El término resaltado en color “rojo” es cero, por lo que la ecuación N°33 queda de la siguiente forma:

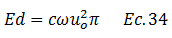
Conociendo la expresión de fracción de amortiguamiento crítico “ξ”:

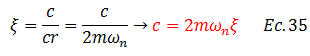
Sustituimos la ecuación N°35 en la N°34:

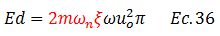
Por su parte:

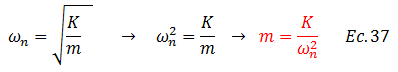
Procedemos a sustituir la ecuación N°37 en la N°36:

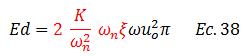
Rescribiendo la ecuación N°38, finalmente tenemos para la energía disipada por el amortiguador viscoso “Ed” la siguiente expresión:

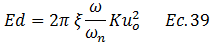
Al analizar la ecuación N°39, podemos concluir que la energía disipada por el amortiguador viscoso no es constante en el tiempo, y estará influenciada directamente por la frecuencia de la excitación externa “ω”, pudiéndose hablar de una relación directa proporcional, es decir, si “ω” aumenta, eso ocurrirá también para “Ed”. Esta es una ecuación de mucha importancia, dado que las ideas que se desprenden nos servirán de base para aplicaciones más avanzadas, donde el sismo sea la excitación de interés. Adicionalmente es importante acotar que dicha ecuación es una forma cualitativa para ver las variables que inciden en el proceso disipación de energía de un sistema estructural sometido a una vibración armónica y que se comporta elásticamente, y no ha de usarse para obtener una información cuantitativa, para tal fin utilizaremos la herramienta computacional NONLIN V 7.14, lo cual constituye la parte dos de este trabajo.

Ahora bien, continuando con el abordaje energético de la ecuación diferencial de equilibrio dinámico, es interesante reflexionar sobre la energía de entrada al sistema “Ei” a causa de la excitación externa. Para ello, planteemos la siguiente interrogante, la cual te despertará una cierta curiosidad amigo lector:

Sí en un sistema que se comporta elásticamente el amortiguador viscoso es el encargado de disipar energía de entrada ¿significa que la expresión de energía de la ecuación N°39 es la misma para “Ei”?

Te invito a que nos sigamos deleitando con las aplicaciones de las matemáticas en la dinámica estructural, para dar respuesta a esta interrogante. Basados en los principios de trabajo y energía (ver Ec.22) y en el tratamiento matemático desarrollado en las ecuaciones N°23, N°24 y N°28; surge el siguiente reto a superar:

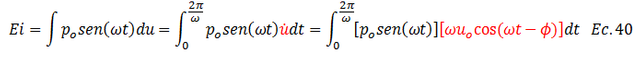
Esta ecuación se puede rescribir a la forma:

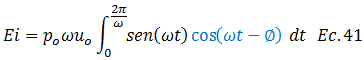
El término resaltado en color “azul” de la ecuación N°41, puede ser tratado con la ayuda de la siguiente identidad trigonométrica:

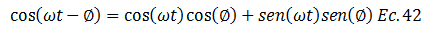
En este sentido la ecuación N°41 queda de la siguiente forma:

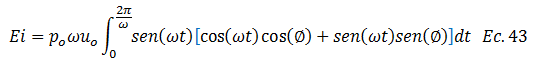
Aplicamos distributiva y planteamos la suma algebraica de integrales:

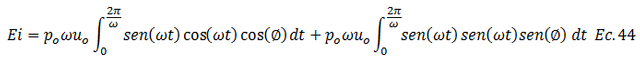
Rescribimos las integrales resultantes y procedemos a su respectiva solución, hecho que se ilustra didácticamente en la imagen N°07:

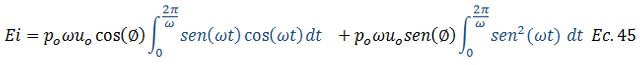
Imagen N°07: solucionando las integrales de la ecuación N°45

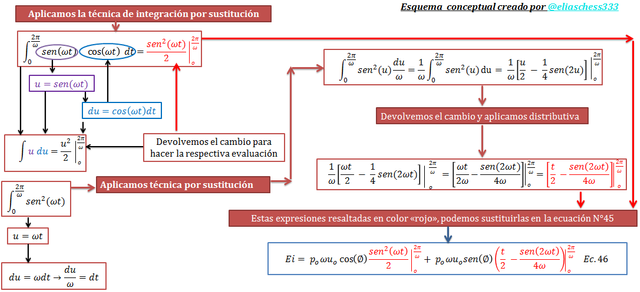
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.

Realizamos la evaluación de la ecuación N°46, la cual previamente requiere un tratamiento matemático; este proceso se ilustra a continuación:

Imagen N°08: evaluando la integral definida para la energía de entrada “Ei

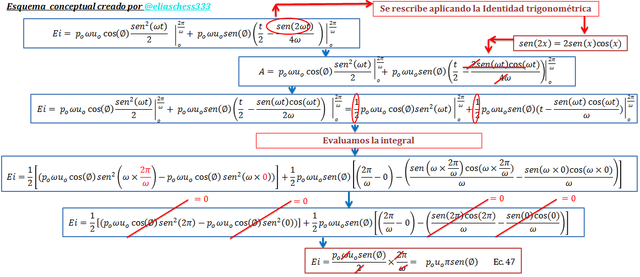
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.

Esta expresión a la que se ha llegado puede ser rescrita tratando el término “senϕ”, basándonos en la trigonometría desarrollada en la imagen N°03 y acotando que consideraremos los catetos en términos absolutos. En este orden de ideas, tenemos que el ángulo de fase “ϕ” viene dado por:

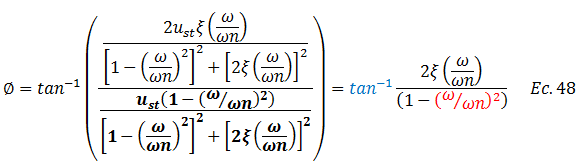
Para el caso en estudio, donde la frecuencia natural “ωn” es mayor que la frecuencia de la excitación externa “ω,” el cociente que resulta de dividir los catetos es un valor tan pequeño que abre la puerta a la teoría de ángulos infinitesimales, hecho que permite que en la ecuación N°48 el término resaltado en color “azul” sea simplificado, es decir:

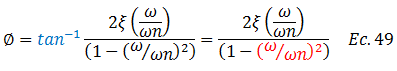
Además el término resaltado en color “rojo” de la nueva expresión, por la misma situación en lo referente a los valores que toman las frecuencias involucradas, donde asumimos que la fuerza varía lentamente (ver tópico “DELIMITACIÓN DE LA TEMÁTICA A ESTUDIAR”), tiende a un valor muy pequeño, lo que significa que la resta que se da en el denominador se puede aproximar a la unidad, obteniendo:

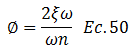
Al mismo tiempo, por tratarse de ángulos infinitesimales (tendientes a cero para el caso en estudio), permite el siguiente planteamiento:

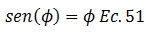
En este orden de ideas, la ecuación N°47 (ver imagen N°08) la podemos expresar así:

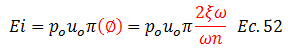
Partiendo del hecho de que la deformación máxima dinámica “uo” tiende a ser igual a la deformación máxima estática “ust”, por la condición de que la fuerza varía lentamente (ver tópico “DELIMITACIÓN DE LA TEMÁTICA A ESTUDIAR”), podemos plantear lo siguiente:

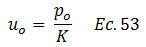
Entonces:

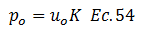
Sustituimos la ecuación N°54 en la N°52:

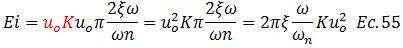
Luego de este tratamiento matemático, y de haber demostrado que la energía de entrada “Ei” coincide con la energía de amortiguamiento “Ed”, esto nos lleva a pensar que la energía representada por los otros términos de la ecuación N°01, referentes a la energía potencial “Es” y a la energía cinética “Ek”, no experimentan cambios en el tiempo que dura la excitación armónica. Esto puede ser demostrado perfectamente desde el enfoque energético, en conjunto con los aportes del cálculo integral; lo cual se ilustra didácticamente en los esquemas conceptuales de las imágenes N°09 y N°10.

Imagen N°09: tratamiento matemático de la energía potencial

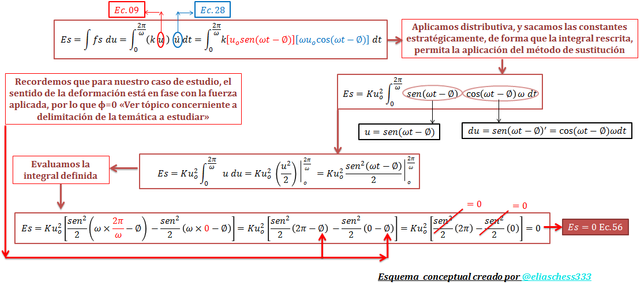
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.

Para el caso del abordaje de la energía cinética, resulta necesario obtener la segunda derivada de la función desplazamiento en el tiempo “u(t)”, lo cual se hace derivando la ecuación N°28, que hace referencia a “ů”:

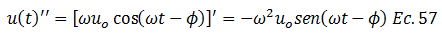
Ahora si estamos preparados para hacer el abordaje energético de la energía cinética:

Imagen N°10: tratamiento matemático de la energía cinética

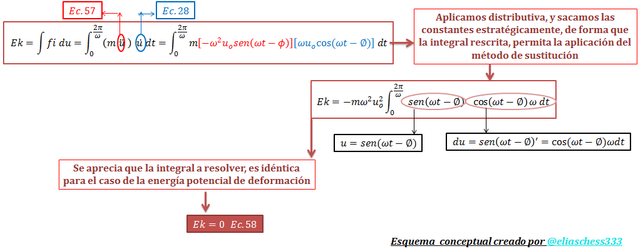
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint.

La interpretación de los resultados obtenidos tanto para la energía potencial “Es” como para la energía cinética “Ek”, indica que en los ciclos de vibración que se desarrollan, estas energías no experimentan variación. Algo similar a lo que ocurre en los sistemas conservativos (sin presencia de amortiguamiento), sujetos a un régimen de vibración libre.

CONCLUSIONES

Es de mucha importancia en nuestra formación como ingenieros sismoresistentes, el estudio de sistemas estructurales sometidos a una vibración forzada armónica, por el hecho de que sirve de entrenamiento para ir comprendiendo conceptos de la dinámica estructural, de gran utilidad cuando sea la excitación sísmica la que provee la energía de entrada al sistema. Entre las conclusiones de mayor importancia que se derivan del presente trabajo, tenemos las siguientes:

1.- En un sistema con amortiguamiento viscoso “c” sometido a una vibración forzada armónica, la energía disipada asociada a este componente “Ed”, variará conforme aumenta o disminuye la frecuencia de la excitación externa “ω”.

2.- Si la respuesta de la estructura en el rango de comportamiento elástico está gobernada por grandes deformaciones, es evidente de acuerdo a la ecuación N°39 que esto influye en los valores de “Ed”; pero el hecho de grandes deformaciones, está también íntimamente ligado con “ω”, tal como se reseñó en la primera conclusión.

3.- En un sistema estructural que se comporta elásticamente, el proceso de disipación de la energía de entrada “Ei” no implica la presencia de daño (comportamiento plástico), puesto que es en el amortiguador viscoso donde recae la responsabilidad de disipar toda la energía que entra al sistema; lo cual se demostró en el tratamiento matemático realizado para “Ei”, donde nos dimos cuenta que esta coincide con el valor de Ed”.

4.- Toda deformación y movimiento relativo de la masa con respecto a la base, implica una acumulación de energía potencial “Es” y energía cinética “Ek”; las cuales en los sistemas conservativos (aquellos que no disipan energía), coincide con la energía de entrada “Ei”.

5.- En el caso de los sistemas que no conservan energía, producto de la presencia del amortiguador viscoso “c”, la variación en el tiempo que dura la excitación externa para “Ek” y “Es” es nula; lo cual se demostró en las ecuaciones N°56 y N°58.

En la parte dos de este trabajo, profundizaremos con ayuda de la herramienta computacional NONLIN V 7.14, en cada una de estas conclusiones presentadas. Fue todo un honor escribir para ustedes:

@eliaschess333

FUENTES DE INFORMACIÓN CONSULTADAS

01.- GIECK K.Y GIECK R. 2003. ALFAOMEGA GRUPO EDITOR.

02.- CHOPRA ANIL K. 2014. DINÁMICA DE ESTRUCTURAS. CUARTA EDICIÓN. PEARSON EDUCACIÓN, MÉXICO.

03.- FIERRO E. Y GARCÍA E.2005. SEMINARIO DE INGENIERÍA SÍSMICA. PONTIFICIA UNIVERSIDAD CATÓLICA MADRE Y MAESTRA. REPÚBLICA DOMINICANA.

LECTURAS RECOMENDADAS

04.- SANTANA E. 2018. DETERMINACIÓN EXPERIMENTAL DEL AMORTIGUAMIENTO EN ESTRUCTURAS. UN ENFOQUE MATEMÁTICO CON APLICACIONES EN LA INGENIERÍA SISMORESISTENTE. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/determinacion-experimental-del-amortiguamiento-en-estructuras-un-enfoque-matematico-con-aplicaciones-en-la-ingenieria

05.- SANTANA E. 2018. ABORDAJE DIDÁCTICO DEL CONCEPTO DE RESONANCIA A TRAVÉS DE UN ENFOQUE MATEMÁTICO Y SUS APLICACIONES EN LA DINÁMICA DE ESTRUCTURAS. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/abordaje-didactico-del-concepto-de-resonancia-a-traves-de-un-enfoque-matematico-y-sus-aplicaciones-en-la-dinamica-de-estructuras

06.- SANTANA E. 2018. ESTUDIO DE LA INFLUENCIA DEL AMORTIGUAMIENTO EN LA RESPUESTA DINÁMICA MÁXIMA DE UN SISTEMA ESTRUCTURAL DE UN GRADO DE LIBERTAD SOMETIDO A UNA VIBRACIÓN FORZADA ARMÓNICA. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/estudio-de-la-influencia-del-amortiguamiento-en-la-respuesta-dinamica-maxima-de-un-sistema-estructural-de-un-grado-de-libertad

07.- SANTANA E. 2018. COMPRENDIENDO LAS APLICACIONES DE LAS MATEMÁTICAS EN LA ESTIMACIÓN DEL PERIODO Y FRECUENCIA NATURAL DE UN PORTICO PLANO. CASO: SISTEMA DE UN GRADO DE LIBERTAD. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/comprendiendo-las-aplicaciones-de-las-matematicas-en-la-estimacion-del-periodo-y-frecuencia-natural-de-un-portico-plano-caso