Series and Discrete Fourier Transforms (Applications)
Hello friends of Steemit!
In the articles Fourier Series and Transforms (APPLICATIONS) part 1 and Fourier Series and Transforms (APPLICATIONS) part 2 , the Fourier series and the Fourier transform of continuous time signals (TC) were defined, which are functions that are defined for all "t" (time).
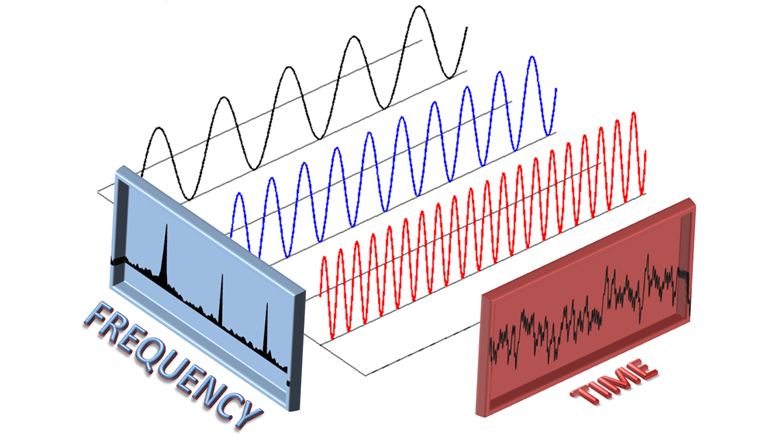
In this publication I present the Fourier mathematical treatment for discrete type signals.
Discrete signals are functions that are only defined for certain time values, that is, for a set of discrete values.
Discrete signals are of great importance in the analysis of a great variety of systems in which their temporal behavior is inherently discrete.
Sequential state machines (computers), demographic studies, stock market indexes, are some of the examples in which we find signals with discrete attributes.
The current digital processors, which provide great benefits due to their processing speed and calculation capacity, are systems in which discrete-type sequences are used.
Discrete signals are denoted by the form "x [n] ", where "n" is the independent variable of time defined only for integer values.
Fourier Series in Discrete Time of a periodic x [n] sequence (DTFS):
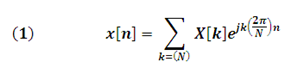
k = 0,1,2,3,……N-1
N ➞ Fundamental Period of x[n]
"X[k]" Represents the discrete Fourier coefficients and are defined in the form
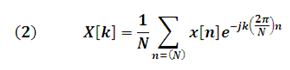
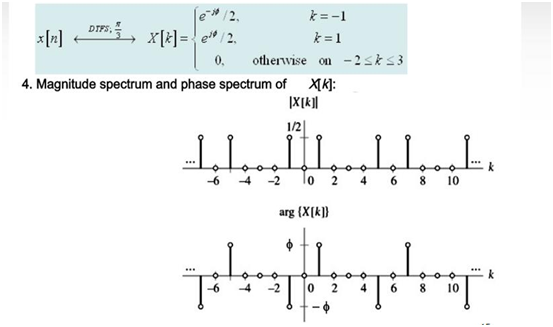
The Fourier coefficients allow determining the spectral behavior (in frequency) of x [n]. These coefficients allow the construction of the magnitude and phase spectra. (See figure 1)
Edited image
Fourier Transform in Discrete Time of a non-periodic sequence of values x[n] (DTFT):
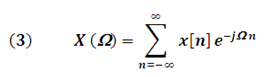
Ω ➞ frequency in discrete time
Symbolically, the fourier transform of a signal x[n] is denoted by the form:
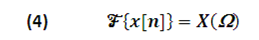
For the discrete time fourier transform of a signal x[n] to exist, must satisfy the condition:
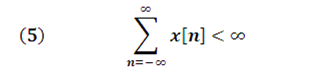
Discrete Time Fourier Inverse Transform
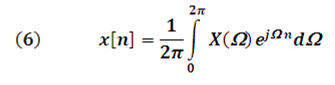
Symbolically it is written:
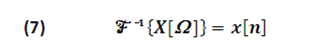
Because the Fourier Transform X(Ω ) is a complex signal, it can be written as:
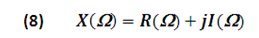
Where:
R(Ω) is the Real part
I(Ω) is the imaginary part
Applying the Euler Formula to equation (3) you get:
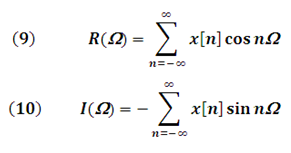
In polar coordinates can be expressed as:
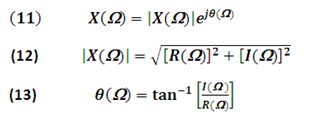
Equations (12) and (13) allow obtaining the magnitude and phase spectra of the discrete signal, as shown in the following example.
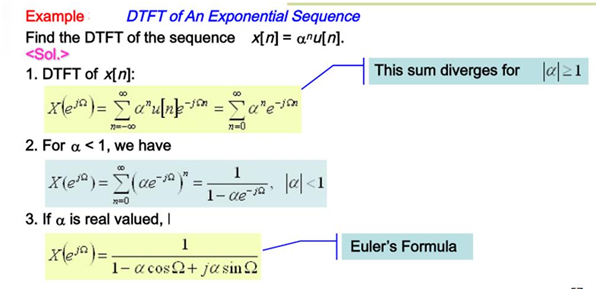
Edited image

Edited image
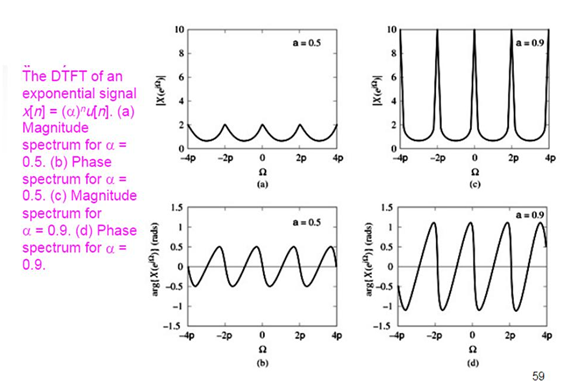
Edited image
APPLICATIONS
The following images show one of the medical applications of fourier spectra, obtained in the monitoring of the heartbeat of an individual with normal beats and another with ventricular tachycardia.
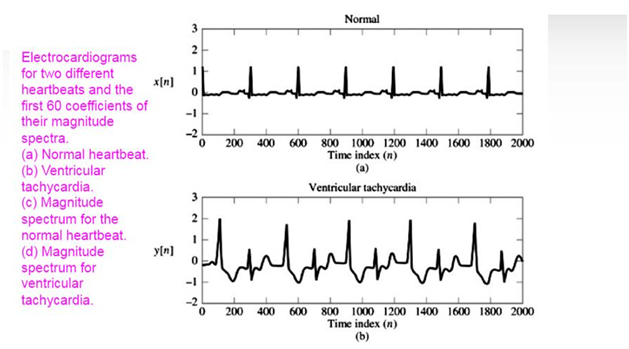
Edited image
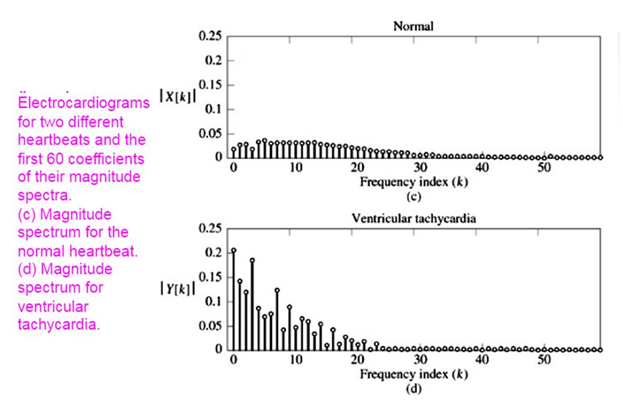
Edited image
References
Introduction to communication systems / Ferrel G. Stremler.-2ed.
Digital Signal Processing Using MATLAB. Vinay K. Ingle, John G. Proakis. Third Edition.
Differential Equations with Boundary-Value Problems, 6th Edition / Edition 6.
http://lcr.uns.edu.ar/fvc/NotasDeAplicacion/FVC-Martin%20Carrizo.pdf