Fourier Series and Transforms (APPLICATIONS) part 2

Hello friends of Steemit!

In the previous article we saw how to obtain the Fourier series of a periodic signal in continuous time, which leads to discrete spectra of magnitude and phase, essential in the analysis of the frequency behavior of a signal.

Since in practice most of the signals are non-periodic, it is necessary to generalize the Fourier series for the frequency analysis of this type of signals.

Source

The Fourier transform allows to determine the frequency behavior of any signal and is given by:

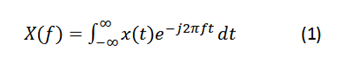
Symbolically, the fourier transform of a signal x(t) is denoted by the form:

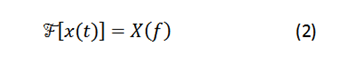
For the Fourier transform of a signal to exist, it must satisfy the condition:

Because the Fourier transform X(f) is a complex signal, it can be written as:

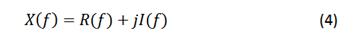
Where:

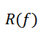is the Real part
is the imaginary part

In polar coordinates can be expressed as:

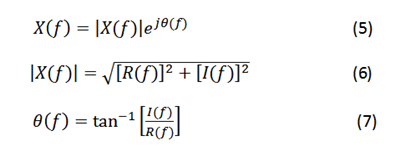
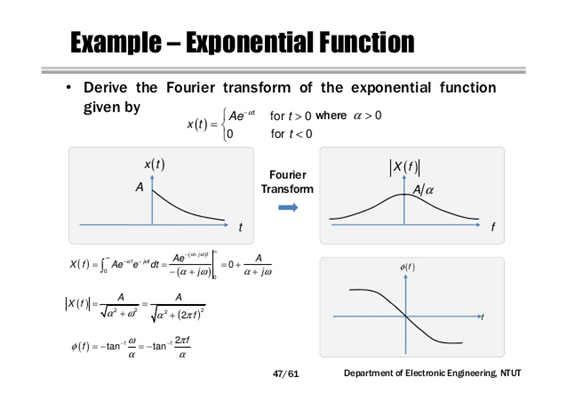
Equations (6) and (7) allow the construction of the continuous Magnitude and Phase Spectra as illustrated in the following example.

Source

In the case of signals in the Frequency domain, the inverse Fourier transform is used, which allows expressing the signal in the time domain. This inverse transformation is given by the equation:

Symbolically it is written

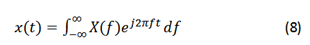
The functions x(t) and X(f) form a transformed pair which indicates a transformed in two directions and is denoted as:

The following table shows the most common transformed pairs obtained from equation (1).

Source

APPLICATIONS

The fourier transform has been very useful in different areas of Physics and Engineering.
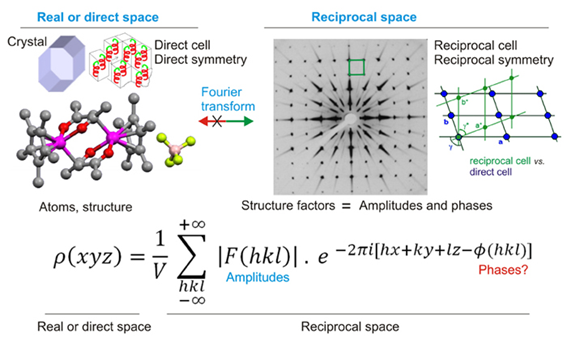
In 1915 W.H Bragg used the Fourier transforms in his studies of X-ray diffraction.

In the following image it is observed that it is possible to move from a direct space described by the electronic density of a crystalline structure "ρ(x, y, z)" to a reciprocal space which shows the diffraction pattern.

The integers l, k and h are the Miller indices that describe the faces (planes) of the crystal structure.

Source

In the process of image analysis using the proton nuclear magnetic resonance (NMR) method, the Fourier transform is also a valuable tool in the task of spectral analysis of samples.

Source

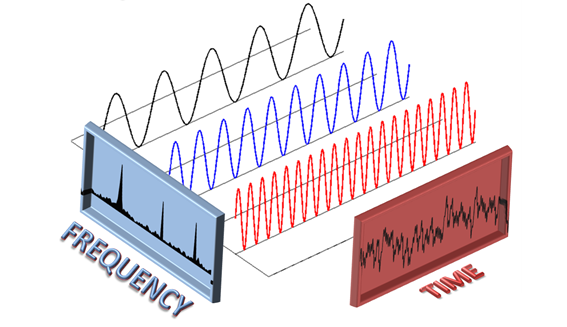
Frequency is the main parameter in data processing and systems analysis. The bandwidth of a system is the range of frequencies in which the maximum amplitudes and power of a signal are contained, the filters are also characterized by this parameter.

For this reason, the Fourier transform offers a wide variety of applications by allowing the conversion of a time domain signal to the frequency domain without this implying or resulting in loss of information.

References:

• Introducción a la Cristalografía. Donald E. Sands. Editorial Reverte. S.A.

• Introduction to communication systems / Ferrel G. Stremler.-2ed.

• Digital Signal Processing Using MATLAB. Vinay K. Ingle, John G. Proakis. Third Edition.

• Differential Equations with Boundary-Value Problems, 6th Edition / Edition 6.

• https://es.wikipedia.org/wiki/Espectrofot%C3%B3metro_de_transformada_de_Fourier.

• http://www.xtal.iqfr.csic.es/Cristalografia/parte_05_6.html.

• https://es.wikipedia.org/wiki/Serie_de_Fourier