Calcular el perímetro de un cuadrado, inscrito en la dimensión de un círculo de radio conocido, a partir de un producto notable.

in #steemstem • 6 years ago (edited)
Un cordial saludo a toda la comunidad de steemit, en especial a las comunidades de #stem-espanol y #steemstem; el siguiente post, se basara, como podemos calcular el perímetro de un cuadrado, inscrito en la dimensión de un círculo de radio conocido, a partir de un producto notable. Ya que el producto notable, se refiere a productos, que deben sobresalir, de la generalidad, con el propósito de agilizar operaciones, al no realizarlas según su principio.

1.png

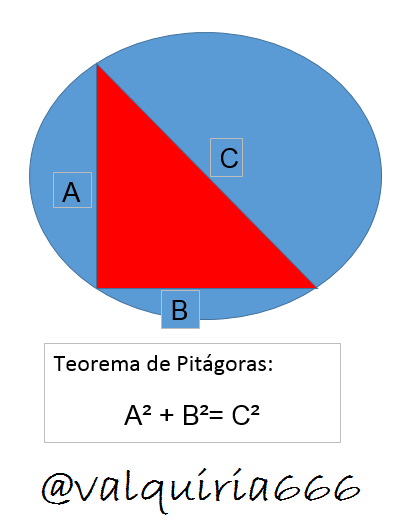
Figura 1; autor:@valquiria666.


En el proceso del desarrollo de todos los binomios siempre aparece una expresión que se identificar por un producto notable.


Se sabe para calcular el perímetro es simplemente cuatro veces la longitud del lado:


P=4L.


En este caso tenemos la siguiente información:


Para (x=2); el lado C = (2X+1); en dónde: A=B=L=?


Aplicamos el teorema de Pitágoras, para calcular L, como podemos observar en la figura 1 tenemos un triángulo rectángulo con lados a y b y una hipotenusa c; en donde se conoce el valor de c; a y b tiene el mismos valor.

A² = (2X+1) ²
A² = 4X²+4X+1
A² = 4(2) ²+4(2)+1
A² = 16 + 8 + 1
A² =25
A= √25
A= 5

2.png
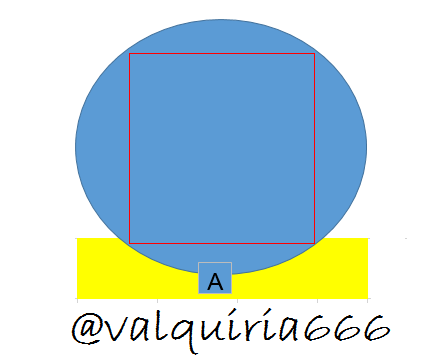
Figura 2 autor:@valquiria666.

Perímetro:
P= 4*5= 20
P= 20.
La longitud del lado A para el cuadrado inscrito = √25 = 5.

Concluyo con lo siguiente; es importante el racionamiento lógico analítico, como fundamento matemático, para aplicación tanto en la vida cotidiana o inconveniente, que experimenta otras ciencia, para fundamentar sus teoremas. ya que, gracia a ello de tener habilidad de pensar y trabajar en términos de números generando, la capacidad de razonamiento lógico, nos sirve de base de enseñanza, para saber hasta donde podemos llegar, tanto en el ámbito escolar o académico como fuera de él, y favorece al desarrollo de la cultura y a nuestra sociedad en ver la realidad de las cosas.

Fuente para este post:

Algebra y trigonometría con geometría analítica - Página 21
Arthur Goodman, ?Lewis Hirsch 1996.

Algebraic Geometry
por Robin Hartshorne

Producto notable

pies de articulo valquiria_j.jpg

#stem-espanol #edu-venezuela #cervantes #proconocimiento
6 years ago in #steemstem by
$0.03
  • Past Payouts $0.03
  • - Author $0.02
  • - Curators $0.00
13 votes
Reply 4
Sort:  
  • Trending
    • [-]
     6 years ago 

    gracias por tu aporte es muy practico @valquieria666

    $0.00
      Reply
      [-]
       6 years ago 

      gracias por compartir tu caso practico y educativo @valquiria666

      $0.00
        Reply
        [-]
         6 years ago 

        Congratulations @valquiria666! You have completed some achievement on Steemit and have been rewarded with new badge(s) :

        Award for the number of upvotes

        Click on the badge to view your Board of Honor.
        If you no longer want to receive notifications, reply to this comment with the word STOP

        Do not miss the last post from @steemitboard!

        Participate in the SteemitBoard World Cup Contest!
        Collect World Cup badges and win free SBD
        Support the Gold Sponsors of the contest: @good-karma and @lukestokes

        Do you like SteemitBoard's project? Then Vote for its witness and get one more award!

        $0.00
          Reply

          Coin Marketplace

          STEEM 0.26
          TRX 0.20
          JST 0.038
          BTC 95956.24
          ETH 3566.05
          USDT 1.00
          SBD 3.78