A medida que los avances en la física y la ciencia se fueron cuajando desde el tiempo antiguo hasta el presente, se gestaron las bases de lo que hoy en día se conoce como cálculo infinitesimal. Todo lo relacionado con esta herramienta innovadora (cálculo) ha hecho que a medida que la ingeniería, ciencia, tecnología, medicina y todos los avances que el hombre contemporáneo ha logrado sigan creciendo, por lo que existe una exigencia en aprender cálculo como una de las principales bondades del mundo contemporáneo.

^{Fuente de imagen. Pixabay}

Cuando me refiero a que aprender cálculo es solo uno de sus multas, es porque dentro de los objetivos más importantes está en utilizar todo ese conocimiento sobre cálculo diferencial e integral para modelar y diseñar sobre nuevas herramientas matemáticas que resuelvan problemas de la vida real, y como un objetivo terciario diría yo que también podría ser trazar la meta que este aprendizaje nos llevará a la resolución de problemas reales y cotidianos de nuestro comienzo más sencillo.

Para el aprendizaje del cálculo, es necesario transformar y traducir todo ese conjunto de axiomas, teoremas y demostraciones de muchos de los complejos y difíciles enunciados que nos dejarán a los padres del cálculo infinitesimal (Isaac Newton y Leibniz) en herramientas fáciles de comprender y aplicar . Realmente representa una tarea algo difícil de calcular la poca recepción que se experimenta en las personas para aprender cálculo.

Debido a esta complejidad para enseñar cálculo, complejidad una serie de estrategias producto de la experiencia en la interacción con los alumnos del ciclo universitario, entre las que puedo identificar y explicar:

[1] En la mayoría de los casos las preguntas y ejercicios prácticos que se realizan van enmascarados dentro de los parámetros complejos de la misma esencia del cálculo, por lo que se recomienda el alumno se cerciore de entender muy bien la pregunta o el ejercicio que se pueden, por lo que es muy importante, incluso que se pueden hacer preguntas de autoanálisis como:

- ¿Cuáles son los datos?

- ¿Qué es concretamente lo que se pide encontrar?

^{Fuente de imagen. Pixabay}

[2] En la disertación y el entendimiento de las preguntas o ejercicios planteados, es muy importante que puedas contar con un plan esquematizado, como algo previo al desarrollo del ejercicio, para este plan se puede concebir como planos estratégicos enfocados en esquemas, desde siempre de lo más sencillo a lo más complejo, por nada del mundo es recomendable empezar desde lo más complejo a lo más fácil, y en general tener la mano cualquier recurso que creamos nos puede ayudar a la comprensión y resolución de los problemas, entre estos recursos pueden ser un formulario, esquematizar diagramas, utilizar recursos tecnológicos como calculadoras científicas, entre otros, todo control de sus necesidades y comprensión.

^{Fuente de imagen. Pixabay}

[3] La correcta ejecución del plan nos permite ejecutar las instrucciones de respuesta de todas las preguntas, por lo que la ejecución del plan debe contener la capacidad del aprendizaje en poder traducir las respuestas numéricas en palabras, un ejemplo de los que les hablo es :

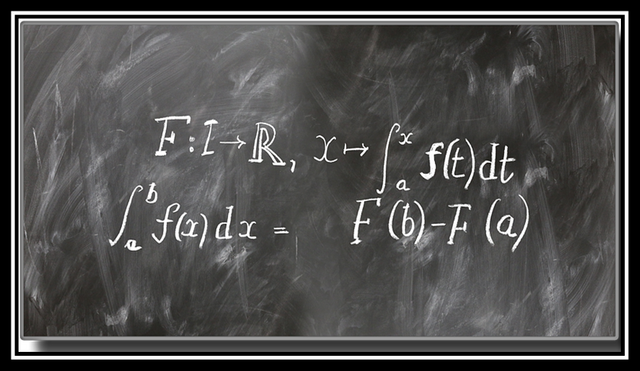
Supongamos que resolvemos una integral para el cálculo del área bajo la curva y nos da un resultado de X = 8,5. Lo recomendable sería traducir esta respuesta en palabras que satisfagan el entendimiento del ejercicio, por ejemplo, podría escribir en sinónimo como: "el área bajo la curva de la zona marcada en el gráfico es aproximadamente 8,5 unidades cuadradas".

[4] No podemos conformarnos con simplemente dar una respuesta, es necesario que podamos evaluar y analizar si la respuesta que estamos dando resulta coherente en la base de la demanda del ejercicio planteado, ya que la respuesta de demostración que demuestra que existe la posibilidad de que esa respuesta se puede contrastar o no.

Estas cuatro estrategias no significan el abecedario inmediato para el aprendizaje del cálculo, pero si es el resultado y análisis de algunos años de trabajo en consecuencia al rendimiento estudiantil a nivel universitario, los triunfos y fracasos en la interacción con el alumno me han llevado a trabajar sobre los asuntos nombrados en las estrategias nombradas previamente, sin embargo cada quien pueda desarrollar sus estrategias en base al rendimiento y circunstancias de su grupo de alumnos.Mientras más se trabaje en los estímulos del aprendizaje del cálculo se puede romper mameluco con las barreras difíciles para que las personas puedan entender el miedo que existe para aprender cálculo simplemente es un conjunto de enigmas negativos para detener el desarrollo del aprendizaje de esta noble ciencia auxiliar de la matemática.

Cuando realizamos una mirada previa al cálculo, pueden variar quirúrgicamente diversas interrogantes entre las que están:

¿Qué es el cálculo?

Quizá muchas personas cuando están aprendiendo cálculo se les hace un poco difícil su aprendizaje, ya que en muchas ocasiones los docentes que explicamos cálculos nos vamos directamente a desarrollar y explicar el contenido que envuelve esta disciplina, sin embargo cuando toda esa persona que quiera aprender Cálculo se inicia en un aprendizaje partiendo de los más básicos, es entonces el momento donde le surge el interrogante más sencillo que se puede hacer todo aquel principio principio principio principio principio principiante: ¿Qué es cálculo?

Para responder a esta pregunta es necesaria buscar los orígenes del cálculo, analizar bajo qué circunstancia nace esta disciplina, y qué necesita vino a suplir una razón de los problemas que identifica otras disciplinas, tal es el caso de la física. Es por eso que cuando se analiza estos orígenes y nos damos cuenta de que existen problemas para dar respuestas a aquellos síntomas que involucran cambios, tal es el caso de la velocidad y la aceleración, pero incluso este caso de estudio (cálculo) pudo evolucionar y dar respuesta más concretas a otros fenómenos que involucran cambios muy dinámicos, ante el análisis de estos antecedentes podemos decir que el cálculo es la matemática de los cambios, y cuando hago referencia a los cambios no me refiero exclusivamente a la velocidad y la aceleración,

Al hablar del cálculo como la matemática de los cambios, podemos extrapolar su estudio y aplicación a los siguientes elementos:

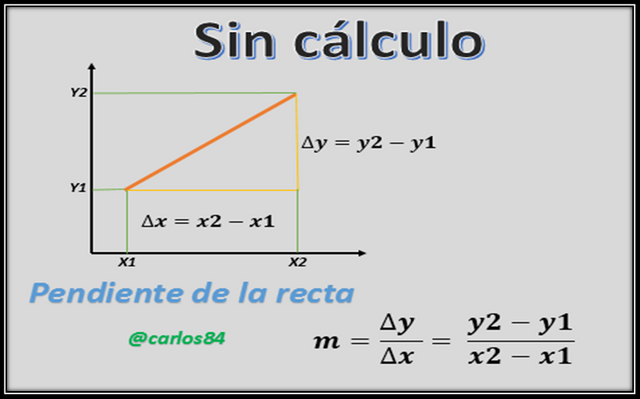
- Cálculo de pendientes de rectas tangentes (sobre todo aplicable cuando se conoce un solo punto).

-Cálculo de áreas y volúmenes.

-Cálculo de centros de masas y momentos de inercia.

Lo más importante de entender el concepto de cálculo no solo es su alcance de aplicación, sino entender qué gracias a esta disciplina y las ideas innovadoras de sus precursores han permitido que científicos, ingenieros, economistas y hasta expertos en humanismo hayan logrado modelos matemáticos adaptados a las necesidades de cada una de las ramas a las cuales son especialistas. Muchos de estos modelos matemáticos son a partir de los principios básicos del cálculo que en muchas de las ocasiones vienen a dar respuestas a situaciones de la vida real.

Se podría pensar que las matemáticas tradicionales también tratarán sobre cálculo de velocidades, aceleraciones, pendiente de rectas, entre otros aspectos más, sin embargo se puede encontrar una diferencia notable entre las matemáticas previas al cálculo (matemática tradicional) y el cálculo infinitesimal, esta diferencia está marcada en la forma que está involucrada las matemáticas previas al cálculo con los elementos nombrados previamente son de forma estática, mientras que el cálculo es más dinámico, para dar cierto sentido de credibilidad a lo que me refiero quiero citar los siguientes ejemplos:

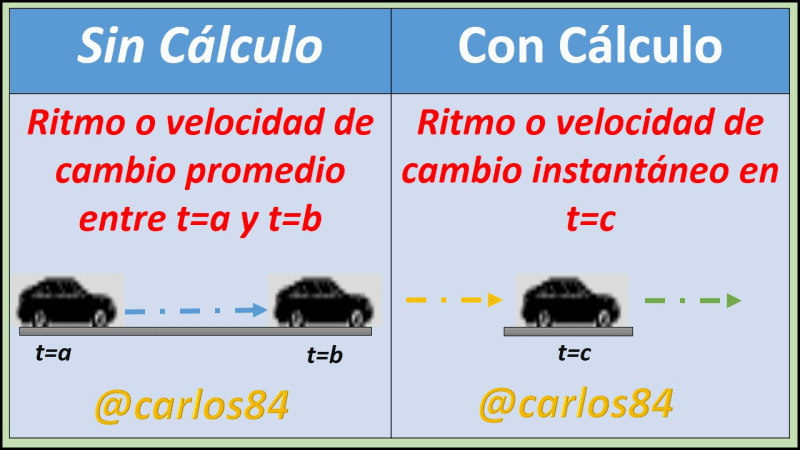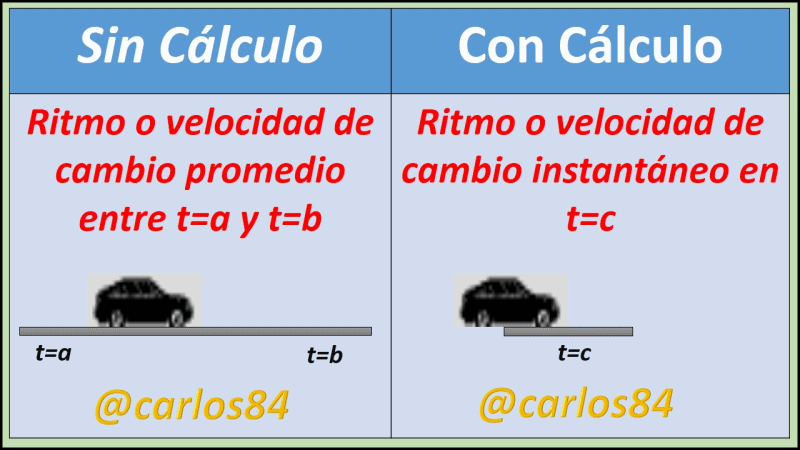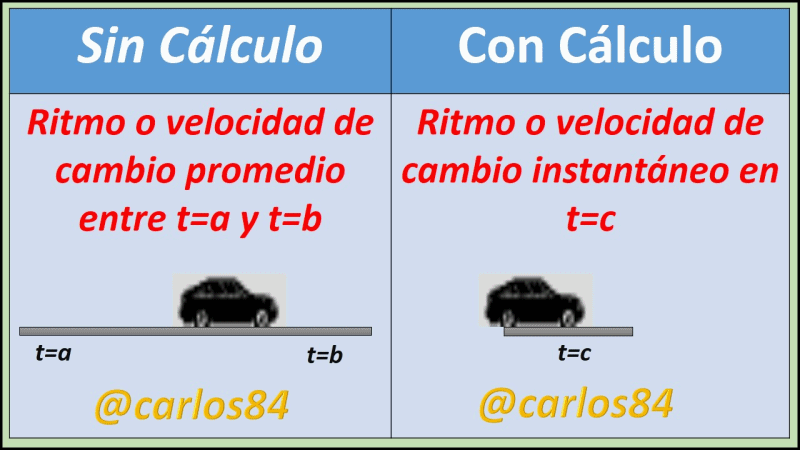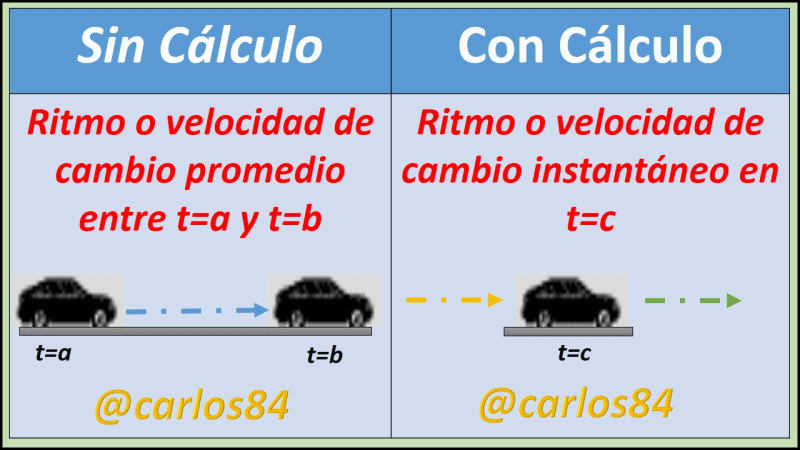
[1] Con las matemáticas previas al cálculo se puede llegar a analizar el movimiento de un objeto que se mueva con velocidad constante de un punto A hasta un punto B. Sin embargo con las herramientas y los conocimientos que se tienen del cálculo se puede llegar calcular la velocidad de un móvil que se mueve con la velocidad variada (y decir que puede llegar a calcular la velocidad del móvil en un punto dado de la trayectoria (velocidad instantánea).

^{Autor de la imagen @ carlos84}

[2] Las matemáticas previas al cálculo calcular los valores de la pendiente de una recta, pero cuando se calcula la pendiente de una curva en un punto es necesario el cálculo, para entender esto es recomendable observar la siguiente imagen:

^{Autor de la imagen @ carlos84}

El cálculo de la pendiente de la recta en el caso de la física en la parte de la cinemática, suele ser muy importante para calcular la velocidad promedio de un móvil que se desplaza en línea recta entre el punto inicial de partida y un punto final, sin embargo la interrogante surge cuando deseamos calcular la velocidad en un instante específico de tiempo, para ello es necesario el cálculo diferencial, en la imagen animada que muestra la continuación se demuestra que es una razón de la necesidad de calcular la pendiente de la recta tangente a un punto de la curva es que se descubre la derivada:

^{Autor de la imagen @ carlos84}

[3] En la antigüedad se estudiaba sin ningún problema el análisis de todo lo relacionado a la recta tangente a un círculo, sin embargo no era sino hasta las bases del cálculo que se pudo estudiar y analizar la pendiente de una curva tal y como se vio previamente en la figura animada.

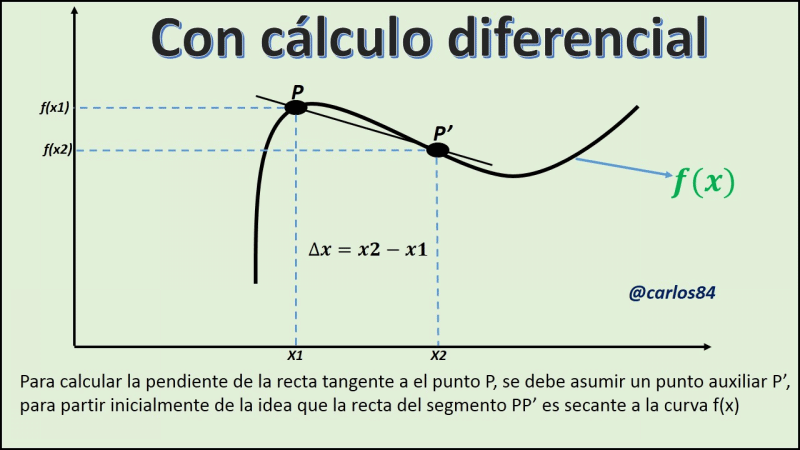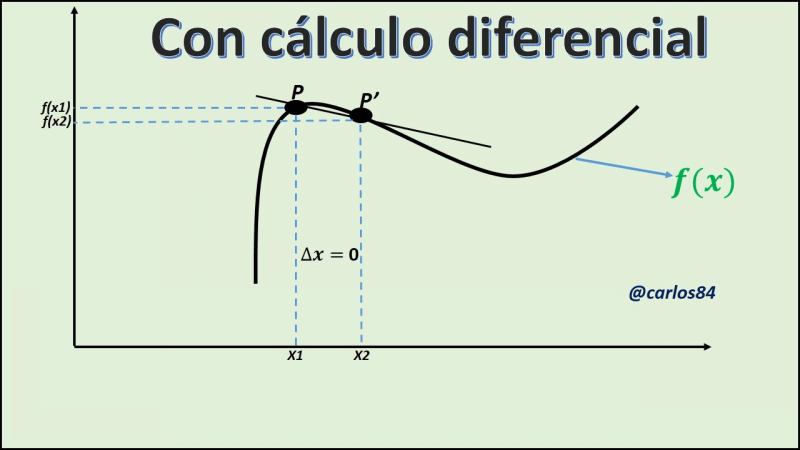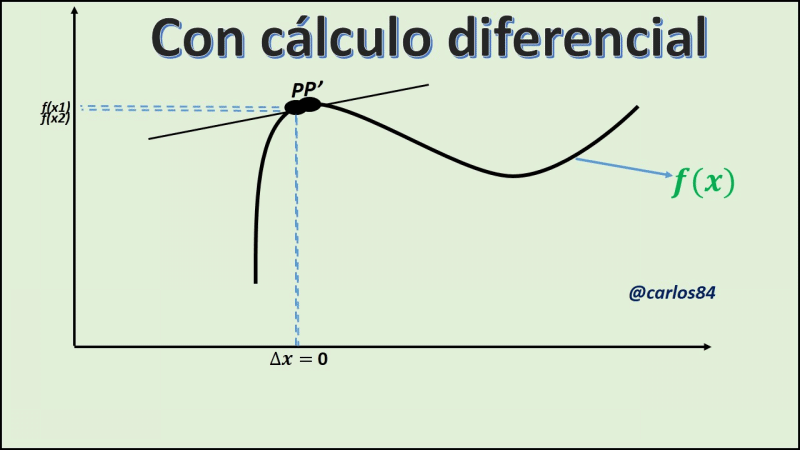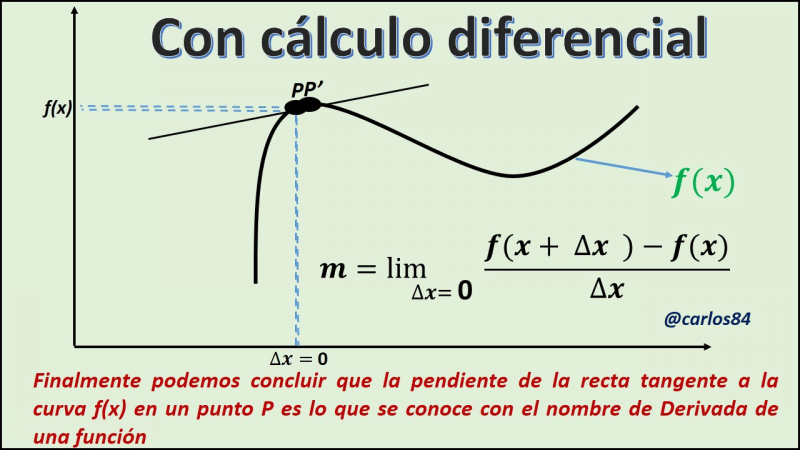
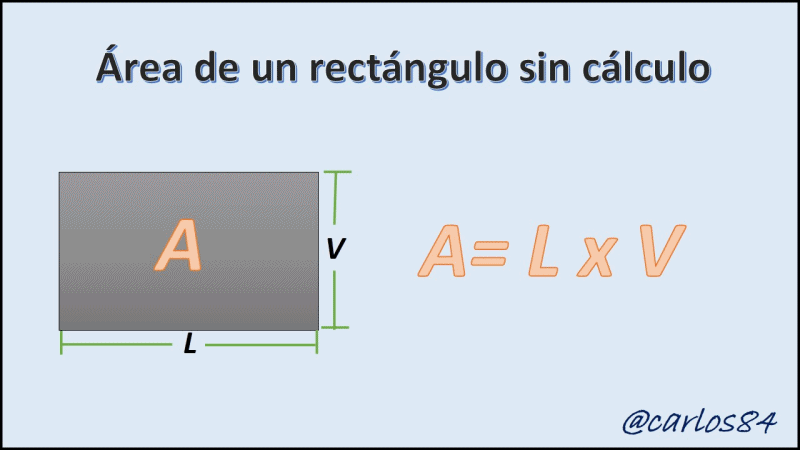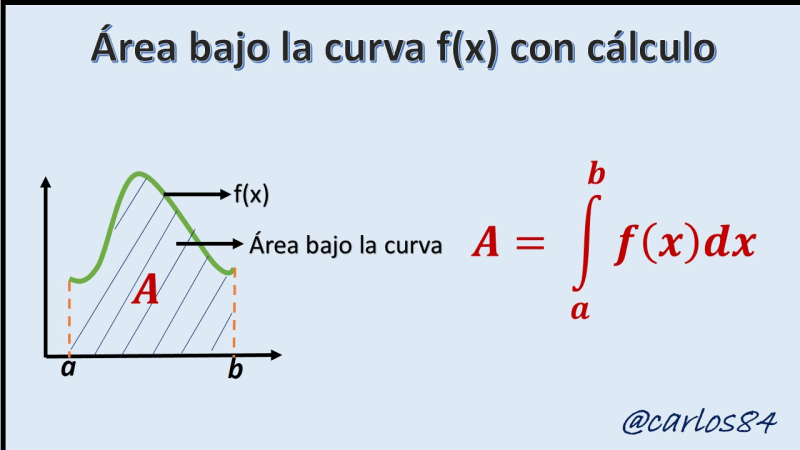
[4] Una de las preocupaciones para los que estudian la geometría en la antigüedad era el cálculo del área, ya que para calcular el área de ciertos cuerpos geométricos conocidos como rectángulos, triángulos, entre otros, resultaba fácil realizar estos cálculos de área, sin embargo cuando se analiza la idea de calcular el área bajo la curva se necesita el cálculo integral, ya que con las matemáticas previas al cálculo esto resultaba imposible.

^{Autor de la imagen @ carlos84}

Conclusiones y lecciones aprendidas

Para cada uno de los ejemplos explicados en la que especifica la situación tiene una solución distinta con las matemáticas previas al cálculo, y otras se resuelven con la aplicación del cálculo diferencial e integral, tienen una reforma de transición, es decir una etapa de transición entre las matemáticas previas al cálculo y el cálculo, esta etapa de transición es el proceso de límite, con lo que podemos concluir que otra forma de conceptualizar el cálculo es decir que el cálculo es una máquina de generar límites que funciona en tres bloques o etapas, tal y como lo presento a continuación:

^{Autor de la imagen: @ carlos84}

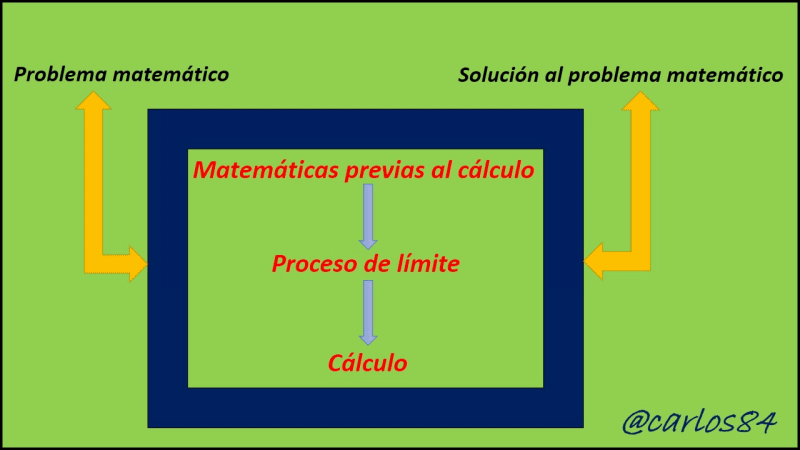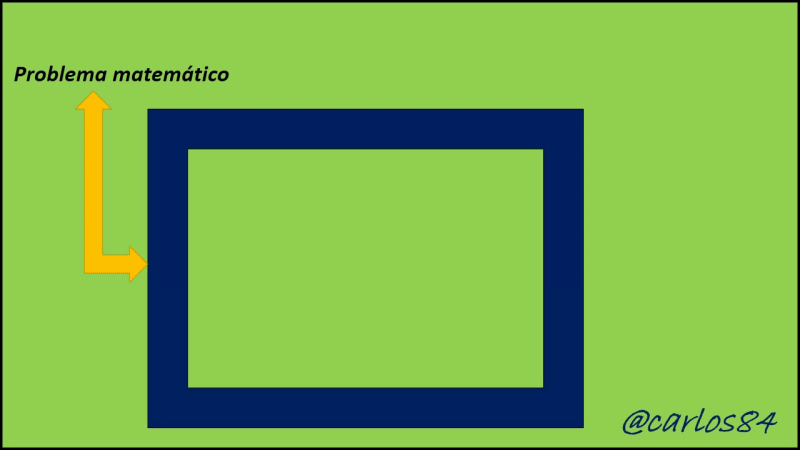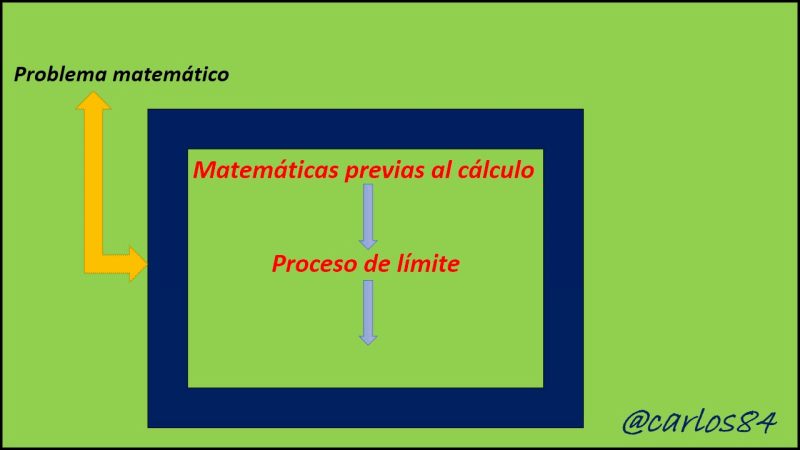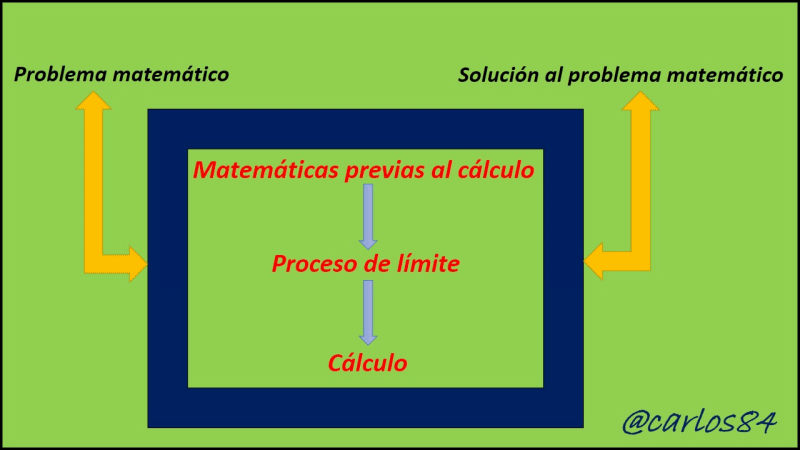
Bajo este esquema, quizás Newton y Leibniz atacan los problemas que para la antigüedad no se resolverán con las matemáticas previas al cálculo, una vez sentadas las bases del cálculo se puede pensar en abordar cualquier problema bajo estos tres bloques, teniendo primeramente como matemáticas previas al cálculo a todo aquel conocimiento base que englobe a la pendiente de una recta conociendo dos puntos, área de un ángulo, entre otros. El segundo gran bloque lo abarca el proceso de límite como ese proceso de transición entre las matemáticas previas al cálculo y el cálculo propio, y como tercer y último bloque tenemos al cálculo infinitesimal como el final de los procesos en el que se cuenta como una nueva herramienta con formulación propia basada en términos de diferenciación e integración, es decir en derivadas e integrales.

Cuando el estudio del cálculo no se centra en un análisis profundo que siente sus raíces y orígenes en los problemas de la antigüedad, se puede caer en el error de trazar objetivos erróneos en el proceso de enseñanza - aprendizaje del cálculo, tal es el caso ocurrió cuando se pretende ver y entender al cálculo como si se trata de un nuevo aprendizaje que solo amerita aprender un conjunto de fórmulas nuevas.

Estamos en la obligación de innovar sobre el estudio del cálculo, de romper los paradigmas tradicionales que hacen ver erróneamente al cálculo como esa fuente de conocimiento en la que solo se amerita la memorización de fórmulas de derivadas e integrales, que a mi parecer puede inducir al Desinterés y falta de comprensión, lo que podría desencadenar en una falta de confianza en el aprendizaje del cálculo sin ningún tipo de satisfacción en su aprendizaje.

Espero haber cubierto los objetivos básicos que me propuse para este post, el cual es generar la confianza necesaria en el lector para adentrarse en el estudio y la comprensión del cálculo, partiendo de la premisa de algunos concejos que se describen en el inicio del artículo, y También se puede realizar el cálculo del mar visto bajo un análisis profundo que vaya más allá de entenderlo como un conjunto de fórmulas para aplicar para resolver límites, derivadas e integrales.

Referencias consultadas y recomendadas

[1] Libro de cálculo con Geometría analítica. Autor: Ron Larson y Robert P. Hostetler. 8va edición.

[2] Libro de cálculo. Autor: Louis Leithold. 7ma edición.

__________________________________________________________________________________________________________________________________

"Para toda aquella persona que le apasiona la matemática, física, química, biología, educación e ingeniería, le recomiendo la etiqueta de # stem-español, es una comunidad que valora el contenido intelectual y académico de calidad, conservando siempre la originalidad de las "Publicaciones, por lo que se recomienda a todos aquellos amigos de Steemit que deseen publicar utilizando esta etiqueta a no cometer plagio".