Diagramas cartesianos de desplazamiento en sistemas materiales de 1 grado de libertad
¡Saludos estimados lectores! como continuación a la anterior publicación, ahora se abordarán los diagramas cartesianos de desplazamiento en cadenas cinemáticas de 1 grado de libertad. Este contenido es la continuación del siguiente artículo:
•Diagramas cartesianos de desplazamiento y aplicación al principio de los trabajos virtuales
En el cual se abordaron los diagramas cartesianos de desplazamiento para sistemas de solo una chapa con un (1) grado de libertad (1 GL). Esta vez nos referimos a un sistema de 1 GL de varias chapas vinculadas entre sí (cadena cinemática de 1 GL).
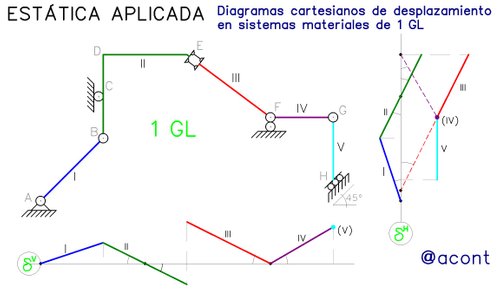
Introducción
La representación gráfica de la desplazabilidad de una chapa de un (1) grado de libertad en el plano, puede realizarse mediante los diagramas cartesianos de desplazamiento horizontales y verticales, ya sea que la chapa rota alrededor de un polo o presente traslación pura. En la anterior publicación, se abordó la aplicabilidad de este procedimiento gráfico para determinar reacciones en sistemas isostáticos sometidos a un sistema de cargas externas, como alternativa a las ecuaciones de equilibrio estático, mediante el principio de los trabajos virtuales para cuerpos rígidos. Dicha aplicabilidad se basa en la determinación gráfica y exacta de los desplazamientos virtuales. Adicionalmente, se realizó una demostración del principio del trabajo virtual para un sistema material de solo una chapa sometida a cargas externas.
Por otro lado, existen sistemas materiales isostáticos que poseen dos o mas chapas vinculadas entre sí. Recordemos que la aplicación del principio del trabajo virtual para cuerpos rígidos (P.T.V.C.R.) conlleva transformar el sistema original (de GL=0) en un “sistema equivalente virtual” de 1 GL al eliminar una de sus restricciones. Dicho sistema virtual es una cadena cinemática de 1 GL de chapas vinculadas entre sí, y los desplazamientos virtuales que esta presenta deben ser determinados elaborando los diagramas cartesianos de desplazamiento, para así llevar a cabo la sumatoria de trabajos virtuales que las cargas realizan sobre el sistema. En este sentido, se llevará a cabo en la presente publicación un abordaje práctico sobre la realización de dichos diagramas sobre un sistema material de 1 GL que posee varias chapas vinculadas entre sí.
Primer paso: búsqueda de polos del sistema material
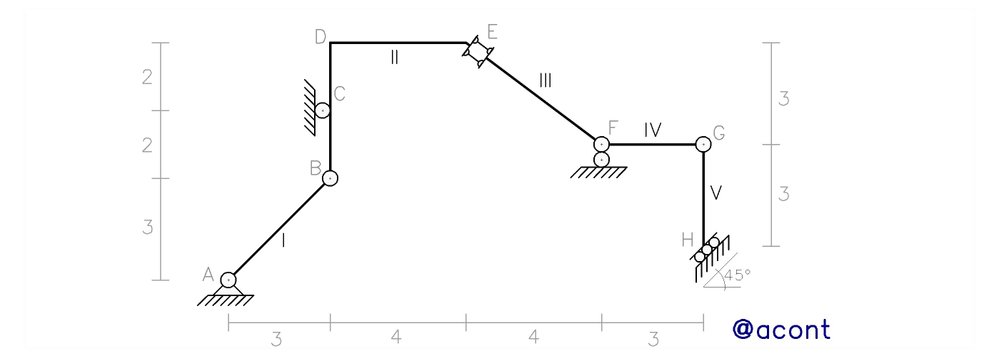
Podemos asumir que el siguiente sistema material es el resultado de eliminar una restricción a un sistema isostático estable (GL=0), resultando así en un sistema material de 1 GL (Fig. N°1).
Podemos verificar lo anterior mediante la ecuación utilizada para determinar los grados de libertad de sistemas materiales. La Ecuación (3) del artículo Determinación Algebraica de los Grados de Libertad de Sistemas Materiales en Estática Aplicada y Ejemplo de Aplicación nos ayuda a realizar esto:

De acuerdo a la Fig. N°1, el número “n” de chapas es cinco (5). El número de unidades de vinculación externas es seis (6) (2 para la articulación fija a tierra en “A”, 1 para cada apoyo simple “rodillo” en “C” y “F” y 2 para el empotramiento móvil en “H”). Y el número de unidades de vinculación internas es ocho (8) (2 para cada rótula en “B”, “F” y “G” y 2 para las bielas paralelas en “E”). En esta publicación se puede encontrar más información acerca de los vínculos y sus unidades de vinculación. De esta manera aplicamos la ecuación:
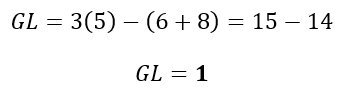
Una vez verificado esto, podemos ubicar los polos del sistema material. Si el sistema posee 2 o más grados de libertad, será imposible definir el polo de una o más chapas del mismo y su movimiento es indefinido o impredecible. Solo se pueden definir por completo los polos de sistemas materiales de 1 GL, por lo tanto, es posible describir de manera exacta su movimiento. En la Fig. N°2 se han hallado los polos del sistema material dado.
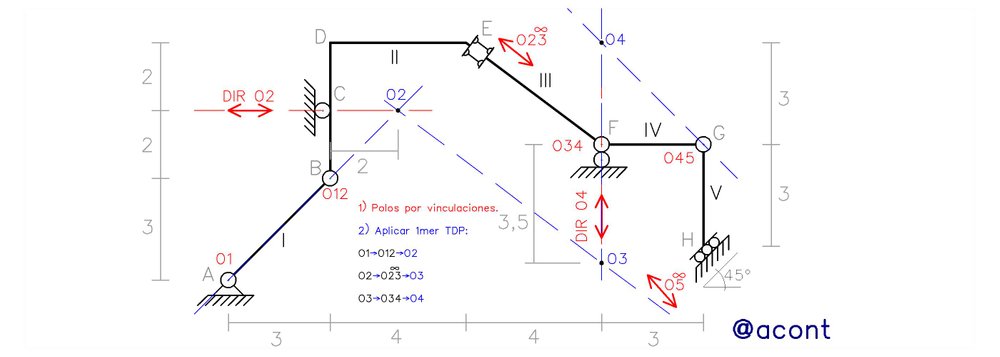
En este artículo se puede encontrar más información acerca del primer Teorema de los Polos (1mer TDP) y su aplicación en la búsqueda de los mismos. Una vez hallados los polos, podemos empezar a elaborar los diagramas cartesianos de desplazamiento.
Trazado de los diagramas cartesianos
Sobre ambos ejes cartesianos, debemos proyectar los polos del sistema material. En el caso de las chapas que poseen polo en el infinito, las mismas presentan traslación pura, y sabemos que sus diagramas de movimiento serán paralelos a los ejes cartesianos, por ello, para la chapa V no se proyectará ningún polo sobre dichos ejes (Fig. N°3).
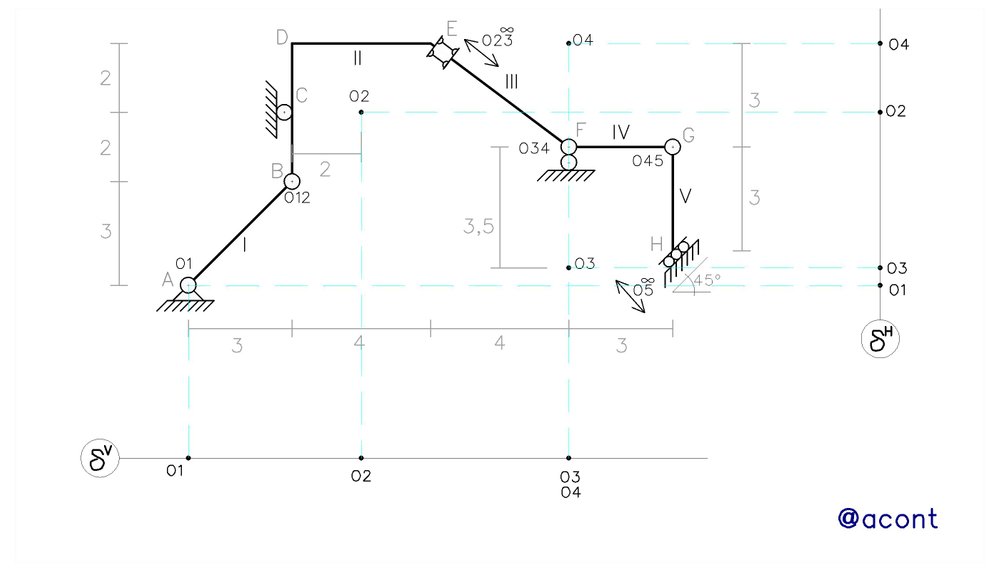
Debemos asignar una rotación arbitraria “α” a alguna de las chapas del sistema material, de manera que los desplazamientos y rotaciones del resto de chapas estarán expresados en función de “α”. Usualmente, lo más simple y práctico sería asignar esta rotación a alguna chapa que se encuentre articulada a tierra, como es el caso de la chapa I. Para este ejemplo, le asignaremos esta rotación a la chapa I en sentido antihorario.
Como resultado de la rotación infinitésima “α”, podemos representar la rotación de la chapa I en los diagramas cartesianos, mediante una línea recta que parte de la proyección de su polo sobre ambos ejes. Al ser esta rotación de orden infinitesimal, podemos asumir que su tangente es igual a su magnitud, por lo tanto, los desplazamientos horizontal y vertical del punto “B” representados en los ejes cartesianos, serán simplemente el producto del ángulo “α” por la distancia vertical y horizontal respectivamente (Fig. N°4).
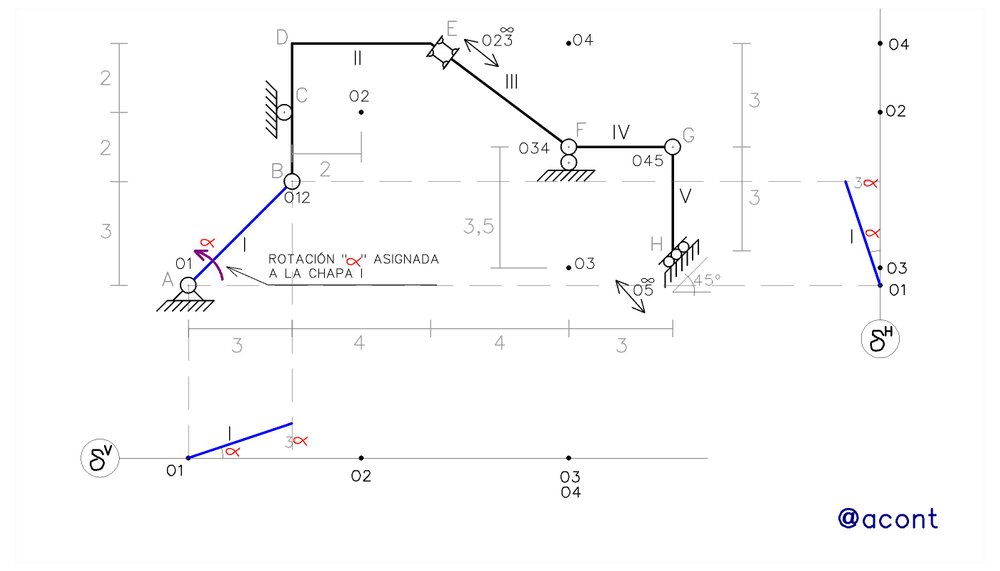
Ahora, debemos realizar los diagramas cartesianos de desplazamiento de la chapa II. Sabemos que estos diagramas serán siempre rectas. La vinculación entre las chapas I y II viene dada por una rótula (articulación interna), por lo que esta vinculación en “B” representa un punto que ambas tienen en común y que además presenta un único desplazamiento. Lo anterior indica que, en los diagramas cartesianos, ambas chapas también deben vincularse en dicho punto ya que presenta el mismo desplazamiento para ambas. Adicionalmente, se conoce la proyección del polo de dicha chapa, por lo que conocemos dos puntos por los que trazar su diagrama. El diagrama se traza hasta donde sea posible proyectar la chapa, en este caso, el punto “E” es el último punto proyectable para la chapa II si la observamos de izquierda a derecha y de abajo hacia arriba (Fig. N°5).
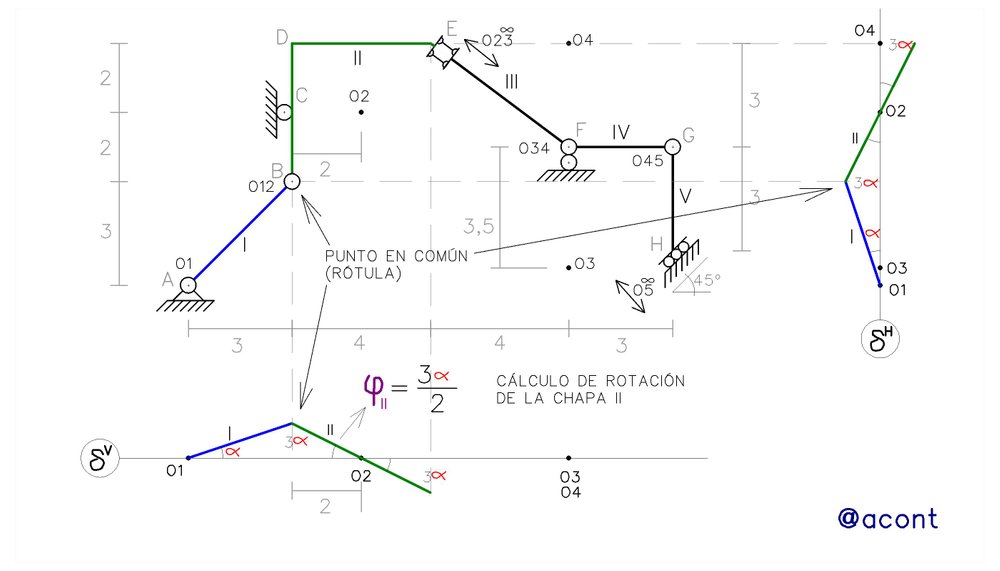
Para poder representar los diagramas cartesianos de la chapa III, debemos notar la presencia de bielas paralelas como vinculación interna entre esta y la chapa III. Del artículo ESTÁTICA APLICADA: bielas paralelas en sistemas materiales de 1 grado de libertad Parte I, sabemos que las bielas paralelas limitan ambas chapas vinculadas a rotar en igual magnitud y sentido, esto indica que en los diagramas cartesianos ambas chapas serán paralelas, ya que rotan exactamente igual y por lo tanto los diagramas cartesianos de la chapa III pasarán por la proyección de su polo y serán paralelos a los de la chapa II. Por otro lado, el punto “E” puede subdividirse en un punto “E2” y un punto “E3” para las chapas II y III respectivamente, ya que, debido a las bielas paralelas, se presenta distinto movimiento del punto “E” para ambas chapas. Todo esto se ilustra en la Fig. N°6.
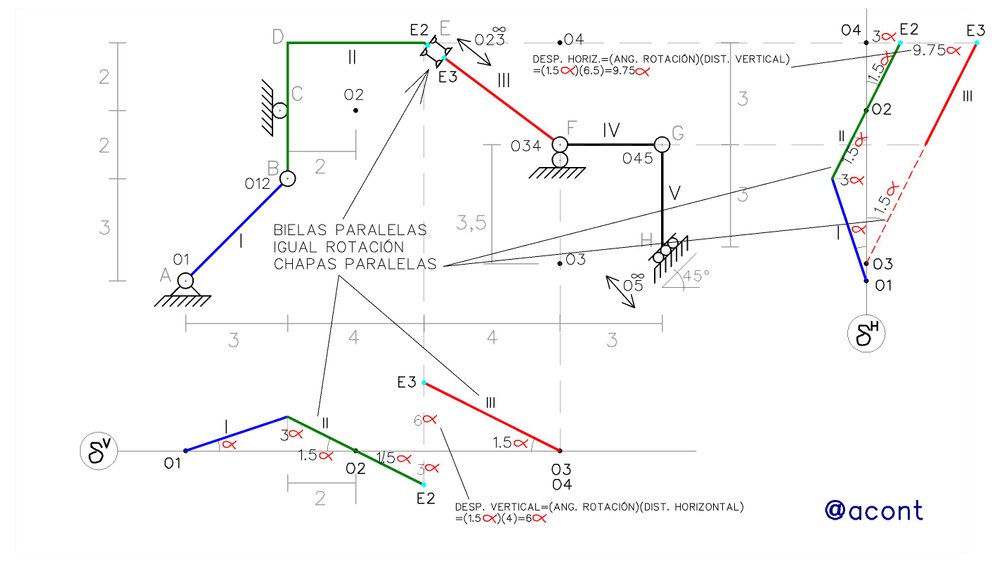
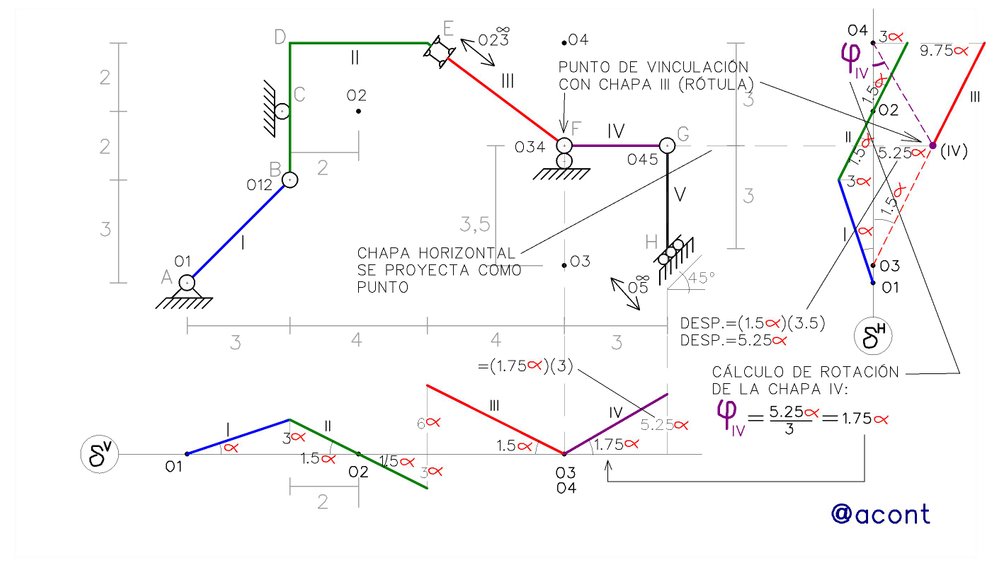
Ya que no conocemos el ángulo de rotación de la chapa IV, no podemos empezar por su diagrama cartesiano de desplazamientos verticales, sino que nos vamos al otro eje cartesiano, donde podemos apreciar su punto de vinculación con la chapa III, el cual es mediante una rótula (similar al caso entre las chapas I y II). Debemos notar que la chapa IV se proyecta sobre el diagrama cartesiano de desplazamientos horizontales como un punto, y que además el polo se encuentra fuera de su proyección, por lo que se traza mediante líneas discontinuas su diagrama uniendo su proyección como punto a la proyección de su polo. De esta manera podemos determinar el ángulo de rotación de esta chapa y trazar su diagrama cartesiano de desplazamientos verticales (Fig. N°7).
Finalmente, la chapa V tiene su polo absoluto en el infinito, por lo que esta presenta traslación pura. La dirección de esta traslación se da en la dirección que permite el empotramiento móvil del punto “H”, es decir, con una inclinación de 45° respecto a la horizontal. En consecuencia, los diagramas cartesianos de la chapa V serán paralelos a los ejes cartesianos, ya que todos los puntos sobre dicha chapa presentan igual magnitud y dirección de desplazamiento. El punto “G” representa la ubicación de la vinculación entre las chapas IV y V. Similar a los casos anteriores (rótulas en “B” y “F”), la rótula en “G” es un punto común a ambas chapas y presenta un único desplazamiento, de esta manera, solo debemos trazar a partir de este punto una recta paralela a los ejes cartesianos. Sin embargo, debemos notar que la chapa V se proyecta verticalmente como un punto, teniendo como resultado que, en el diagrama cartesiano de desplazamientos verticales, no veamos una recta paralela al eje cartesiano horizontal sino solo un punto (Fig. N°8).
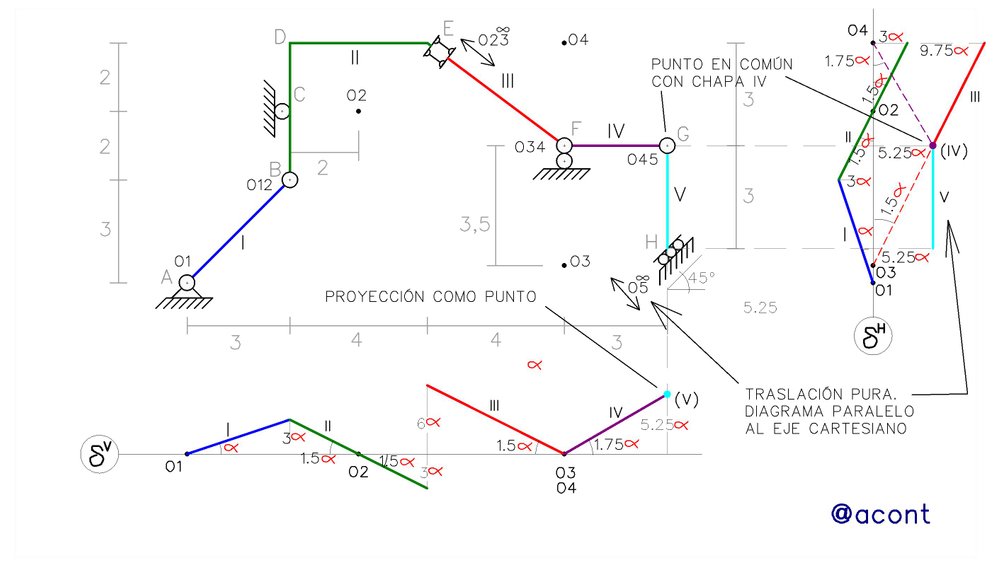
Ya hemos elaborado los diagramas cartesianos de desplazamiento al sistema material para cada una de las chapas. De esta manera, podemos observar de manera gráfica como se dan los desplazamientos de todos los puntos del sistema y la magnitud y sentido de la rotación de todas las chapas del mismo en función de una rotación inicial “α” (Fig. N°9).

De igual manera, podemos calcular el desplazamiento de un punto específico si conocemos su ubicación exacta en el sistema material, ya que basta con conocer la distancia del mismo al polo de la chapa sobre la cual se encuentra. Para ilustrar esto vamos a calcular el desplazamiento de cuatro puntos específicos mostrados en la Fig. N°10.

No solo hemos representado gráficamente el movimiento de la cadena cinemática de 1 GL, sino que podemos determinar con exactitud el desplazamiento de sus puntos, sin olvidar que estamos asumiendo que las rotaciones son de orden infinitesimal y solo tomamos en cuenta la componente tangencial del desplazamiento producto de la rotación alrededor de un polo.
En la próxima publicación se abordará el diagrama auxiliar, procedimiento empleado cuando se tienen bielas paralelas como vinculación interna entre dos chapas que al mismo tiempo están sometidas a traslación pura. De esta manera, nos acercamos al tema del Principio del Trabajo Virtual para Cuerpos Rígidos, donde estos diagramas sirven de herramienta en el cálculo de reacciones externas de sistemas isostáticos.
Conclusiones
Referencias Bibliográficas
[1]Hernández, Suilio. (1998). Estática Aplicada. Folleto Editado por el Departamento de Ingeniería Estructural U.C.V. Caracas.Fuente
[2]Rodríguez, Iván. (2003). Estática de las Estructuras.Fuente
Material recomendado
•@acont. ESTÁTICA APLICADA: análisis por movimiento infinitésimo de sistemas materiales de 1 grado de libertad
•@acont. Diagramas cartesianos de desplazamiento y aplicación al principio de los trabajos virtuales
Imágenes y ecuaciones de autoría propia realizadas mediante LibreCAD y Microsoft Word.
Ing. Ángel Contreras
De acuerdo a la Biblia, ¿Tiene la Biblia contradicciones, o algunas iglesias la malinterpretan?
Mira el video a continuación para saber la respuesta ...
(Perdón por enviar este comentario. No estamos buscando nuestro beneficio propio, su intención es predicar las palabras de Dios de cualquier manera posible).
Comenta lo que entiendes de nuestro video de Youtube para recibir nuestros votos completos. Tenemos 30,000 #SteemPower. Es nuestra pequeña forma de Gracias, nuestro querido amigo.
Mira nuestra Discord Chat
Únete a nuestra comunidad oficial: https://steemit.com/created/hive-182074
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having used the steemstem.io app and included @steemstem in the list of beneficiaries of this post. This granted you a stronger support from SteemSTEM.
Congratulations @acont! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness to get one more award and increased upvotes!