Saludos queridos lectores, bienvenidos nuevamente. En esta oportunidad les traigo la 12^va y última Lección de la serie Introducción a las Ecuaciones Diferenciales Parciales (EDP), en la misma hablaremos acerca las ecuaciones diferenciales parciales de 2^do orden, en dos o mas variables independientes y del principio de superposición de soluciones.

El tema de las Ecuaciones Diferenciales Parciales es un tema de mucho interés en diversos campos o áreas, como lo son: la física, la química, la biología, la ingeniería en todas sus ramas o carreras afines y otras ciencias. En la gama de problemas que se modelan con Ecuaciones Diferenciales Parciales, podemos mencionar algunos como: la propagación del calor, la propagación del sonido, la dinámica de fluidos, entre otros. La misma está dirigida al público en general (aunque debemos acotar, este es un tema de un nivel más alto, para el que es necesario tener de algunos conocimientos previos de análisis real, ecuaciones diferenciales ordinarias, geometría diferencial, cálculo avanzado, entre otros más), con atención especial a profesionales y estudiantes universitarios en ciencias, ingeniería y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

---

---

Ecuaciones Diferenciales Parciales de 2^do Orden en dos o más Variables Independientes

Una ecuación diferencial parcial lineal de 2^do orden en n variables independientes es una ecuación de la forma siguiente

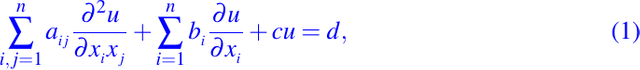
donde los coeficientes a_ij, b_i, c y d en la ecuación anterior son funciones que dependen de las variables independientes x₁, x₂, . . . , x_n. Como en el caso de dos variables independientes, la ecuación dada en (1) se puede clasificar de acuerdo a una cierta propiedad de la matriz de coeficientes [a_ij] y la parte principal. Ya que


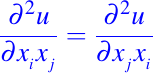
podemos asumir sin perdida de generalidad que [a_ij] es simétrica, es decir, que a_ij = a_ji, para valores de i, j = 1, . . . ,n. La propiedad, la cual se puede usar para clasificar la ecuación dada en (1), debe ser tal que permanezca invariante bajo transformaciones de coordenadas suaves no singulares.

Para la ecuación dada por

en dos variables independientes la propiedad usada para su clasificación tiene que ver con el signo de el discriminante


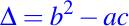
Tal y como lo mostramos en la Lección #11, el signo del discriminante es invariante bajo transformaciones de coordenadas suaves y no singulares. La matriz de coeficientes de la parte principal de la ecuación dada en (2) es


Los valores propios de esta matriz son las raíces de la ecuación


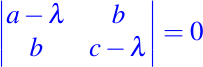
ó


Sean λ₁ y λ₂ las raíces de la ecuación mostrada en (4). Es fácil chequear que λ₁ y λ₂ son reales (de hecho los valores propios de la matriz simétrica son siempre reales) y que


ó


De la ecuación (4) podemos concluir que

1. Si el discriminante es mayor que cero, es decir, positivo si y solamente si las dos raíces son distintas de cero y tienen signos opuestos.
2. Si el discriminante es igual a cero, si y solamente si al menos una de las dos raíces es igual a cero.
3. Si el discriminante es menor que cero, es decir, negativo si y solamente si las dos raíces son distintas de cero y tienen signos iguales.

Podemos clasificar las ecuaciones diferenciales parciales de segundo orden en dos variables independientes de acuerdo al signo de los valores propios de los coeficientes de la matriz de la parte principal. De hecho, este es el esquema de clasificación que usaremos para las ecuaciones diferenciales parciales de segundo orden en dos o más variables independientes.

Los valores propios de la matriz de coeficientes [a_ij] están definidos por las raíces de la ecuación

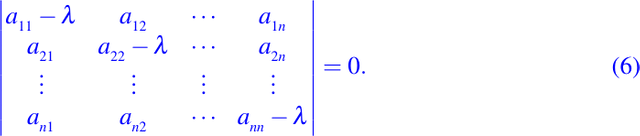
Sabemos del álgebra lineal, que el hecho de que [a_ij] es simétrica, su valores propios son todos reales. Además, usando un teorema de álgebra lineal, podemos mostrar que, en un punto en particular x⁰, el número de valores propios, positivos, negativos o ceros de la parte principal de la ecuación (1) resultan invariantes bajo transformaciones de coordenadas suaves no singulares. Esto muestra el esquema de clasificación siguiente para ecuaciones diferenciales parciales de segundo orden independientes del sistema de coordenadas particulares usado.

---

---

Ejemplos

1. La ecuación de Laplace
   
   
   es elíptica en Rⁿ.
2. La ecuación de onda
   
   
   donde x_n representa a la variable del tiempo t, es hiperbólica en Rⁿ.
3. La ecuación
   
   
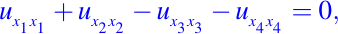
   es ultra hiperbólica en R⁴.
4. La ecuación del calor
   
   
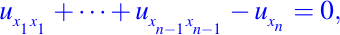
   donde x_n representa a la variable del tiempo t, es parabólica en Rⁿ.

---

---

Como vimos en la Lección #11 que al hacer una transformación de coordenadas, cualquier ecuación diferencial parcial de segundo orden en dos variables independientes puede ser reducida a su forma canónica en todo entorno de cualquier punto. En general, esto no puede realizarse para ecuaciones con coeficientes variables en mas de dos variables independientes. Sin embargo, usando un teorema del álgebra lineal podemos mostrar que esto es siempre posible si hacemos una transformación de coordenadas lineales y reducimos la ecuación (1) a la forma canónica en cualquier punto dado. La forma canónica es tal que la matriz de coeficientes de su parte principal es diagonal en el punto. Explícitamente, si podemos mostrar que para cualquier punto dado P en Rⁿ hay una transformación lineal

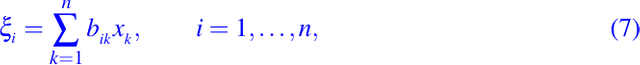
tal que en términos de las nuevas coordenadas ξ₁, . . . ,ξ_n, la ecuación (1) tiene la forma


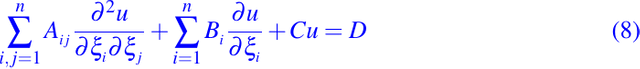
donde en P el valor de los coeficientes A_ij son


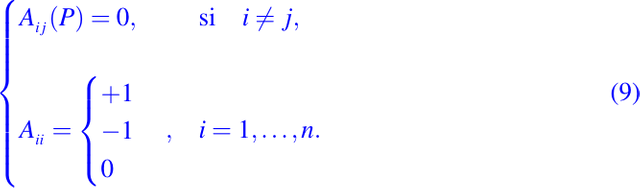
Además los números


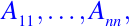
difieren de los valores propios de la matriz de coeficientes [a_ij(P)] solo por factores positivos.
Debemos resaltar que si los coeficientes a_ij de la ecuación (1) son variables, los coeficientes A_ij de (8) son también variables y tiene los valores dados por (9) solamente en el punto dado P y no necesariamente en cualquier otro punto P. Si acaso los coeficientes a_ij son constantes, los coeficientes A_ij también son constantes y tenemos la forma canónica la cual es válida en todas partes.

Así podemos enunciar el siguiente teorema

---

---

Ahora mostraremos las formas de las ecuaciones elípticas, hiperbólicas y parabólicas de segundo orden más comunes que se originan a partir de problemas físicos. Para ello, necesitamos la siguiente definición

Un teorema conocido del álgebra lineal afirma que los valores propios de una matriz simétrica [a_ij] son todos positivos si y solamente si, la forma cuadrática asociada con [a_ij] es definida positiva. En vista de este teorema la siguiente definición de elípticidad en un dominio Ω es equivalente a la definición dada previamente. Asumimos que el signo en frente de la ecuación (1) es elegido para que a₁₁ > 0 en un dominio Ω, la ecuación (1) es llamada elíptica en Ω si la forma cuadrática

es definida positiva para cualquier punto x de Ω.

La ecuación elíptica de segundo orden, usualmente aparece en el estudio de problemas físicos relacionados con fenómenos de estados estacionarios. Por ejemplo, si u(x) es la temperatura en el estado estacionario en el punto x de un cuerpo isótropico no homogéneo, entonces en cualquier punto interior de el cuerpo, u debe satisfacer la ecuación elíptica de segundo orden

La función k(x) es siempre positiva y es llamada el coeficiente de la conductividad termal de el cuerpo en el punto x. Si el cuerpo es homogéneo, k(x) es constante y la ecuación dada en (16) se convierte en la ecuación de Laplace.

El fenómeno de propagación de onda tales como la propagación del sonido o de ondas electromagnéticas las ondas son frecuentemente descritas por ecuaciones hiperbólicas de segundo orden de la forma general siguiente

donde los puntos representan los términos de menor orden que 2 y la forma cuadrática asociada con la matriz [a_ij] es definida positiva.

En la ecuación (17) tenemos n + 1 variables independientes, n variables espaciales, x₁, x₂, . . . , x_n y una variable del tiempo t. Es fácil verificar, que la ecuación mostrada en (17) es hiperbólica, de acuerdo con la Definición (1) dada anteriormente.

Fenómenos tales como el flujo de calor o la difusión de un fluido a través de medios porosos son usualmente descrito por ecuaciones parabólicas de segundo orden de la forma general siguiente

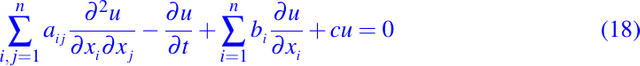
donde la forma cuadrática asociada con la matriz [a_ij] es definida positiva. En la ecuación (18) tenemos n + 1 variables independientes. Observemos cuidadosamente el papel especial de la variable del tiempo t. La parte principal de la ecuación no involucra derivadas con respecto a t y el coneficiente de la derivada de primer orden con respecto a t es -1. La ecuación (18) es obviamente parabolica de acuerdo a la Definición 1, dada anteriormente, y debido a su característica especial es algunas veces llamada parabólica en el sentido estricto.

Podemos mencionar tambien algunas observaciones sobre las superficies características de las ecuaciones de segundo orden. Notemos primero que si la ecuación dada en (1) es elíptica esta no tiene superficies características. En efecto, un vector no nulo, digamos ξ =(ξ₁,ξ₂, . . . , ξ_n) de Rⁿ define una dirección la cuál es característica on respecto a la ecuación dada en (1) si

Usando la definición de elípticidad en términos de la definición de positividad de la forma cuadrática asociada con [a_ij] vemos que (19) no se satisface para un vector no nulo ξ. Por lo tanto, las ecuaciones elípticas de segundo orden no tienen direcciones características y por lo tanto no tiene superficies características. Esta propiedad de no existencia de características es usada para definir ecuaciones diferenciales parciales lineales elípticas de cualquier orden.

Considere ahora la ecuación parabólica de la forma (18). Un vector no nulo ξ =(ξ₁,ξ₂, . . . , ξ_n, ξ_t) de Rⁿ⁺¹ define una dirección la cual es característica con respecto a (18) si (19) se satisface. De nuevo, la definición de positividad de la forma cuadrática en (19) implica que ξ₁ = ξ₂ = . . . = ξ_n = 0 y por lo tanto, ξ =(ξ₁,ξ₂, . . . , ξ_n, ξ_t) = (0, 0, . . . , 0, 1) es la única dirección característica de (18). Así, el hiperplano f = constante es la única superficie característica de (18).

La característica de la ecuación hiperbólica de la forma dada en (17) son más complicadas. Un vector no nulo ξ =(ξ₁,ξ₂, . . . , ξ_n, ξ_t) de Rⁿ⁺¹ define una dirección la cual es característica con respecto a (17) si

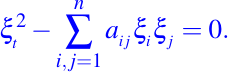
Existen infinitas direcciones las cuales satisfacen la ecuación y la estructura de las superficies características es aún más complicadas por el factor que los coeficientes a_ij pueden ser funciones de x. La ecuación de onda es un caso especial de la ecuación dada en (17), en cada punto de Rⁿ⁺¹ es el ápice de un cono característico de la ecuación de onda.

---

---

El Principio de Superposición

Sea P = P(x,D) un operador diferencial parcial lineal de orden m en Rⁿ, dado por

Usando el hecho familiar que cualquier multi-índice


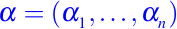
y cualquier constantes c₁ y c₂,


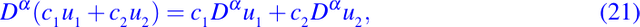
es fácil verificar que


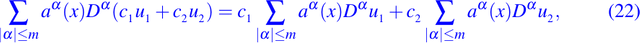
o más brevemente,

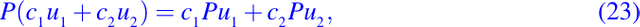
En las ecuaciones dadas por (21) - (23) las funciones u₁ y u₂ son cualquiera dos funciones las cuales son suficientemente diferenciables.

En el lenguaje de álgebra lineal la relación dada en (23) puede ser expresada por diciendo que P acutua en la función u como una transformación lineal. Más precisamente, si consideramos solo la función u de clase C^m sobre un dominio Ω de Rⁿ, entonces P es una transformación lineal de el espacio de vectores C^m(Ω) en el espacio de vectores C⁰(Ω).

Como una consecuencia de la propiedad de linealidad (23) de P, las soluciones de la ecuación homogénea

tiene la siguiente propiedad de superposición: Si u₁ y u₂ son dos soluciones cualesquiera de la ecuación homogénea (24) y c₁ y c₂ son constantes arbitrarias, entonces la combinación lineal c₁u₁ + c₂u₂, es también una solución de (24). En lenguaje algebracio esta propiedad de superposición puede ser expresada diciendo que las soluciones de (24) forman un espacio vectorial.

La propiedad de superposición obviamente se mantiene para cualquier numero finito de soluciones de la ecuación homogénea dada en (24). Si u₁, u₂, . . . ,u_k son soluciones y c₁, c₂, . . . ,c_k son constantes arbitrarias, entonces

es también una solución. La combinación lineal dada en (25) es llamada una superposición de las soluciones u₁, u₂, . . . ,u_k. Ya que las constantes c₁, c₂, . . . ,c_k pueden esogerse arbitrariamente, formando superposiciones de una colección conocida de soluciones de la ecuación (24), obteniendo una gran colección de nuevas soluciones.

Como un ejemplo, consideremos la ecuación de Laplace en R²,

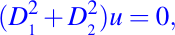
ó


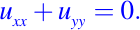
Es fácil verificar que las funciones


son soluciones de la ecuación. Por superposición, todos los polinomios


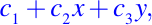
de grado menor o igual a 1 son también soluciones de la ecuación.

Es natural intentar formar superposiciones de un numero infinito de soluciones de (24). Sean u₁, u₂, . . . de soluciones de la ecuación (24) y suponiendo que la serie

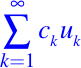
converge. Entonces la función


es también una solución de la ecuación (24) siempre que


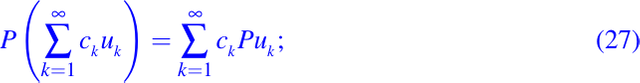
es decir, siempre que P se pueda aplicar a la serie termino por término.

También podemos partir de superposiciones de una familia de soluciones de un parámetro de (24). Supongamos que para cada valor de un parámetro λ en algún interbalo I de R, la función u(x, k) es una solución de (24), es decir,

Supongamos además que para una función de valores reales g definida en I, la integral

es convergente. Entonces la función


es también una solución de (24) siempre que


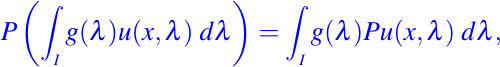
es decir, siempre que el orden de aplicación de P y de integración con respecto al parámetro λ se pueden intercambiar. También podemos formar superposiciones de soluciones de (24) dependiendo de varios parámetros.

Finalmente sea u(x, λ), con λ en I sea una familia a un parámetro de soluciones de (24) y consideremos la superposición

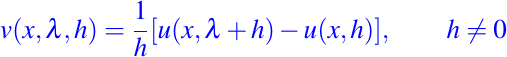
las cuales son soluciones de (24) dependientes también de el parámetro h. Supongamos que el límite


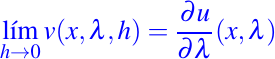
existe. Entonces la función


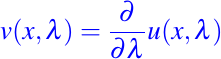
es también solución de (24) siempre que

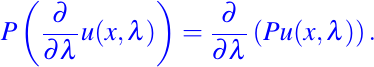
Todos estos métodos de superposición, cuando ellos son validos, nos permite extender una colección conocida de soluciones de una ecuación homogénea a una colección de soluciones más grande.

Debemos señalar que el principio de superposición no es valido para ecuaciones diferenciales parciales que no sean lineales. Por esta razón, es mucho mas complicado obtener soluciones de ecuaciones diferenciales parciales no lineales.

---

---

Queridos amigos y lectores, espero hayan disfrutado y aprendido en esta 12^va y última Lección de la serie de Introducción a las Ecuaciones Diferenciales Parciales, donde hemos sido bastante amplio en el tema, espero que esta serie pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:

• Lang, Serge. Calculus of Several Variables. Springer Science & Business Media, 2012.
• Edwards, Charles Henry. Advanced Calculus of Several Variables. Courier Corporation, 2012.
• Dennemeyer, Rene. Introduction to Partial Differential Equations and Boundary Value Problems. 1968.
• Pinchover, Yehuda, and Jacob Rubinstein. An Introduction to Partial Differential Equations. Cambridge University Press, 2005.

---

También los invito a leer las anteriores publicaciones de está serie de Introducción a las Ecuaciones Diferenciales Parciales, que estoy seguro serán de su interés:

Introducción a las Ecuaciones Diferenciales Parciales - Lección #1	Introducción a las Ecuaciones Diferenciales Parciales - Lección #2
Introducción a las Ecuaciones Diferenciales Parciales - Lección #3	Introducción a las Ecuaciones Diferenciales Parciales - Lección #4
Introducción a las Ecuaciones Diferenciales Parciales - Lección #5	Introducción a las Ecuaciones Diferenciales Parciales - Lección #6
Introducción a las Ecuaciones Diferenciales Parciales - Lección #7	Introducción a las Ecuaciones Diferenciales Parciales - Lección #8
Introducción a las Ecuaciones Diferenciales Parciales - Lección #9	Introducción a las Ecuaciones Diferenciales Parciales - Lección #10
Introducción a las Ecuaciones Diferenciales Parciales - Lección #11	Introducción a las Ecuaciones Diferenciales Parciales - Lección #12

---

Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, , GIMP e Inkscape.

---

---

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.

_{Imagen diseñada con GIMP y elaborada por @abdulmath.}