Introducción a las Ecuaciones Diferenciales Parciales | Lección #11

El tema de las Ecuaciones Diferenciales Parciales es un tema de mucho interés en diversos campos o áreas, como lo son: la física, la química, la biología, la ingeniería en todas sus ramas o carreras afines y otras ciencias. En la gama de problemas que se modelan con Ecuaciones Diferenciales Parciales, podemos mencionar algunos como: la propagación del calor, la propagación del sonido, la dinámica de fluidos, entre otros. La misma está dirigida al público en general (aunque debemos acotar, este es un tema de un nivel más alto, para el que es necesario tener de algunos conocimientos previos de análisis real, ecuaciones diferenciales ordinarias, geometría diferencial, cálculo avanzado, entre otros más), con atención especial a profesionales y estudiantes universitarios en ciencias, ingeniería y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

Formas Canónicas de Ecuaciones Diferenciales Parciales de 1er Orden.
Consideremos la ecuación diferencial parcial de 1er orden en dos variables, dada por la ecuación

donde los coeficientes a(x,y), b(x,y), c(x,y) y d(x,y) son funciones que están definidas en Ω de R2. Asumimos que a(x,y) y b(x,y) son funciones de clase C1 sobre Ω y las cuales no se anulan simultaneamente sobre cualquier punto de Ω. Nosotros mostraremos que en un entorno U de cualquier punto (x0,y0) de Ω, podemos introducir nuevas coordenadas ξ y η en sus término para lo cual la ecuación diferencial parcial dada en la ecuación (1) toma la forma siguiente
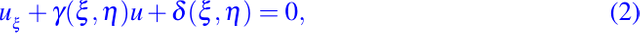
así, en las nuevas coordenadas la ecuación diferencial parcial dada en (1) se convierte en una ecuación diferencial ordinaria con ξ como una variable independientes y η como un parámetro en cual puede ser tratado como una constante. La ecuación mostrada en (2) es llamada la forma canónica de la ecuación dada en (1). También podemos decir que (ξ, η) son las coordenadas de la ecuación en la forma canónica. Frecuentemente la forma canónica dada por (2) puede ser fácilmente integrada y después regresamos a la coordenadas originales x y y, y la solución general de la ecuación diferencial parcial de (1) puede ser obtenida. Más adelante ilustraremos esto que hemos mencionado.
Sean las nuevas coordenadas (ξ, η) están relacionadas con las coordenadas (x, y) por las ecuaciones siguientes

Ya que solamente estamos interesados en transformaciones de coordenadas suaves no singulares, necesitamos que las funciones ξ(x, y), η(x, у) sean de clase C1 y que su Jacobiano sea diferente de cero, es decir,
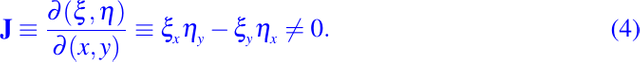
Si la condición (4) se satisface en el punto (x0,y0) de Ω, entonces sabemos que en un entorno de (x0,y0) también tenemos las relaciones inversas dadas por

Ahora de la Regla de la Cadena, tenemos lo siguiente

y sustituyendo las ecuaciones dadas en (5) y (6) en la ecuación (1) obtenemos la siguiente ecuación

donde

De la ecuación dada en (8) vemos que B = 0 si η es solución de la ecuación diferencial parcial de primer orden

La ecuación dada por (9) tiene infinitas soluciones. Podemos encontrar una de estas por asignación del valor inicial en una curva inicial no característica y solucionando el problema de valor inicial resultante de acuerdo con el método descrito en la Lección #5. Supongamos, por ejemplo, que a(x0, y0) es distinto de cero, podemos asignar

Ya que la curva inicial x = x0 no es característica con respecto a (9) en (x0,y0), entonces existe una única solución de (9) - (10) en un entorno U de (x0,y0)
Sea η(x, у) una solución de (9) - (10) en un entorno de (x0,y0). Así, somo libres de elegir la función ξ(x, у) sujeta solo a la condición dada en (4) que J sea distinto de cero. De la ecuación mostrada en (10) tenemos
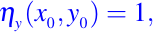
y si elegimos

la condición (4) se satisface en (x0,y0). Por lo tanto, también se satisface en un entorno de (x0,y0). Sea U un entorno de (x0,y0) en el cual η(x, у) esta definida y al mismo tiempo J es distinto de cero. Entonces A es distinto de cero en U. Para A = 0 en algún punto de U, entonces en ese punto la ecuación (8) toma la forma de un sistema de ecuaciones lineales homogéneas y a y b con J precisamente el determinante de esos coeficientes. Ya que J es distinto de cero, tanto a y b se anulan en ese punto, lo cual es una contradicción ya que asumimos que a y b no se anulan simultaneamente.
Finalmente ya que B = 0 y A es distinto de cero en U, podemos dividir la ecuación dada en (7) por A y obtenemos la forma canónica deseada (2). Debemos resaltar que las funciones ξ(x, у) y η(x, у) describen las transformaciones de coordenadas dadas en (3) la cual producen la forma canónica mostrada en (2) podemos elegir de muchas maneras. Sin embrago, ya que η(x, у) satisface la ecuación (9) la curva de nivel η(x, у) = constante, son siempre curvas características de (1). El segundo conjunto de curvas coordenadas ξ(x, у) = constantes se pueden tomar como cualquier familia a un parámetro de curvas suaves las cuales son tangentes a las curvas características, lo cual lo ilustramos en la siguiente figura. Es de hacer notar que este conjunto de curvas coordenadas lo podemos escoger como líneas paralelas al eje y.
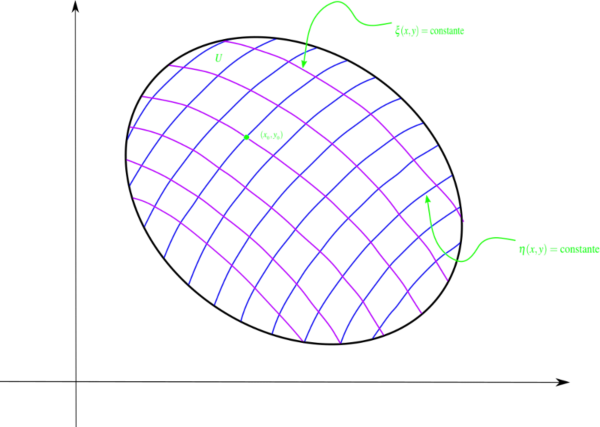
Imagen elaborada con Inkscape, por @abdulmath.

Ejemplo
Sea la ecuación dada por

Como podemos observar, en está ecuación identificamos a = 1, b = x, c = 0 y d = -y y el dominio es Ω = R2. Podemos tomar (x0, y0) = (0,0). La función η satisface la ecuación

y podemos tomar como condición inicial

La solución general de
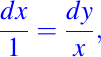
es
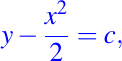
por lo tanto la solución general esta dada por:
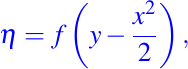
luego, para satisfacer la ecuación dada en (13) debemos tomar f(y) = y y así obtenemos la solución de (12) y (13),

en todo R2. Si tomamos

vemos que el Jacobiano es
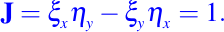
Por lo tanto, (14) y (15) dan la transformación de coordenadas en todo R2 y las relaciones inversas son
Ahora,
y en las nuevas coordanadas (ξ, η) la ecuación diferencial parcial dada por (11) se convierte en

La solución generel de (16) es

donde f(η) es una función arbitraria de η. Devolviendonos a las variables x e y obtenemos la solución general de (11) - (18)


Formas Canonicas, Clasificación de las Ecuaciones Diferenciales Parciales de 2do Orden en dos Variables Independientes
La ecuación diferencial parcial lineal de 2do orden en dos variables independientes es una ecuación de la forma

donde a, b, c, d, e, f, g son funciones de dos variables x, y. Asumiremos que las funciones a, b y c son funciones de clase C2 que no sea anulan de manera simultanea. Estudiaremos la ecuación dada en (19) en dominios Ω subconjuntos de R2en el cual es discriminante dado por:

es ya sea, en todas partes positivo, en todas partes negativo o en todas partes cero, en el dominio Ω. Nosotros mostraremos que para cada punto (x0, y0) de Ω podemos encontar un entorno U contenido en Ω del punto (x0, y0) y nuevas coordenadas ξ y η así que en U y en términos de las nuevas coordenadas la forma de la ecuación (19) es tal que la parte principal es particularmente simple. Entonces decimos que la ecuación esta en su forma canonica en U. Es posible encontrar nuevas coordenadas en todo el dominio Ω tal que en términos de las nuevas coordenadas la ecuación esta en la forma canonica en todo el dominio Ω. Sin embargo, esto requiere suposiciones adicionales en a, b y c, las cuales no detallaremos aquí.
Sea las nuevas coordenadas ξ, η, las cuales están relacionadas con las antiguas coordenadas x, y a traves de las ecuaciones

Ya que solo estamos interesados en transformaciones de coordenadas suaves y no singulares requerimos que las funciones ξ(x, у), η(x, у) sean de clase C2 y que el Jacobiano sea distinto de cero, es decir,
En un entorno de cualquier punto (x0, y0) de Ω donde la condición (22) se satisface tembién tenemos las relacones inversas

Ahora, usando la regla de la cedena tenemos

y
En las ecuaciones dadas en (25) escribimos solamentelos términos que involucran derivadas de segundo orden de u. Sustituyendo las ecuaciones mostradas en (23), (24) y (25) en la ecuación (19) obtenemos la ecuación en la forma de las nuevas coordenadas ξ, η

donde
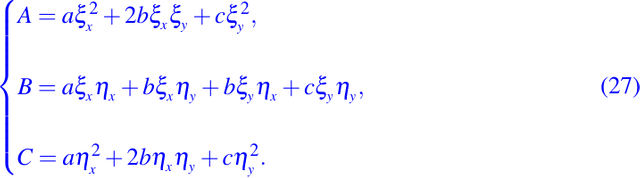
Notemos primero que usando las ecuaciones dadas en (27) podemos probar una relación importante
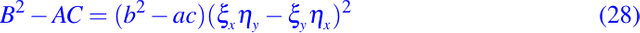
ó

donde
es el discriminante de la ecuación diferencial parcial en las nuevas coordenadas (ξ, η)

En vista de la relación dada en (22), la ecuación dada en (29) muestra que si la transformación de coordenadas es suave y no singular, el signo de el discriminante de la ecuación (19) no cambia. Esto lo enunciamos en el siguiente Teorema.

El teorema nos muestra que si el discriminante es positivo, negativo o cero, es una propiedad intrínseca de la ecuación la cual no depende de el sistema de coordenadas en particular que se use. Esto sugiere que las ecuaciones diferenciales parciales de segundo orden se clasifiquen de acuerdo al signo del discriminante. Veamos la siguiente definición.


Ejemplos
- La ecuación de onda
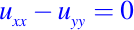
es hiperbólica en R2. - La ecuación del calor
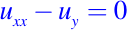
es parabólica en R2. - La ecuación de Laplace
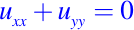
es elíptica en R2. - La ecuación de Tricomi
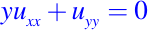
es elíptica en el plano superior y > 0, es parabólica en la línea y = 0 y es hiperbólica en el plano inferior y < 0.

Consideraremos ahora cada tipo de ecuación de segundo orden por separado.

Para una demostración de este teorema, recomendamos al lector consultar algunas de las referencias anexas, o si es de su gusto, un libro que trate el tema de las Ecuaciones Diferenciales Parciales.
Ejemplo (caso hiperbólico)
Consideremos la ecuación de onda siguiente

la cual es hiperbólica en R2. En esta ecuación a = 1, b = 0, c = -1 y por lo tanto la ecuación característica es

la cual tiene las siguientes raíces

Las funciones ξ(x, у) y η(x, у) deben satisfacer las ecuaciones
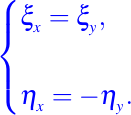
Las funciones
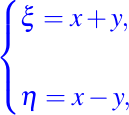
son soluciones de esta ecuación en R2 y el Jacobiano es
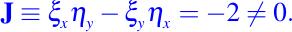
En las coordenadas ξ, η la ecuación de onda tiene la forma canónica

De esta ecuación obtenemos

donde f es una función arbitraria en una variable. Así, de esta otra última ecuación obtenemos

donde F y G son funciones arbitrarias de una variable. La ecuación dada por (36) da la solución general de (34). Devolviendo a las variables iniciales x, y obtenemos la solución general de la ecuación de onda mostrada en (33), como sigue

Para el caso parabólico enunciemos el siguiente teorema

De acuerdo con el Teorema anterior, en un entorno de cualquier punto, al introducir nuevas coordenadas, cualquier ecuación parabólica en dos variables independientes puede ser llevada a una forma canónica teniendo como parte principal la misma que la de la ecuación de calor.
Para una demostración de este teorema, recomendamos al lector consultar algunas de las referencias anexas, o si es de su gusto, un libro que trate el tema de las Ecuaciones Diferenciales Parciales.
Para el caso elíptico enunciemos el siguiente teorema

El teorema 4 nos indica, que en un entorno de cualquier punto, al introducir nuevas coordenadas, cualquier ecuación elíptica en dos variables independientes puede ser llevada a una forma canónica teniendo como forma canónica tiene como parte principal la misma de la ecuación de Laplace.
Para la prueba de este teorema, la cual no escribiremos aquí, es considerablemente de mucha mayor dificultad que las pruebas de los teoremas anteriores. El lector interesado puede revisarla en el libro siguiente
- Garabedian, P. R. Partial Differential Equations, John Wiley & Sons, Inc., New york. 1964.
Si se supone que los coeficientes a, b y c son analíticos, la prueba es más simple e implica la continuación analítica en el dominio de valores complejos de las variables x y у. Es bueno mencionar, que las ecuaciones elípticas no tienen curvas características .

Queridos amigos y lectores, espero hayan disfrutado y aprendido en esta 11va Lección de la serie de Introducción a las Ecuaciones Diferenciales Parciales, de igual manera los invito para la 12va Lección de esta serie, donde continuaremos tratando este tema tan interesante y de mucha aplicación. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias:
- Lang, Serge. Calculus of Several Variables. Springer Science & Business Media, 2012.
- Edwards, Charles Henry. Advanced Calculus of Several Variables. Courier Corporation, 2012.
- Dennemeyer, Rene. Introduction to Partial Differential Equations and Boundary Value Problems. 1968.
- Pinchover, Yehuda, and Jacob Rubinstein. An Introduction to Partial Differential Equations. Cambridge University Press, 2005.
También los invito a leer las anteriores publicaciones de está serie de Introducción a las Ecuaciones Diferenciales Parciales, que estoy seguro serán de su interés:
Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre,  , GIMP e Inkscape.
, GIMP e Inkscape.

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.

Imagen diseñada con GIMP y elaborada por @abdulmath.
Congratulations @abdulmath! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Thanks for the support