Motivación del cálculo diferencial // Aplicación de la derivada a la economía

La derivada dentro del campo de la economía tiene sus aplicaciones dentro del estudio de la derivada vista bajo ese enfoque de tasa de variación.

En economía se ve un fenómeno muy peculiar que encuentra muchas respuesta en la derivada, y es que la variación que tiene una variable con respecto a otra la podemos asociar al concepto de variación promedio, dado que la derivada también estudia los comportamientos de carácter instantáneo, en esta oportunidad me centraré en la variación con características promedios e instantáneas, es decir evaluar el comportamiento del cambio que puede sufrir los costos de producción de determinado artículo, esto es mejor conocido como variación promedio y variación marginal (instantánea).

En ámbitos generales sería muy propicio generar una conceptualización de lo que significa "variación promedio".

Imaginémonos dos variables, una, donde su valor depende de cómo varíe la otra variable, entonces la variación de la variable que está sujeta a cambios está comprendida en un intervalo de valores, en donde los valores que esta tome afecta directamente el valor de la otra variable.

Ejemplo de ello:

^{Autor de la imagen: @carlos84}

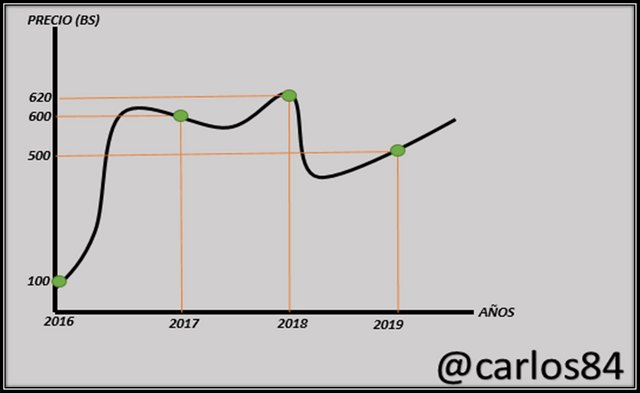
Imaginémonos algún artículo que para el 2016 tiene un precio de 100 Bs, y que ese artículo es sometido a la evaluación de la variación de su precio para los años 2017, 2018 y 2019. En el mismo gráfico podemos ver que determinado artículo tiene un precio de:

• 600 Bs para el 2017
• 620 Bs para el 2018
• 500 Bs para el 2019

Para entender lo de variación promedio podemos analizar dos puntos de la curva, por ejemplo el punto (2017, 600) y (2019, 500), bajo estas condiciones estamos considerando un intervalo entre los años de evaluación de los precios, por lo que la variación que podamos observar de los precios del artículo en este intervalo con respecto al tiempo es lo que podemos denominar costo promedio del artículo.

Una pregunta de análisis concerniente antes de caer en la otra conceptualización es:

¿Bajo qué otra circunstancia puede ser evaluada esta variación?

Alguien pudiera pensar que no quiere evaluar la variación del artículo de su precio con respecto al tiempo en un intervalo, sino que lo quiere evaluar en un instante de tiempo, por ejemplo evaluar la variación del tiempo para el año 2018.

Es aquí donde ocurre el inconveniente ya que para calcular la pendiente de la recta que es tangente a esa curva en el punto (2018, 620) se debe de conocer otro punto, esto con la intención de aplicar la definición del cálculo de pendiente de una recta conociendo dos puntos, dado que solo conocemos uno solo es donde viene a tomar protagonismo la derivada.

^{Autor de la imagen: @carlos84}

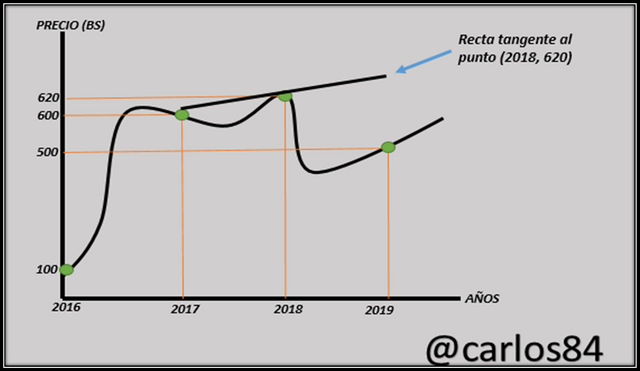
Todo este análisis nos hace reflexionar, sobre que la variación del precio de un artículo con respecto al tiempo en un instante de tiempo (es decir cuando solo se conoce un solo punto) es lo que se conoce como "costo marginal".

Entendidos todas estas premisas, tenemos entonces dos tipos de costos que serán analizados en este artículo que son:

1. Cálculo de costo promedio
2. Cálculo de costo marginal.

Para realizar el cálculo de estos dos tipos de costos quiero partir de la idea, de que no se obtendrá los datos específicos de tiempos y costos asociados, sino que contaremos con una función que la llamaremos función de costo total.

Por ejemplo se puede definir esta función como C(x), asumiendo que C(x) es el costo total para llegar a producir x unidades de un artículo.

La variable x representa la cantidad de unidades de un artículo.

Dado que C(x) es el costo total, se puede definir entonces la función para costo promedio y costo marginal.

El costo promedio: el costo promedio se encuentra al dividir el costo total entre el número de unidades producidas, por lo que si Q(x) es el valor de una moneda fiduciaria del costo promedio, se cumple que:

^{Autor de la imagen: @carlos84}
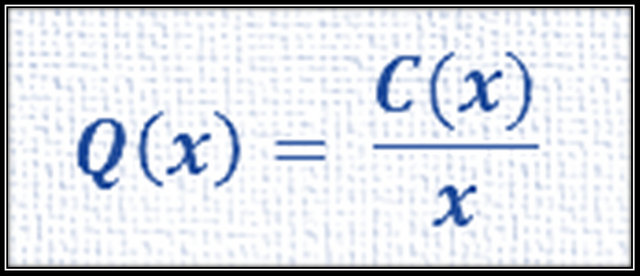
En donde Q es la función de costo promedio.

Bajo estas circunstancias, podemos suponer que originalmente el número de unidades producidas de determinado artículo es la variable x1, y que el incremento de su precio ocurre respecto a ∆𝒙, por lo que la variación del costo total por unidades producidas del artículo está representada por C(𝒙1 + ∆𝒙) - C(𝒙1), por lo que después de todas estas deducciones podemos concluir que la variación promedio en el costo total con respecto a la variación del número de unidades producidas está dado por:

^{Autor de la imagen: @carlos84}

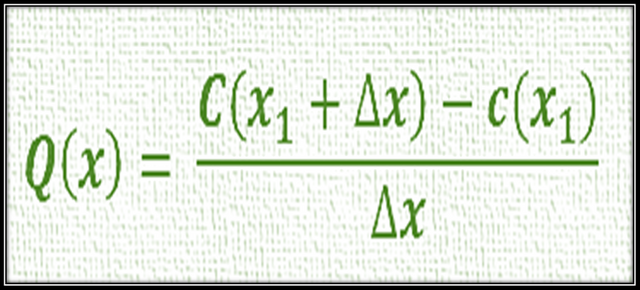
¿Esta ecuación de costo marginal tiene alguna similitud con la de la derivada?

Claro amigos, podemos decir con toda certeza que tiene una igualdad a la ecuación que describe la derivada por definición, y es que los economistas pueden llegar a utilizar este principio para determinar la derivada de la función de costo marginal para determinar la tasa de variación del costo total cuando se producen x1 unidades de un artículo.

Ejemplo

Supóngase la función C(x) medido en Bs como el costo total por la fabricación de x cantidad de tubos de perforación, por lo que la función de costo total se puede expresar tal como sigue:

^{Autor de la imagen: @carlos84}

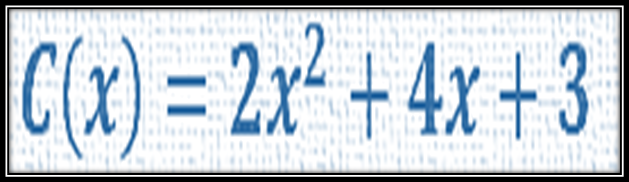
Esta función de costo total por la fabricación de x unidades de tubos de perforación está representada por una parábola tal y como se muestra a continuación:

^{Autor de la imagen: @carlos84}

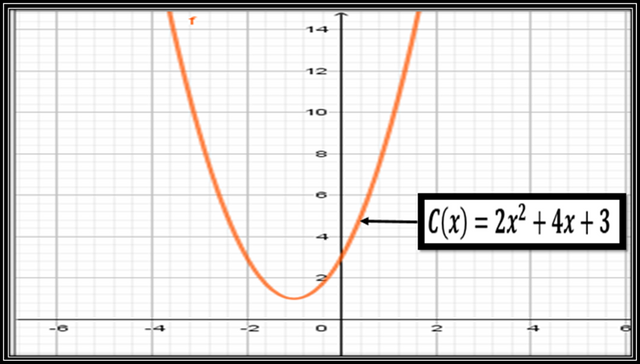
Donde el eje x representa la cantidad de tubos fabricados, y el eje y representa el costo total por la fabricación de x unidades de tubos.

Teniendo en cuenta esta descripción se pide que:

1. Encontrar la función de costo marginal.
2. ¿Cuál es el costo marginal cuando se han fabricado 50 tubos de perforación?
3. ¿Cuál es el precio en Bs del costo real de fabricación del tubo número 51?

Para encontrar la función de costo marginal simplemente tenemos que encontrar la primera derivada de la función de costo total:

^{Autor de la imagen: @carlos84}

Ya obtenida la función de costo marginal, podemos calcular el costo marginal para la producción de x unidades de tubos de perforación, y de esta manera le damos respuesta a la segunda pregunta:

El precio del costo marginal de la producción cuando se han fabricado 50 tubos de perforación, se encuentra sustituyendo el valor de 50 en la función de costo marginal:

^{Autor de la imagen: @carlos84}

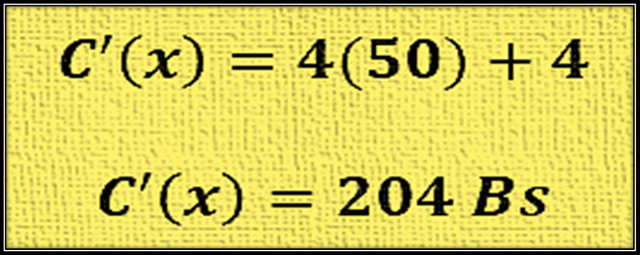
Se puede concluir que, para la tasa de variación del costo total cuando se fabrican 50 tubos de perforación el costo es de 204 Bs por tubo.

Para dar respuesta a la tercera parte, tenemos que tener en cuenta la teoría del costo promedio, es decir debe existir la evaluación en un intervalo determinado, el valor en Bs del costo real de fabricación del tubo de perforación número 51 implica tomar un intervalo que va desde el tubo de perforación número 51 hasta el tubo número 50, por lo que quedaría de la siguiente manera:

^{Autor de la imagen: @carlos84}

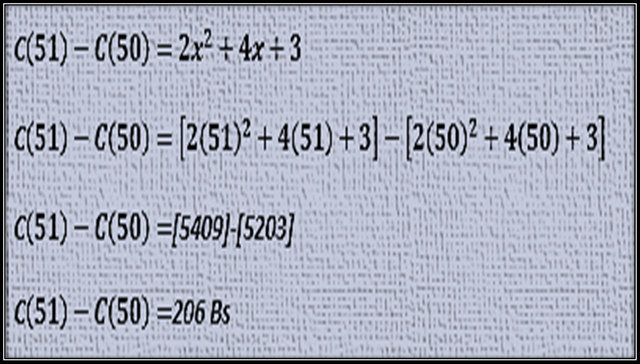
Analicemos un poco, si se observa, se puede notar que los costos marginal de cuando se fabrican 50 tubos, y de cuando se fabrica el tubo 51 es de una diferencia en costo de 2 Bs, esto se debe primordialmente a que el costo marginal es la tasa de variación instantánea de la función del costo total con respecto a una variación de unidad de tubos fabricados.

También para los economistas resulta más útil aproximar el costo de producción de una unidad adicional empleando la función de costo marginal.

Saludos amigos, esperando que sea del gusto y agrado de todos, hasta una próxima entrega.

Nota: Todas las imágenes son de mi autoría, y fueron elaboradas empleando las herramientas de imagen de Microsoft Power Point. La imagen donde se grafica la función parabólica es apoyada mediante el uso del software geogebra 5.0

Bibliografía consultada

Libro de Cálculo con Geometría Análitica. Autor: Leithold. 7ma edición.