How Did They Measure The Height of the Everest Mountain 162 Years Ago?
Do you know Colonel Sir George Everest? You may probably not have heard of him, but I bet you find his last name fascinating. Does it ring a bell? I bet it does. Who has not heard of the highest mountain above sea level on earth which goes by the name of Mount Everest?
Now we are getting somewhere.
But just in case you did not know, now is a great time to catch up. The man, Sir George Everest is a British surveyor, and geographer and the highest mountain is then known as Peak XV was renamed in his honour.
George Everest was then the Surveyor General of India. The man that did the measurement was an Indian mathematician, Radhanath Sikdar, who was employed as a "computer", in the Great Trigonometrical Survey where Sir George Everest was the superintendent between 1823-1843. The people who do maths calculation during the early 17th Century up till the end of the 20th century are known as the human computers.
In 1852, Radhanath Sikdar announced to the world that the Peak XV (now Mount Everest) is the highest mountain above sea level at the height of 29,000 feet (8,839.2m). Though the announcers added 2 feet to make it more believable
Waugh concluded that Peak XV was "most probably the highest in the world".Peak XV (measured in feet) ... to be exactly 29,000 ft (8,839.2 m) high, but was publicly declared to be 29,002 ft (8,839.8 m) in order to avoid the impression that an exact height of 29,000 feet (8,839.2 m) was nothing more than a rounded estimate. Waugh is sometimes playfully credited with being "the first person to put two feet on top of Mount Everest".Wikipedia.
The official height of Mount Everest established nearly a century later in 1955 by the Indian survey is 8,848m (29,029 ft). In 1999, a team from the USA armed with the latest technology of GPS were able to measure the mountain to be 29,035 ft which merely is 33 feet off from the last century's measurement! How did the 19th-century surveyors get this accurate?
As a kid, we all use to measure our height with the 12-inch mathematics set ruler. Estimating a 29,035 feet mountain with such is not impossible, but you may agree it will take an awful time and incredible energy to pull that off.
But here we are with a result so accurate we are left to wonder how the surveyors pulled it off 162 years ago in 1856.
How they did it
The answer is staring us in the face all along. It is one word: mathematics. Or more specifically trigonometry.
The Everest team employed the help of trigonometry which involves less sophisticated instruments such as that obtainable by the modern day use of GPS. The triangles, similar to that of the principle of GPS, is what the Victorian surveyors used to measure tall structures before the technology of satellite was around.
If we want to calculate the height of an unknown tall object, a tree, like in this example. Let us assume we are 20 feet away from the base of the tree and our height is 5 feet. The unknown height of the tree is T.
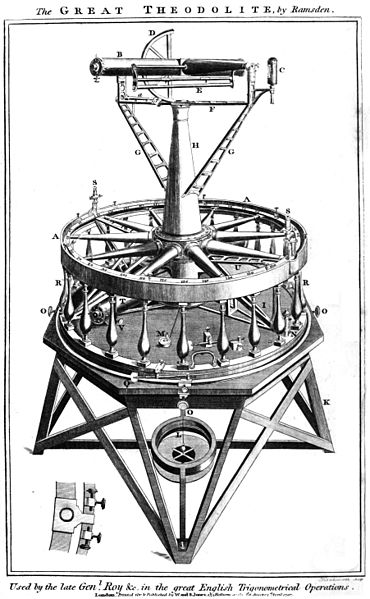
The theodolite is similar to an advanced protractor. It is used in the measurement of the angles of elevation (like the 38° angle in the above example) and depression.
To calculate the height of the tree, T we shall use the trigonometry.
Tan of an angle= opposite ÷ adjacent
Tan (38°) = opposite ÷adjacent = T÷20
Tan (38°) =T/20
T= 20 tan (38°)
=20 * 0.7812 = 15.6257
Adding the height of the observer
Total height of the tree, T= 15.657+ 5= 20.6257 ≈ 20.63 feet
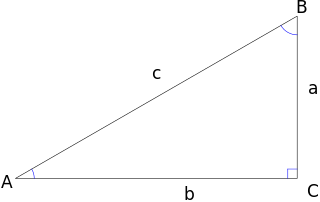
If the a= height of the unknown mountain, with angles at A (where the observer is) and B measured by a theodolite.
Assuming angle at A= 30°
and the angle at B= 60°
Remembering the trigonometric ratios:
Cos 30°= adjacent/ hypotenus=b/c
Cos 60°= a/c
Cos 30°/Cos 60°= (b/c) ÷ (a/c) = b/c x c/a, the cs will cancel out to leave b/a
Cos 30°/Cos 60°= b/a
The distance, b, is already measured by the surveyors that are some distance from the base of the mountain to where the surveyors mounted their theodolite (which is A).
The value of a, which is the height of the mountain can then be determined.
To further remove any errors, different measurements of locations for A is calculated. By using different triangles, the member of the Great Trigonometrical Survey was able to figure the height of the mountain to be 29,000 feet. Funny enough they had to add 2 feet to make it look more authenticate rather than guesswork, a move which actually made their measurement more accurate as a modern method of elevation measurement showed.
Those guys deserve a lot more recognition for their astounding work with mathematics.
Now do you still hate all those math at high school?
See how awesome someone can apply it in real-life situations.
I will like to see where, if any, there is a situation where your maths skill saved the day or help you carry out a project in real life situation.
REFERENCES
- Wikipedia: Mount Everest
- Wikipedia:George Everest
- Mount Everest: named after the first surveyor general of India
- 29,000 feet exactly? Nah, Shove Another 2 Feet on There
- New project could finally answer mystery of Mt. Everest's height
- 7 Things You Should Know About Mount Everest
- Shrinking Mount Everest: How to Measure a Mountain


I never really thought of this, this is pretty insightful. All I can remember is that Mountain Everest is the tallest mountain. I never really gave thought to how it came to be that. This is useful, thank you.
Thank you. Some things are easily overlooked.
This post was upvoted by Steemgridcoin with the aim of promoting discussions surrounding Gridcoin and science.
This service is free. You can learn more on how to help here.
Have a nice day. :)
I like anyone that promotes science and/or discussion on steemit. Thank you.
Barometers were also used to measure the heights of mountains, simply by calculating air pressure. They were a lot less reliable than theodolites, however.
I think it works on the same principle that the pressure altimeter used in aircraft uses to determine heights from ground.
Sounds about right!
Being A SteemStem Member
Thank you.