Exploring The Universe With LHC
How can LHC test astrophysics phenomena? How is relativity used to calculate collisions at LHC? Are you better than a computer at finding the Higgs boson? We answer all of this, and much more in this interactive experience.
For the optimal experience, and for all interactive elements to work, read the series on kasperfred.com
Introduction

This project is an interactive experience consisting of a series of interlinked webpages which contain text, pictures, equations, videos, and other interactive elements to explore the topic: Exploring the universe with LHC.
For the best experience, we recommend using the latest version of Chrome desktop with Javascript and cookies enabled.
Along the way, you can refer to the interactive glossary for terms and theorems.
To each page, there's an associated public discussion thread which meant to provide an outlet for any questions or comments the reader might have while exploring the interactive experience.
You can access this thread by clicking on the blue "discuss" button at the top of any article.
Glossary

To access the glossary, read the series on kasperfred.com
What is LHC:ATLAS?
Accelerating particles close to the speed of light and colliding them hoping something interesting will happen.
LHC
The Large Hadron Collider (LHC) is the result of a multinational collaboration with over 10,000 scientists and 100 countries.
By colliding charged particles, mostly protons, at speeds close to that of the speed of light, the LHC has made discoveries ranging from the confirmation of the existence and properties of the Higgs boson, to the likely non-existence of supersymmetrical particles and, recently, the discovery of two baryons composed of one bottom quark and two up quarks, and one bottom quark and two down quarks.
ATLAS

A picture of the caliometers of the ATLAS detector.
ATLAS is one of the four main detectors at LHC, and measures the decay products from the collisions. When protons hit head on in inelastic relativistic collisions, they create new particles which spread around in the detector. The atlas detector is constructed as a cylinder with multiple layers. The different layers can measure different properties of the decay products.
ATLAS Structure
The ATLAS detector is constructed as a cylinder through which the particle beams shoot. Upon a head-on collision, the protons decay to other particles which scatter in all directions. This is possible while conserving momentum precisely because the protons collided head on.
Since we cannot predict where the decay go, the detectors are constructed as approximate onion-like shells around the beam direction as illustrated below.
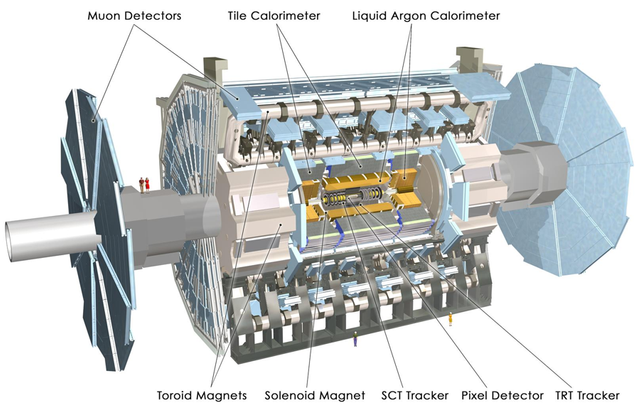
Schematic of ATLAS from Kjende@CERN
In the innermost shell, we have tracking devices such as the Xenon gas tubes, which can track as charged particles go through them, and the PIXEL/SCT trackers. Which is explained well in the following video:
To see the video, read the article on kasperfred.com
Knowing the trajectory of the particles along with strong magnets which curve the trajectory allows us, with some difficulty when dealing with multiple particles, to calculate the relativistic momentum of the charged particles.
In the next shell, the particles pass through calorimeters which tries to measure the energy of the particles by absorbing them passively through high density materials such as lead, and actively through liquid argon for example.
Electromagnetic and Hadronic calorimeters can stop most particles, but neutrinos and muons.
The next shells detects Cherenkov and transition radiation, and at the outermost shell, we have the the muon spectrometers.
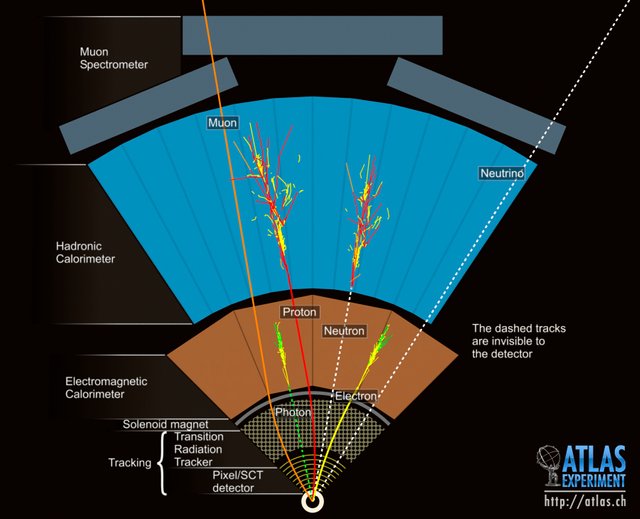
On the picture above, we see the inner shells where the trackers can see the charged particles such as the proton, electron and muon. Notice, how the magnets bend the paths of the particles.
In the calorimeters, we see most particles being absorbed and decay to other particles. By observing the decay particles, and considering quantum symmetries, we can figure out the types of decay particles as has been colored in on the image.
Notice further that we cannot directly detect neutrinos in the detector. Instead, we have to rely on inference from looking at the missing total energy in the system because we know there's conservation of energy even if some of it goes to creating new particles.
Listen to collisions detected by ATLAS
You can listen to the audio of detected collisions from ATLAS courtesy of Ewan Hill below.
To listen to the collisions, read the article on kasperfred.com
The audio is generated by associating the values from different detectors of a subset of the collisions with MIDI tones and normalizing the frequencies to be within the audible range. 30 seconds is approximately equivalent to one event.
What is Special Relativity?
Time and space are the same thing, and it's all relative?
When we read What is LHC:ATLAS?, I mentioned that since the speed of the particles approaches the speed of light, we have to account for the relativistic effects.
"However, we do have Galilean relativity which has worked perfectly fine for me" you might inject, and you'd be right. Galilean relativity serves us just well in most of our lives. In fact, for speeds far below the speed of light Einstein relativity and Galilean relativity are nearly indistinguishable from each other.
However, in certain circumstances such as when you're using a particle accelerator, or even something as mundane as using GPS, Galilean relativity is not enough, and you have to use Einstein's relativity.
"Okay, so I need this Einstein's relativity. What is it?" you ask begrudgingly.
Einstein's special relativity (refered to just as special relativity from here) can be derived entirely from two fundamental postulates.
The Fundamental Postulates
- All intertial reference frames are equivalent.
This version of the postulate, however, follows a somewhat circular argument as an object which does not accelerate does not have a net force, however, the only way we know that it doesn't have a net force is by checking if the object accelerates.
This inconsistency lead Einstein to develop his general theory of relativity which solves the problem by working for any reference system, and not just inertial systems. However, if you ignore this detail, you'll be fine.
- The speed of light in vacuum, $c$, is a universal constant in all reference frames.
While today, we know this to be true as we have measured it empirically, Einstein couldn't possibly have known this at his time, you rebut. And you'd be right. In fact, it's possible to derive that given that light is a electromagnetic wave that light must travel at $c$ from Maxwell's equations. However, Einstein describes in his notes from 1949 himself finding it as a solution to an apparent paradox he stumbled upon when he was 16. This approach leads to the stronger claim that $c$ is constant in all reference frames.
Notation
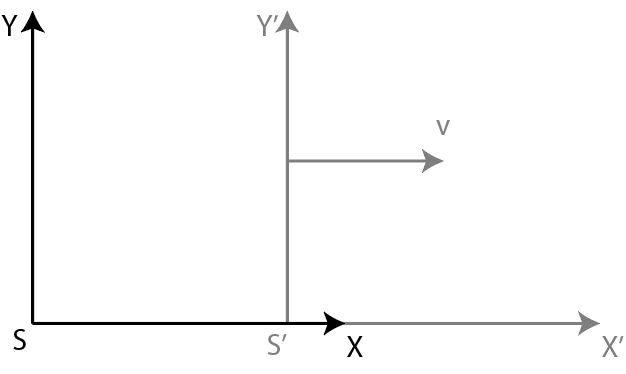
Standard Configuration
The standard configuration is a configuration of coordinate systems often used in special relativity to ease, and somewhat normalize the notation.
The standard configuration consists of an rest system $S$ with coordinates $(x,y)$, and another system $S'$ with coordinates $(x',y')$ moving with $v$ along the $x$-axis with respect to $S$. Furthermore, at $t=0$, we set $x=x'=0$.
This setup is illustrated below.
Four vectors
Since handling the individual dimensions separately can quickly become a mess, it's an often used convention to combine the $3+1$ dimensions into a four vector with the unit vectors:
$$\textbf{e}_t,\textbf{e}_x,\textbf{e}_y,\textbf{e}_z$$
The index of the time dimension can wary between authors. One convention is to use the zeroth dimension as the time dimension, so the unit vectors become
$$\textbf{e}_0,\textbf{e}_1,\textbf{e}_2,\textbf{e}_3$$
which gives us the four vector
$$\textbf{a}=\sum_{a=0}^3 a^\alpha \textbf{e}_\alpha.$$
By using Einstein notation, we get
$$\textbf{a}=a^\alpha \textbf{e}_\alpha$$
where it's assumed we sum over repeated greek letters.
We have adopted the convention where we denote four vectors with bold face such as, $\textbf{a}$, while we continue to denote three vectors with an arrow such as, $\vec{a}$.
For some more syntatic sugar, let
$$\eta_{\alpha \beta} = \textbf{e}\alpha \cdot \textbf{e}\beta =
\begin{bmatrix}
-1&0&0&0\
0&1&0&0\
0&0&1&0\
0&0&0&1
\end{bmatrix}.$$
In which case
$$\textbf{a}\cdot \textbf{b}=\eta_{\alpha \beta} a^\alpha b^\beta.$$
The reason we have a $-1$, and not $1$ in the time dimension is to avoid messing up causality which the philosophers tell me is a good thing.
One neat thing about using four vectors is that the dot product between any two four vectors (or a chain of them) is invariant. So
$$\textbf{a} \cdot \textbf{b} = \textbf{a}' \cdot \textbf{b}' .$$
Lorentz Transformation
In the standard configuration, the componentwise Lorentz transformation is given by
$$
\begin{aligned}
&a'^{0} = \gamma(a^{0} - \beta a^1 ), \
&a'^{1} = \gamma(a^{1} - \beta a^0 ), \
&a'^{2} = a^2, \
&a'^{3} = a^3. \
\end{aligned}
$$
Time Contraction
While deriving every formula of special relativity is beyond the scope of this project, deriving time contraction seems worthwhile due to it's broad applicability.
To see the video read the article on kasperfred.com
Let's consider a light-clock consisting of two perfect mirrors put parallel with a distance $L$ to each other, and let a foton travelling at speed $c$ bounce between the mirrors.
Obviously, the time it takes for the foton to bounce from the bottom mirror to the top mirror and back again is going to be
$$ t = \frac{2L}{c}$$
because time equals distance over speed.
This can be rewritten as
$$ L = \frac{ct}{2} $$
Now, let's consider the same system, but this time the mirrors move along the $x$-axis with velocity $v$ while the foton continous to bounce between the mirrors.
Let the time it takes for the foton to complete one full bounce be $t'$, and let the distance the mirrors have moved before the foton comes back be $2s$. Then we know that
$$ 2s = v\cdot t'.$$
So we can write $s=\frac{v\cdot t'}{2}$.
We know that the foton travels along $h$ twice for a total distance of $2h$, so we find that
$$2h=c\cdot t.$$
We now have all the sides in a right-angled triangled, and per pythagoras, we know that
$$
\big(\frac{vt'}{2}\big)^2 + \big(\frac{ct}{2}\big)^2 = \big(\frac{ct'}{2}\big)^2.
$$
Which gives us
$$
c^2t^2 = c^2 t'^2 - v^2t'^2.
$$
By dividing by $c^2$, we find
$$
t^2 = t'^2 - \frac{v^2t'^2}{c^2}=t'^2 \big( 1 - \frac{v^2}{c^2} \big).
$$
Isolating $t'$, we find
$$
t' = t \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}.
$$
Or when $\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$,
$$t' = t \gamma. $$
Relativistic Mechanics
Just like classcal mechanics, we still have conservation of momemtum and total energy in relativistic collisions.
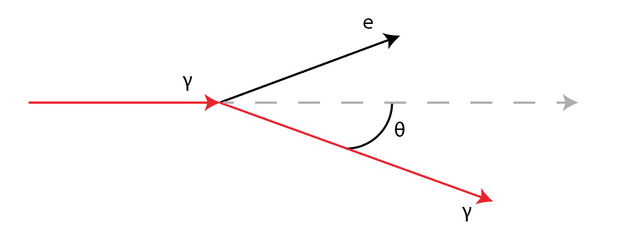
Example: Compton Spread
We consider a system consisting of a photon and an electron. In the initial state, the photon has a four momentum vector $\textbf{p}_\gamma$, and the electron is at rest, $\textbf{p}_e = m_e c(1,\vec{0})$.
In the final state, the photon has the four momentum vector $\bar{\textbf{p}}_\gamma$, and the electron has the four momentum vector $\bar{\textbf{p}}_e$.
The setup is illustrated below.
This is an example of Compton spread. The angle of spreading $\theta$ depends on the wavelength of the incoming photon with the relation
$$\bar{\lambda}=\lambda+\lambda_c(1-\cos(\theta))$$
where $\lambda_c = \frac{h}{m_e c}$.
The Higgs
Catchy subtitle is not needed
The confirmation of the existence of the Higgs boson is probably one of the most important findings made by the LHC. Not only did it complete the Standard model, but also gave insight into the early cosmological universe by having a better understanding of how the processes could function.
So not only does the LHC play an important role in furthering particle physics, but its findings are of high significance for astrophysicists who seek to understand the early universe some of whose properties are best emulated in a particle accelerator.
Finding the Higgs
Finding the Higgs boson is not easy. Not only does it decay about an order of magnitude faster than other elementary particles making it impossible to detect directly in ATLAS, or other detectors, while it does decay into a lot of things, all of those are very common making isolating the Higgs boson very difficult.
One common decay pattern is for the Higgs boson to decay to two photons ($H\rightarrow \gamma_1 \gamma_2$) with the 4 momntum vectors $\textbf{p}^\alpha_{\gamma_1}= \frac{E_1}{c} \cdot (1,\hat{n}1)$ and $\textbf{p}^\alpha{\gamma_2}= \frac{E_2}{c} \cdot (2,\hat{n}_2)$. Furthermore, we know the angle between the two photon beams is given by $\theta$, and $\cos(\theta)=\hat{n}_1\cdot\hat{n}_2$.
Since $\textbf{p}^2=-m_0^2c^2$, and photons don't have a invariant mass, we know that $\textbf{p}_1^2 = \textbf{p}_2^2 = 0$.
We therefore find that $(\textbf{p}^\alpha_{\gamma_1}+\textbf{p}^\alpha_{\gamma_2})^2=2\textbf{p}^\alpha_{\gamma_1}\cdot\textbf{p}^\alpha_{\gamma_2}$ which gives us
$$(\textbf{p}^\alpha_{\gamma_1}+\textbf{p}^\alpha_{\gamma_2})^2=-2 \frac{E_1E_2}{c^2} (1-cos(\theta)).$$
Remembering that $\textbf{p}^2=-m_0^2c^2$, we can find the invariant mass of the parent particle (the Higgs boson)
$$m_H = \frac{1}{c^2} \sqrt{2E_1E_2(1-\cos(\theta))}.$$
Since $E_1,E_2,\theta$ are all measureable by the detector, we can therefore get a value of the mass of the Higgs boson. Exactly this was done on data from 2011 and 2012 where it was found that the mass of the Higgs boson was around $m_H=126.8 \text{GeV}$.
While the above algebra may seem easy, it's not quite as simple to isolate $H\rightarrow \gamma \gamma$ events. In order to find such events a likelihood function must be developed based on statistical knowledge as well as the physical understanding of the problem. It took most of the first run of the LHC to tune to likelihood function, due to the many tunable parameters, and it's still limiting how many collisions are possible in each batch due to the added noise of more collisions.
These are some of the reasons why experiments in using machine learning algoirthms such as neural networks to let computer automatically find an optimal likelihood function have begun.
Below has a simple neural network been implemented to classify Higgs decay based on the Higgs ML dataset from 2014.
You can use the two features to compete against the neural network in detecting Higgs decays. (The feature values have been normalised, and the $y$-axis is a kernel density estimation of the value. The features have been crafted and chosen from the detector data as those with the highest predictive power)
To play the game, please read the article on kasperfred.com
You can learn more about a similar network to the one above here, or you can learn more about neural networks in general here.


Congratulations @kasperfred! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Do not miss the last post from @steemitboard: