Where Physics and Mathematics Meet

sinbad989 (52)in #mathematics • 6 years ago (edited)

How can it be that mathematics, being after all a product of human thought which is independent of experience, is so admirably appropriate to the objects of reality? ~ Albert Einstein, in Geometry and Experience (1921)

I'm done reading chapter two of the GIAM book, covering some concepts of proof techniques. It was fun and I learn so much from it. I even got some new ideas along the way.

Direct proof, proof by contradiction, proof by cases, proof by contraposition, proof by exhaustion, and proof of existence and uniqueness - I've encountered all of these techniques during my undergraduate without actually knowing they have names. (e.g. prove that this is hermitian, show that Stokes theorem is this, prove that this commutes, prove that this wave function is unique, show that Green's function is that, derive the conservation of energy from this gradient of a potential, etc)

What we've been doing all along, in our daily exercises, proving some equations is actually the heart of mathematics. Proving is not really the main thing that we do in physics, modeling is our main work.

The way I understand how physics work is that we try to boil down phenomena into a minimum number of properties, characterized by simple variables, and create some equations that will describe how it evolves over time and space.

Why am I studying mathematics then? First, it is a fun domain of knowledge. Second, because I've realized that as I go deeper into higher physics, e.g. particle physics, quantum field theory, general relativity, quantum electrodynamics, it becomes more mathematical and abstract. It seems logical to not only obtain a good physical standpoint of a problem but also an extensive mathematical perspective.

Physical Standpoint

Physics is a way of mapping physical phenomena into an understandable system of equations. Its ultimate goal is to understand the inner workings of nature. It always starts with understanding the physical properties and behavior of a phenomenon without concerning too much on the mathematical underpinning.

The trajectory of a ball, characterized by its mass, as it falls is modeled using Newton's law given by the simple but powerful F=ma. Newton did not derive this from some fundamental mathematics theorem but was modeled based on observations or empirical results.

The same line of thinking happened in quantum mechanics - given the potential of a quantum system, one can use an equation called Schrodinger equation to predict the dynamics and extract information from the system. The idea of where these Schrodinger equations came from or how they were derived is not much of a concern in physics. The important thing is it works and its result matches with experiments.

In the field of quantum electrodynamics, it was found that perturbative calculations of some of the integrals were divergent (a fancy term for infinite value ). Scientist developed a technique called renormalization to tame infinity. Renormalization was developed from a physical standpoint. An Infinite result is not allowed in the physical world.

There are, however, results in the physical world that are interesting in the pure mathematical sense.

Mathematical standpoint

I remember, when I was still an undergraduate student, I had a folder (a physical folder) that contains some Clay Institute problems. One of those is the famous Navier–Stokes equations.

In physics, the Navier–Stokes equations /nævˈjeɪ stoʊks/, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of viscous fluid substances. [...] Navier–Stokes equations are useful because they describe the physics of many phenomena of scientific and engineering interest.

The Navier–Stokes equation is one of the seven most important open problems in mathematics. We do not have a full understanding of the solution of the Navier-Stokes equation yet, we do not know if the solution of N-S equations in three dimensions always exist and, if they exist, if they are smooth. More formally, it is known as the Navier–Stokes existence and smoothness problem.

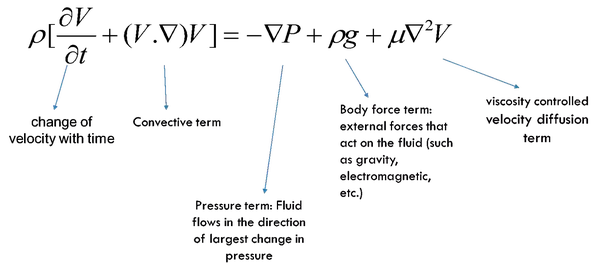
Navier-Stoke equation
In 2010, I remember a Filipino physicist, Amador Muriel of UP Los Banos, was said to have found an exact solution to the problem. In the abstract it says,

An improved operator formalism, heretofore unexplored, is used for uniform initial data. We then choose a Gaussian pair potential between particles. With these two conditions, the velocity fields, energy, and pressure are calculated exactly. All stipulations of the Clay Mathematics Institute for proposed solutions of the 3-D Navier-Stokes Equation are satisfied by our time evolution equation solution.

Sadly, it was not the solution the Clay Institute was looking for. Until now the problem is still open to everyone to poke.

This kind of problems is the kind of problem that led me to deeply consider studying mathematics in my spare time. In the official problem description written by C. L. Fefferman, they ask for a proof of one of the following statements.

Note, they are just looking for one proof of any of the four problems. It sounds simple to me. But if one delves into the mathematical jargons of the problem it becomes unmanageable (in my limited perspective).

I am still far from fully understanding the problem. As of now, I can apply a little technique from what I've learned in logical equivalence, for example:

Instead of looking for the existence and smoothness, we can rephrase the problem and look for a disproof. What if we start from the assumption that there is no physically reasonable solution that exists. What is its implication to NS?

These are raw ideas I got as I was reading the book of J. Fields in the gentle introduction of mathematics. I know I'm far from solving the NS problem, but it feels good that I'm moving infinitesimally forward.

Convergence

As physics is a tool for engineers, mathematics is a tool for physicists. Mathematics and physics have long been in an intimate relationship even at the times of the Greeks. We need it now more than ever as the mathematical models we got from describing physical phenomena becomes more sophisticated. The relationship can be described as follows,