A Gentle Introduction To Mathematics - Two-column Proof
Hello smart steemit readers!!
Yesterday, we've encountered laws concerning logical equivalence. But what are they for? Today, we're going to use them to prove logical equivalence. To do this, we have to be familiar with two-column proof.
This is a grossly, oversimplified example of a two-column proof,
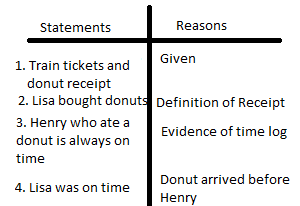
What exactly is a two-column proof?
In the left column, you show your work, being careful to go one step at a time. In the right column, you provide a justification for each step.[1] Simple as that. We've been doing this since elementary, I guess.
We will be going to some examples in two-column proofs in the context of proving logical equivalences. Without further ado, let’s provide a proof of the equivalence:
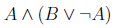
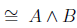
It is given by the following table,
| Logical Equivalence | ||
|---|---|---|
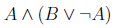 | 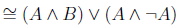 | Distributive law |
 | Complementarity | |
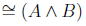 | Identity |
Let’s look at another equivalence:
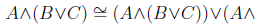
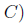
Our first step here is to find a proof that uses the least number of steps, so we need to be careful in choosing the side on which we have to prove. For this case, we’ll start with the right-hand side of this one.
| Logical Equivalence | ||
|---|---|---|
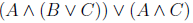 | 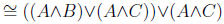 | Distributive law |
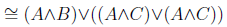 | Associative law | |
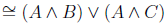 | Distributive law | |
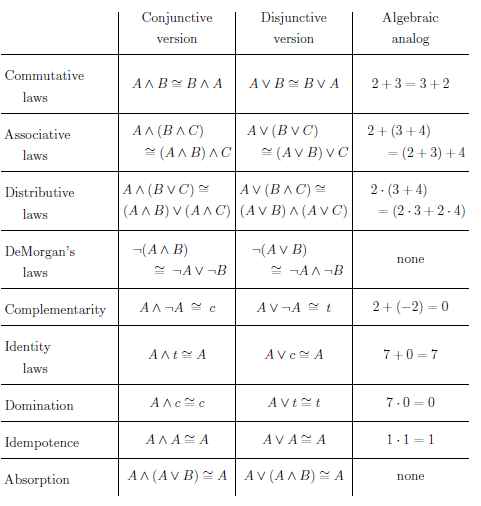
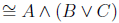 | idempotence |
What we've achieved
We have assembled a nice, step-by-step sequence of equivalences – each justified by a known law - that begins with the left-hand side of the statement to be proved and ends with the right-hand side. That’s an irrefutable proof! [1]
As a last advice in doing two-proof columns,
always start with the more complicated side of the equivalence to be proved. In is more intuitive to work in the direction of making things simpler, but there are times when one has to take one step back before proceeding two steps forward.
always refer to this table to trace back what rule to use to prove a step
Exercise
If you're bored you can solve some of this exercise:
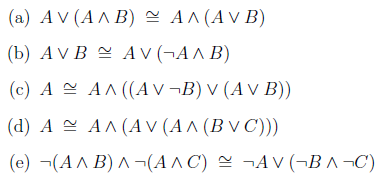
The solution of letter (a) should look like this:
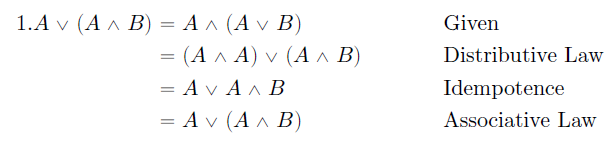
Previous topics you may want to read:
- A Gentle Introduction To Mathematics - Algorithms
- A Gentle Introduction To Mathematics - Relations
- A Gentle Introduction To Mathematics - Predicates and Logical Connectives
- A Gentle Introduction To Mathematics - Implications
- A Gentle Introduction To Mathematics - Logical Equivalence


good post .. this is so a learning resource for me