A Gentle Introduction To Mathematics - The principle of Mathematical Induction
The Principle of Mathematical Induction (PMI) may be the least intuitive proof method available to us. Despite the indisputable fact that proofs by PMI often feels like magic, we need to convince you of the validity of this proof technique. It is one of the most important tools in your mathematical kit!
Axiomatic
The simplest argument in favor of the validity of PMI is simply that it is axiomatic.
The axioms for the natural number system, known as the Peano axioms, include one that justifies PMI.
Domino Toppling
source: sequence of topling dominoes
This is the model one should keep in mind when thinking about PMI: domino toppling. Every domino must be placed so that it will hit and topple its successor. The other thing that has to happen is for someone to knock over the first domino.
Basis and Inductive Steps
Let’s recast our discussion in terms of infinite families of logical statements. If we have a sequence of statements,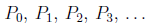 
(one for each natural number) we can prove them all to be true using PMI.
We have to do two things:
- We must show that P(0) is true. (this is usually the easy part)
- We must show, for every possible value of k, P(k) => P(k+1) (i.e. each domino will knock down its successor)
These two parts of an inductive proof are known, respectively as the basis and the inductive step.
An outline of proving statements using PMI:
REALLY IMPORTANT!
When doing the second part of an inductive proof (the inductive step), you are proving a UCS, and if you recall how that’s done, you start by assuming the antecedent is true.
The particular UCS we’ll be dealing with is:
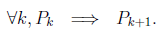
This means that in the course of proving the sentence,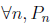 
we have to assume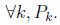 
This is not an error (“circular reasoning”). Note the difference,
is the sentence we’re trying to prove
is the sentence known as the inductive hypothesis
Example: The Size of a Power Set
In section 4.1 we discuss power set. There is a relationship between the size of a set A and its power set P(A). If |A| = n then |P(A)| = 2^n.
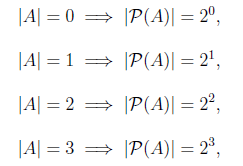
etcetera
Now, let’s apply the two steps we’ve learned.
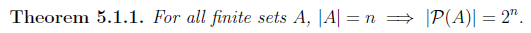
In our basis we must show that P(0) is true:
Q.E.D
Disclaimer: this is a summary of section 5.1 from the book A Gentle Introduction to the Art of Mathematics: by Joe Fields, the content apart from rephrasing is identical, most of the equations are screenshots of the book and the same examples are treated.
