A Gentle Introduction To Mathematics - Direct Proofs of Universal Statements
Direct Proofs of Universal Statements
Previously, we've covered a lot of logic and quantifiers. But we haven't seen their powers yet. Today, we're going to explore proofs, in particular, direct proofs on universal statements.
Disclaimer: this is a summary of section 3.1 from the book A Gentle Introduction to the Art of Mathematics: by Joe Fields, the content apart from rephrasing is identical,most of the equations are screenshots of the book and the same examples are treated.
Fun fact: if you form the product of 4 consecutive numbers, the result will be one less than a perfect square.
No matter have many examples we produce, we haven’t proved the statement – we’ve just given evidence.[1]
How do you prove a universal statement?
The first thing to do in proving a universal statement is to rephrase it as a conditional. The resulting statement is a universal conditional statement or UCS. This makes our hypotheses clearer. For our fun fact example, we can restate it as,
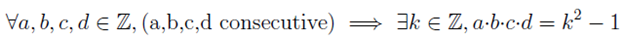
The antecedent of the UCS is that a,b,c, and d must be consecutive. Here’s another important realization – we don’t actually need 4 variables since they are consecutive, a uniquely determines the other three. Finally, we can have a refined version of our statement that we’d like to prove:
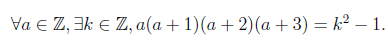
Source
The only thing we need to do now is to come up with a value for k given that we know what a is: a proof of this statement requires some algebra.
Note that,
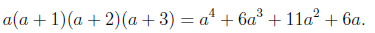
Source
Then, by some form of magic, we have
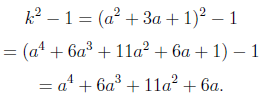
Source
Q.E.D!! We have proven our statement.
Once proof are given, the reason for a statement becomes obvious. However, the source of the proof is sometimes beyond human's normal imagination.
There is a huge difference between devising a proof and writing one. A good proof can be somewhat akin to a good demonstration of magic, a magician doesn’t reveal the inner workings of his trick, neither should a mathematician feel guilty about leaving out some of the details behind the work. [1]
Let's digress a little bit. You might find this technique useful in the future.
A device for doing polynomial arithmetic
For this polynomial, let's create a simple system to get the product
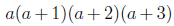
- Multiply each pair, if it is consist of even components. For our case, we have:
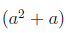 and
and 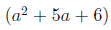
- Create a table that has the terms of these two polynomials as its row and column headings
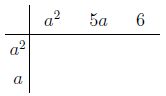
Source - Fill in the entries of the table by multiplying the corresponding row and column headers
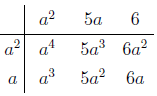
Source - Lastly, add up all the entries of the table, combining any like terms.
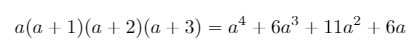
Let’s go back to doing proofs!
We’re going to prove concepts we’ve encountered in the previous posts especially those involving the concepts of elementary number theory. Our goal in this post is to conceive direct proof of universal statements. The thing is, universal statements comes in two flavors – those that appear to involve conditionals, and those that don’t.
A direct proof of a UCS always follows a form known as “generalizing from the generic particular”. We are trying to prove that,
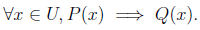
Source
The skeletal outline of the arguments flows like this:

Source
All those dot-dot-dots in the middle are where all the real work is inserted.
Filling those dots will sometimes (rarely) be obvious; more often it will be extremely challenging; it will require great creativity, loads of concentration, you’ll call on your previous mathematical experiences, and you will most likely experience a certain degree of anguish. [1]
Floor of a real number
Remember the following expression from the previous post:
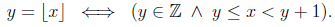
Source
The brackets used to symbolize the floor function is similar to ordinary parentheses that it may seem natural to propose that,
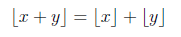
Source
It is wrong. One simple counterexample to this rules is the following: floor(5.9 + 3.1) is not equal to the summation of the individual floor function of 5.9 and 3.1.
Surprisingly, if one of the numbers is an integer, then the intuitive rule works:
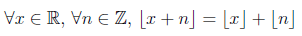
Source
For instance, if you have x=3.1 and n=4, then the floor(7.1) = floor(3.1) + floor(4).
Let’s try to express this as a universal conditional statement: if x is a real number and n is an integer, then
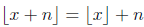
Source
The next most useful ally in constructing proofs are the definitions of the concepts involved. In addition, we’re going to use what we learn on two-column proof. Consider the following,

These definitions are our only available tools so we’ll certainly have to make use of them, and it’s important to notice that that is a good thing. Putting the proof of this statement is nothing but an exercise of utilizing definitions. It is also a testament to the power of naming things.

Finally, we can see some light.

Conclusions
As what we’ve seen in this section, coming up with a proof can sometimes involve a bit of ingenuity. But, sometimes, there is a “follow your nose” sort of approach that will allow you to devise a valid argument without necessarily displaying any great leaps of genius! [1]
Few bits of advice from J. Field in writing proof
- Before anything else, determine precisely what hypotheses you can use
- Jot down the definitions of anything in the statement of the theorem
- There are 26 letters at your disposal don’t be stingy with letters. The nastiest mistake you can make is to use the same variable for two different things
- Write a draft first. Write two drafts! Even if you can write beautiful, lucid prose on the first go round, it won’t fly when it comes to organizing a proof.
- The statements in a proof are supposed to be logical statements. That means they should be Boolean (either true or false)
- Don’t say “if” when you mean “since”. Really!
- Mark off the beginning and the end of your proofs as a hint to your readers. In our case, we wrote the word “Proof” to start off then end every proof with the abbreviation Q.E.D. (quod erat demonstrandum or “that which was to be demonstrated”)
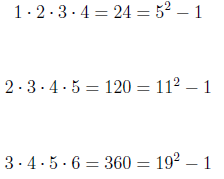


You got a 2.90% upvote from @minnowvotes courtesy of @sinbad989!
You got a 6.69% upvote from @nado.bot courtesy of @sinbad989!
Send at least 0.1 SBD to participate in bid and get upvote of 0%-100% with full voting power.
This post has received a 0.26 % upvote from @booster thanks to: @sinbad989.