A Gentle Introduction To Mathematics - Basic Notions of Set Theory
We're done with Chapter 2 of the book, GIAM. Today, we'll cover the notions of set theory. There was one profound statement from a teacher I had in college that I will never ever forget. In one of our class in algebra, he said that,
The mathematics foundation, all of the modern mathematics actually, is based on the concept of logic and set theory.
At that young age, I did not take him seriously. I don't understand what a set theory was at that time. But as I got involve in the mathematics of physics I started to get a glimpse of the power of that statement. This was strengthened when I started to take programming seriously.
When I encountered object-based programming, where everything about a problem is converted into an object, I started to appreciate the idea of "object" in a domain of knowledge. I realized then that every field of study in the world is about object and function. In physics, we have physical objects and dynamical rules. In mathematics, we have logic (functions) and set (objects). (a simple correspondence).
It was empowering to know that every knowledge in the world was reducible into its fundamental parts (objects and functions).
Disclaimer: this is a summary of section 4.1 from the book A Gentle Introduction to the Art of Mathematics: by Joe Fields, the content apart from rephrasing is identical, most of the equations are screenshots of the book and the same examples are treated.
Category Theory
In modern mathematics, there is an area called Category theory which studies the relationships between different areas of mathematics. The founders [1][2] of category theory noticed that essentially the same theorems and proofs can be found in many different mathematical fields – with only the names of the structures involved changed.
One can make what is known as a categorical argument in which one proves the desired result in the abstract, without reference to the details of any particular field. In this effect this allows one to prove many theorems at once- all you need to convert an abstract categorical proof into a concrete one relevant to a particular area is sort of key or lexicon to provide the correct names for things.
There are a good many mathematicians who deride category theory as “abstract nonsense”. But, as someone interested in developing a facility with proofs, you should be on the lookout for categorical correspondence. If you ever hear yourself utter something like “well, the proof of that goes just like the proof of the theorem” you are probably noticing a categorical correspondence.
Actually, the categorical theory doesn’t really save you that much effort. Then why are we mentioning category theory?
Because we are about to see our first example of a categorical correspondence. (Store the next sentence in your long-term memory)
Logic and Set theory are different aspects of the same thing.
The best description of a set is from Kurt Godel,
“A set is a Many that allows itself to be thought of as One.”
A more practical approach is to think of a set as the collection of things that make some open sentence true.
Logic and Sets
In logic, the atomic concepts were “true”, “false”, “sentence” and “statement”. In set theory, they are “set”, “element”, and “membership”. These concepts correspond to one another.
We can emphasize the connection between sets and open sentences in Logic by using a subscript notation. The set that corresponds to the open sentence P(x) will be denoted Sp, we call Sp the truth set of P(x).
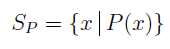
In logic we had “sentences” and “statements”, the latter were distinguished as having definite truth values. The corresponding thing in Set theory is that sets have the property that we can always tell whether a given object is or is not in them.
One can think of a set as being an unordered collection of things, thus the following sets are equal.
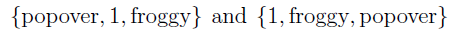
A set either contains or doesn’t contain a given element. It also doesn’t make sense to have an element in a set multiple times. By convention, if an element is listed more than once when a set is listed we ignore the repetitions. The following sets are really the same thing.
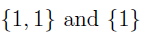
If the notion of a set containing multiple instances of its elements is needed there is a concept known as a multiset that is studied in Combinatorics.
In a multiset, each element is preceded by a so-called repetition number. For instances, consider the following questions: “How many ways can the letters of MISSISSIPPI be arranged?” Its equivalent multiset is expressed as,
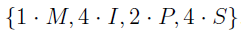
Sorted set
If a computer scientist were seeking a data structure to implement the notion of “set” he’d want a sorted list where repetitions of an entry were somehow disallowed. We’ve mentioned before that set is unordered, then why do we need it to be sorted then?
One reason is that we’d like to be able to tell whether two sets are the same or not. If the elements have been presorted it’s easier. Consider the following for instance,
| Unsorted Set | Presorted Set |
|---|---|
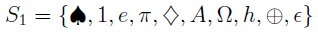 | 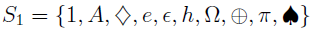 |
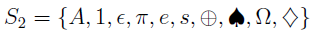 | 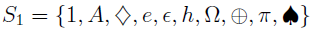 |
This business about ordered versus unordered comes up fairly often so it’s worth investing a few moments to figure out how it works.
One last interesting question: If you have a universal set of some fixed size, how many different sets are there? What’s the smallest possible size for a set? The standard answer is zero. A set with no elements is known as the empty set (note the definite article). A set of one element is known as a singleton set. An empty set is denoted by 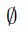 and there’s only one of it – irrespective of the universe we are working in.
and there’s only one of it – irrespective of the universe we are working in.
Power Set
Given a set of 3 elements,
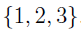
it is possible to construct a set, whose elements are all the possible sets in this universe. This set is known as the power set of the universal set. Indeed, we can construct the power set of any set A and we denote it with the symbol P(A), we have
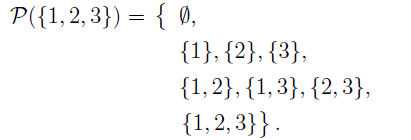


You got a 6.67% upvote from @luckyvotes courtesy of @sinbad989!
This post has received a 0.15 % upvote from @drotto thanks to: @sinbad989.
This post has received a 7.46 % upvote from @moneymatchgaming thanks to: @sinbad989. Upvote this Post to Support the MMG Community on Steemit! :)
You got a 7.29% upvote from @foxyd courtesy of @sinbad989!
Delegate Steem Power to this Bot and get 90% of the earnings. More Informations here.
For more information, click here!!!!
Send minimum 0.010 SBD|STEEM to bid for votes.
Do you know, you can also earn daily passive income simply by delegating your Steem Power to @minnowhelper by clicking following links: 10SP, 100SP, 500SP, 1000SP or Another amount