More scary notation

Previously, we tackled the basic objects of mathematics – the basic sets. The different types of numbers were discussed and introduced, and we had some exposure on translating mathematics lexicon into English translation. On the second post, we introduce the importance of definition and a very special set of numbers known as prime numbers.

In this post, we are going to delve into a more conceptual understanding of mathematics and discuss more scary notations.

Mathematical Theorem

Here is one important fact in mathematics: for every assertion, we have to prove that it is true for every or some element of some set. Consider the following assertion,

“Every number has an additive inverse.”

One should note that this statement depends on what is meant by a “number” and “additive inverse”.

The additive inverse of a is defined as the number b were a + b = 0; one way to say that is the additive inverse of a is the negative of a.

source

If we are talking about natural numbers the assertion is obviously false: 3 doesn’t have an additive inverse in natural numbers set. If we set the numbers to be integers (or any other sets that we’ve considered before excluding the natural numbers), the statement is, now, true.

Note that the sentence we had starts with “every”, it is an example of a universal quantifier. In other textbooks, it says “given any” or “for all”. The sentence we had holds true for everything within some universe.

It is probably clear that we are making assertions that a thing has an additive inverse, we are not discussing human beings, animals or a thing - we are talking about objects that add together: numbers of one sort or another. Now that we’re clear about the object of study we have, it is important to define explicitly what universe (universe of discourse) the objects we are discussing come from. Furthermore, we need to distinguish our assertations based on the span of its property.

Types of Quantification

1. Universally quantified: we assert that everything in the universe has some property
   Example: Pythagoras theorem

In any right triangle, the area of the square whose side is the hypotenuse (the side opposite to the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle). [1]

1. Existentially quantified: we assert that a few of the objects in our universe has some property

"For some airplane x there exists an airplane y such that x is faster than y"

In the previous posts, we discuss a few lexicons: such that, an element of, not equal to, a set of, is equal. Today, we add another translation lexicon to our mathematics glossary: an upside-down A which translate as “for all” for universal quantification and backward E, which translates to “there is” or “there exists” for existential quantification.

Now, let’s try to capture the meaning of the assertion which we started with:

“Every number has an additive inverse.”

This can be written in mathematical notation as:

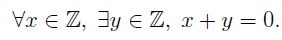
the English translation of this lexicon is

Let's have some simple exercise to solidify your understanding.

Which type of quantification do the following statements have?

1. Every metallic element is a solid at room temperature.
2. Everybody has some friend that think they know everything about some sport
3. There’s someone for everyone.
4. Some days it’s just not worth getting out of bed.
5. Every man loves a woman

References:

1. https://en.wikipedia.org/wiki/Quantifier_(logic)
2. A Gentle Introduction to the Art of Mathematics by Joe Field
3. https://link.springer.com/chapter/10.1007/978-94-017-2817-1_11

---

Thank you for reading ...