The paradoxical cake of Cantor
Hi Steemians, today another story about two of my greatest loves cake and math!
.jpg)
Mister Cantor is the proud owner of the infinity patisserie which is located in the center of the city Mathematica. It is popular for its Koch flake cookies, Menger sponge cake and Feigen-baumkuchen. On Wednesdays, the patisserie chef Cantor produces a most delicious one meter long strawberry cake. From the top it looks something like this

Observe that Cantor placed small notes to indicate the edges of the cake. 0 is the left edge and 1 is the right edge. So a position on the cake, which is referred to as a cake-position, can take any value between 0 and 1. The cake is described by its edges. So we will denote the whole cake as an interval: [0,1]. The customer can decide how much of the cake he/she wants and Cantor will cut it accordingly.
The first customer
This Wednesday Cantor's first customer is a tall gentleman. "I would like to buy 0.8 meter of your strawberry cake. But the side of the cake is always a bit dry. Would it be possible to get a 0.8 meter middle part?"
"Yes, the customer is king after all!" Cantor replies. So Cantor cuts the cake, puts the cake in a nice box, which then goes into a nice big bag which results in one overjoyed customer. After the customer has left Cantor places two additional small notes to indicate the edges of the resulting two cakes:

A piece of cake is described by the location of its edges. So we denote a cake piece in interval notation. The cake intervals which are left are then described by [0,0.1] and [0.9,1]. So in total Cantor has sold 0.8m. In cake-position notation this corresponds to all the cake-positions for which the first decimal after the dot is a 2,3,4,5,6,7,8.
More enter
Shorly after, a married couple enters. "We would like to buy two pieces of 0.08 meter. But could we have the middle part?" the wife asks.
"Yes, of course!" Cantor replies. He cuts the four pieces, packages everything and two satisfied customer leave his patisserie. Cantor then places notes to indicate all the edges:

So the cake intervals which are left are [0,0.01], [0.09,0.1], [0.9,0.91] and [0.99,1]. In total Cantor has sold 0.8 + 2 x 0.08=0.96m. In cake-positions this corresponds to all cake-position for which the first or second decimal after the dot is a 2,3,4,5,6,7,8.
Now a family of four enters. "Could we get four pieces of 0.008 meter of the middle parts?"" the husband asks.
"Yes, no problem!" Cantor replies. He cuts four pieces, packages them and a happy family of four leaves his shop. Unfortunately, the pieces became too small to write clear notes. But the cake now looks like this:

So the eight pieces which are left are given by the intervals [0,0.001], [0.009,0.01], [0.09,0.091], [0.0999,0.1], [0.9, 0.901 ], [0.909 ,0.91], [0.99,0.991 ] and [0.999 , 1]. In total Cantor has sold 0.8 + 2 x 0.08+4 x 0.008=0.992m. In cake-positions this corresponds to all cake-position for which the first, second or third decimal after the dot is a 2,3,4,5,6,7,8.
Next 8 customers enter who each want a 0.0008 piece. And yes, they only want the middle parts. In total Cantor has sold 0.8 + 2 x 0.08+4 x 0.008+8 x 0.0008=0.9984m. In terms of cake-position he has sold the cake-positions for which the first, second, third or fourth decimal after the dot is a 2,3,4,5,6,7,8.
Next 16 customers enter who each want a 0.0008 piece. And again, only the middle parts of what is left. Then 32 come in who only want a 0.00008 piece of the left middle part pieces. This continues the whole day. In the city of Mathematica the day takes an infinitely long time. At the end of this day Cantor calculates how much cake he has sold:
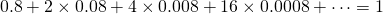
He concludes that he has sold the whole cake (see the technical appendix for the proof)! In terms of cake-positions he has sold the cake-positions for which any number after the dot is a 2,3,4,5,6,7,8.
Left-overs?
When Cantor looks over to the cake he can see that there is still some left. "Well I did never cut the cake's edges. So probably what is left are the cake edges." he mumbles to himself. Cantor realizes that all cake edges have the property that they can be written as a whole number times 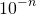 for some whole number n. For example, 0.999 is a cake edge and it can be written as
for some whole number n. For example, 0.999 is a cake edge and it can be written as 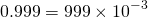 . But this also means that the cake position 1/11=0.090909090... is not a cake edge since it cannot be written as a whole number times
. But this also means that the cake position 1/11=0.090909090... is not a cake edge since it cannot be written as a whole number times 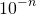 . But Cantor has sold the cake-positions for which any number after the dot is a 2,3,4,5,6,7,8. The number 1/11=0.090909090... has no 2,3,4,5,6,7,8 appearing in it. Since it cannot be a cake edge it is still inside the cake! He exclaims:
. But Cantor has sold the cake-positions for which any number after the dot is a 2,3,4,5,6,7,8. The number 1/11=0.090909090... has no 2,3,4,5,6,7,8 appearing in it. Since it cannot be a cake edge it is still inside the cake! He exclaims:
" I am left with a paradoxical dessert!"
.jpg)
Photo by Laika AC
Conclusion/Reflection
Let us call the cake obtained after cutting away infinitely many pieces the Cantor cake. I derived the paradoxical property that altough the cake was originally 1 meter, when cutting away pieces with a total length of 1 meter to get the Cantor cake you end up with something that is more than just points.
What is the intuition behind this?
Before we can answer this you first need to realize that after having removed infinitely many pieces you do not end up with a collection of intervals. To see this observe that 0 must be an edge of the Cantor cake well what is the smallest edge greater than 0? You might say 0.0001 is a small edge point, but it is not the smallest since 0.00001 is also a edge point. Is this the smallest? No, since 0.000001 is smaller and again this is not the smallest. So you cannot think about the Cantor cake as something which is equal to a collection of intervals. Informally, you can describe it as follows
altough the Cantor cake is constructed by removing cake-intervals it is not equal to a collection of intervals. Thus, it transcends the natural intuition that we have for intervals.
When dealing with the Cantor cake you cannot rely on your intuition anymore since it is not in the realm of ordinary logic. And that is why you need the power of mathematics to lead you the way.
Further reading/sources
The mathematical object that this cake corresponds to is called the Cantor set. It has many more counter intuitive properties. Conventially, the Cantor set is explained in base three (counting when you have three fingers) but I did it in base ten since it does not require any knowledge about number bases. However, the theory for the base three Cantor set is identical to the base ten Cantor set since there is way to transform one into the other. If you want to find a more formal approach to Cantor sets you can have a look at the wiki-page over here. You can also checkout this book Understanding Analysis by Stephen Abbott (Springer, 2002).
The top photo is by Hedwig Storch
The figures where made using inkscape and all the equations were written using quicklatex. They are both free to use!
Technical appendix
The sum can be written as
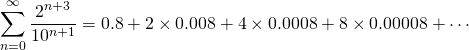
as is made clear by the right hand side. This is a geometric sequence which is equal to one. For the wiki click here
Thank you!
Thanks for being so kind to read my post. You are awesome! Please follow me if you enjoyed it. If you have any questions just post them below and I will answer them. Or if you might have a nice topic you want me to cover also let me know below. :o)

This is a test comment, notify @kryzsec on discord if there are any errors please.
Being A SteemStem Member
I love the way this article begins with baking jokes about Koch, Menger, and Feigen fractals. And I am avid to understand more about Cantor's work, which I think you know well enough to teach me.
Yet my understanding hangs up on a single phrase that you use a couple of times. The phrase is "consists out of" (something — in this case, intervals).
At one point you say, "… you do not end up with something that consists out of intervals." At another point you say, "although the Cantor cake is constructed by removing cake-intervals it does not consist out of intervals."
I confess I am baffled by this phrase. "Out of" can mean so many different things, and some of its meanings are opposites. When you build "out of" bricks, it means bricks were plentiful, but when you run "out of" bricks, it means bricks were lacking. And I have never before encountered the word "consists" preceding "out of."
Does "consists out of" mean the same thing as "consists of"? Or does it mean the opposite? Please forgive my failure to take your meaning. Thanks in advance for explaining!
Thanks for the support and the reply. Yes you are right it is not very clear. Sometimes I directly translate Dutch expressions to English. In this case it becomes very unclear.
So mathematically, when I am talking about "consists out of intervals" or "consists of intervals" I mean that you can write it as the union of intervals.
Thanks for mentioning it. I will adjust the post in bit.
Now I get it. Thank you!
This is similar to the concept behind Zeno's paradox, right?
Nice question. They are a bit related. Zeno's paradox is connected to the mathematical definition of limits. In addition, if you understand limits Zeno's paradox is not really a paradox. In this case, the problem is still related in a sense to limits, however, understanding limits in the sense of Zeno's paradox is not sufficient to understand what is going on here.
I find this in particular really interesting. I had never thought about it like that! I'll try to dig a little into Cantor's work for better understanding since right now this is a little above me.
Great post!
Thanks as always for your support.
So it even gets crazier because in a sense there are the same amount of distinct points in a Cantor set as there are on the real line. (Or more formally, the cardinality of the Cantor set and the real line is the same)
I don't think I need to explain that I like your articles anymore, I think this is evident by now. Question: So if a day takes an infinite amount of time, and he only makes that cake on Wednesdays, is there any other day of the week in that world? Because supertasks can't apply here, if a day was as long as he needed to sell all the cake, and he would need half the time to sell the next interval of cakes than the previous one, there would be an end to the day. But since you've defined the day to have an infinite amount of time, there can't be another weekday.
Am I reading too much into the plotholes of an article on fractals?
But I never tire of hearing it :P
Haha nice one. Yes, you are right, an infinitely long day does not have an end. I used it as a story-telling tool as opposed to being mathematically or physically correct. :o)
OMG! Whatta delicious way to present Math!
Waoo great post i enjoin the reading ..thanks for your post
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by MathOwl from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Nice article. :)
Thanks :D
Interesting topic once again @mathowl! The notion of flake cookies and cakes made me read all the way down the bottom though my nose bled for a while :D
Good to see another weird thing from math that you've mentioned can be likened to a line. Its nice chef Cantor had some cake left for dessert paradoxical it may seem.