The mathematics behind medieval battles
Hi Steemians! Today I will treat a simple mathematical model for medieval battles. This post is mostly written as a story. So I think it is easy to read. Technicalities have been put in a separate section at the end. :0)

The mission
Suppose you are an army general in medieval times. An evil Baron has assasinated the King's youngest son. So the King has sent you to invade the Baron's lands to slaugther him and his men. You have a total of 2000 infantry soldiers under your command. Your whole army is armed with spears.
Scouting
The day before the invasion you have sent scouts to your enemy to see how large their army is. When the scouts come back they have good and bad news. The bad news is that the Baron received reinforcements and now has 3000 infantry ready. Furthermore, these soldiers are armed with spears and all seem equally well-trained as yours. The good news is that the Baron's army is divided over three different locations. They hand you a map:
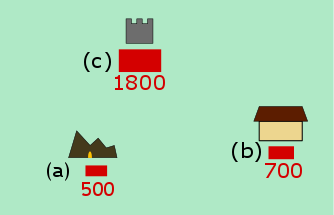
500 men are stationed at the Baron X's gold mines, location (a), 700 men are protecting the Baron's graneries, location (b), and another 1800 men are located at the Baron's palace, location (c). They also mention that these three locations are quite a long distance away from each other. So the Baron does not have enough time to send reinforcement when one location is attacked. The scouts also drew you a nice overview of the situation:
Strategic idea
So what are your strategic options? It makes sense to not split your forces but keep them all together. Which location should you attack first (a),(b),(c)? And where to attack next? Does it even matter? To answer these questions you need information about how many causualties are suffered during each battle. These answers will be given by a modelling the battle process.
Lanchester battle model
Fortunately, Archmaester Lanchester has offered his services to help you with the mathematical model. The Archmaester takes out his quill and a big piece of paper and says "Let us first begin with assumptions".

Source
"I will assume that since spears are long weapons. That soldiers on both sides are in striking distance of the enemy"
"My recent documentation shows that one of our soldiers kills on average 1/10 enemy soldier per minute. We will assume that is also the case for the Baron's soldiers "
"And now for some notation. Let t denote time per minutes with t=0 corresponding to the start of the battle. Denote by A(t) your army size at time t and by B(t) the Baron's army size at time t. Consequently, A(0) your armies' starting size and B(0) equals the Baron's army starting size."
"So we observe: our casualties per min at time t is B(t)/10, similary, the casualties per min at time t for the Baron is A(t)/10.
Archmaester Lanchester then starts writing down symbols you have never seen before (If you are interested in what he writes down check the technical appendix below). After a few minutes he arrives at the following two formulas:
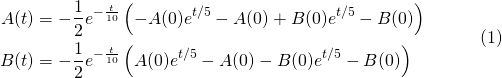
"The battle is won at a time t=T when the Baron's soldiers are reduced to zero, B(T)=0, and the battle is lost at a time t=T when your soldiers are reduced to zero, A(T)=0. Armed with these formulas you can predict everything "
Results
Recall that 500 (a) 700 (b) 1800 (c). Then using Equation (1) you can write down all the possible battle scenarios and see if you will win and compute how many soldiers will survive:
(a)->(b)->(c) : 141 soldiers survive
(a)->(c)->(b) : 141 soldiers survive
(b)->(a)->(c) : 141 soldiers survive
(b)->(c)->(a) : 141 soldiers survive
(c)->(a)->(b) : 141 soldiers survive
(c)->(b)->(a) : 141 soldiers survive
You make the observation that it is does not matter (the reason for this is given in the Technical Appendix)! You always win! So finally you can rest assured that you will defeat the Baron!

God Speed - Edmund Leighton
Conclusion/Reflection
In the current setting we computed that independent of where we attack we will always defeat the Baron with the same amount of casualties. Now suppose that the Baron would have rearranged his soldiers in the following way: 300 (a) 800 (b) 1900 (c). Using the formulas in (1) you will see that it is not possible to defeat the Baron in any scenario. Concluding:
The distribution of the Baron's soldiers over the three locations determines if you can defeat him or not
Of course it should be noted that this is a highly simplified model. Battle formation, moral etc. are not included in this model. In addition, we expect that the casualties taken is a discrete process. However, in this model it is continuous since the Equations (1) can be evaluated for any t.
Sources and Further reading
Source top photo - Battle of Grunwald by Jan Matjeko
The model treated in this post is the most simple version of the Lanchester model. For the wiki click here. I gave my own spin on explaining it.
This model is connected to predator-prey models. More specifically, it is connected to Lotka-Volterra, see this wiki.
Equations written using Quicklatex it is free to use!
Second figure made using Inkscape
Technical appendix (for those who completed a calculus course)
The equations resulting from Archmaester Lanchester's modelling assumptions give a linear ODE:
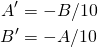
Since it is a linear ODE it is easy to compute solution vectors and the flow.
Recall that in the result section we obtained the same results for any battle scenario. By using the equations in (1) you can prove that independently of the distribution of the Baron's soldiers the final result is fixed. In a mathematical setting we say that the underlying operators commute.
Thank you!
Thanks for being so kind to read my post. You are awesome! Please follow me if you enjoyed it. If you have any questions just post them below and I will answer them. Or if you might have a nice topic you want me to cover also let me know below. :o)

Being A SteemStem Member
The interesting thing about the model is that it seems to work better for armies where numerical superiority is key to winning as the objective is to reduce enemy army to 0, however medieval armies would require a much more complex model, not least because of equipment, movement speed and morale, but the disadvantage of commanding a massive army. Your cover photo for instance, the impressive battle of Grunwald was won due to tactical manoeuvrers and not numbers: though the winning side was numerically superior it was the speed of the initial light cavalry attack, the retreat and then coordination of wing movements that clinched the victory. Good examples of numbers not being of much use when countered with discipline and formation are Cannae and Vienna. Still, I'm no expert but this seems to be a better model to predict modern infantry facing off, great work though!
Yeah I totally agree that this is a highly simplified model which does not take into account crucial aspects of medieval warfare. But it is possible to extend this model. More specifically, it is not too difficult to set up equations per unit-type so that you can determine a possible outcome when two types of units meet in combat for a given time interval.
Very well done as always. I remember having seen a video (most likely by numberphile, anyone who subscribed to your blog should check them out) related to this wherein they calculated wether splitting up your troops and attacking an army in waves makes sense or not. If I find it I'll post it here as well, it's quite an interesting calculation as well.
Please do. I am curious if they used a different model and got a different result :0)
I am very sorry but I can't for the life of me find the video. I can't remember what the name was and/or what channel I saw it on. I'll keep it in mind if it should ever come up again in my recommended videos and I'll immediately contact you.
okok thanks
Wow, I never thought mathematics can be used this way. Interesting application! Tides of battles would have been turned if they used these concepts long ago.
For modern applications I think this can be used in AI battle simulations for games. Thanks for the interesting good read!
The Lanchester model is a very simple model. I think that computer games like the total wars series give a way more accurate representation of ancient warfare since they model everything discretely.
However, it is possible to extend this model to take into account more advanced battle concepts like moral, flanking, etc.
Must be interesting to see how moral and flanking will transform the battle equation's results. Its really nice that you bring such nose-bleeding concepts into laymen's terms with your stories, please continue to do so. Hoping to read more good readings from you.
(P.S.: Would be great to hear an equation-driven story about how scientists can help farmers predict which crop will yield the best profit or which crop is the best to plant for a specific month or day) TIA! :P
I think I will write a weekly story-math post and a weekly abstract-math post.
PS Nice idea. However, the problem with crop-growth/harvest equations that they are not really derived in a natural way. I think they essentially are derived experimentally. So the equations don't arise as natural as in this post.
I see, thanks for your input. I also think there are a lot of factors to consider for that, you might end up writing a novel.
I'm looking forward for your upcoming story-math posts (and try to dabble with the abstract ones too :D)
WHAT DID I JUST READ????? OH WOW, I may not be a math major, but you just turn history into a mathematical strategic analysis! applause because such skill is not my forte, your post amazes ppl. I wonder if all maths person see things mathmatically
Great that you enjoyed it. Well I think mathematicians are humans. However, they have the magical ability to pull the real word in to the world of abstraction.
It was a pleasure to read your article. I am surprised so many people enjoyed it. When I post about science I get little to no engagement. Perhaps I need to follow your followers more :D
I am also surprised so many people enjoyed.
Well from today onwards you have a new follower ;)
Thanks! I will also try to post in #science more times than not.
Apply ODE in real life, wow. As an Engineer student, we use ODE mainly for calculation, never thought of something this cool. *Ehem war
You better not use it to model the battle success of your engineered killer robots ;)
ODEs can be applied to predator-prey wildlife scenarios and mathematical biology. A natural extension of ODEs is Partial Differential Equations (PDEs) where the focus is on partial derivatives. PDEs are used by (applied) mathematicians and engineers.
Great job on introducing Math concepts, @mathowl! This is a great read. I was able to follow up until the calculus formula 😂
Continue posting about math topics with a twist. Cheers
Thanks for the support :)
wow I found a new teacher!
@masterwu has stuff which is more related to a math curriculum. Check him out if you haven't already. My stuff is more recreational :o)
Fascinating! I never would have thought a version of the "Predator-Prey" would have been applied in such away. Well done.
Thanks. Also nice work on the cup of hot chocolate problem.