Pushouts on Graphs

A "graph grammar" is a set of rules that rewrite graphs, just as a context-free grammar or context-sensitive grammar rewrites strings of symbols.

The algebraic framework for understanding graph grammars is Double pushout (DPO) graph rewriting, but that article is nearly completely uninformative. The longer explanation at https://en.wikipedia.org/wiki/Graph_rewriting#Algebraic_approach is complete word salad as far as I can tell. It boggles me that somebody tried to explain a category-theory concept without making a diagram.

So I think I can do better, and I'm reading this technical report which builds this construction up with every detail covered:

• Alfio Martini, Graph Grammars -- An Introduction to the Double-Pushout Approach, Report 6, Fachbereich 13, TU-Berlin - Informatik (1996).

I'll try to be a little more user-friendly by not including any proofs. :)

Pushouts

Let's start with some preliminaries, looking at single pushouts and what they mean in the context of graphs or labelled graphs.

A "pushout" is a category-theory construction. The input is two functions ("morphisms") with the same domain ("object"). The output is a special object P (for pushout) and two functions entering it.

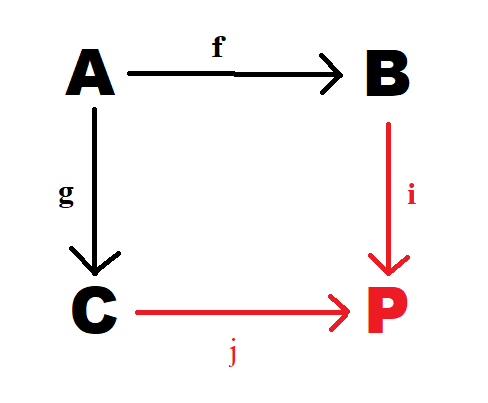
Black = input functions f (which goes from A to B) and g (which goes from A to C)

Red = output object P, and functions i and j.

We can say: P is the pushout of f and g, just like in other contexts we might say R^2 is the product of R and R.

This is a commutative diagram, which means that the two paths between A and P are equal, that is, i(f(x)) = j(g(x)), or i ○ f = j ○ g.

What makes P special is its relationship with other objects that might satisfy the commutative diagram. It's sort of the "smallest" object that does so. For any other object Q (with its own pair of functions that work with f and g), there a unique function, labelled '!', that makes the diagram commute:

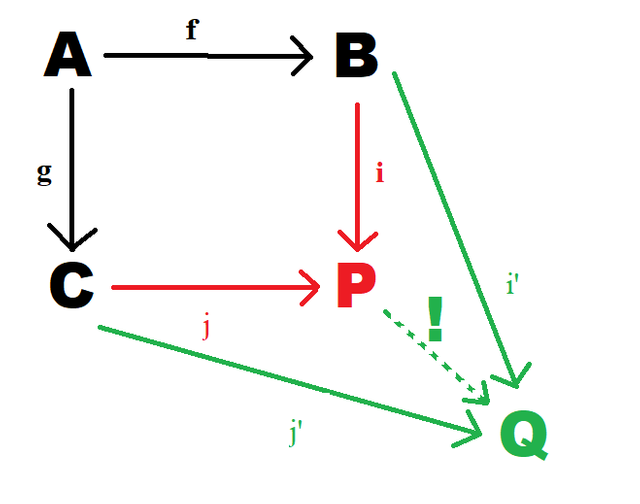
We can think of Q as a candidate for P's job. P comes out ahead by showing that there's only one way to get from P to Q that is compatible with the rest of the functions. If P beats Q and Q beats P then they must be isomorphic.

Example: Sets

All the examples in Wikipedia on this topic are nearly incomprehensible, too.

Let's start with ordinary sets. P can be made from the "disjoint union" of B and C. A disjoint union means the result remembers whether an element came from B or from C; you can think of this as labeling or coloring the elements of B and C. In fact, if you left off f and g you'd get a different category-theory construction called the coproduct.

The effect of f and g, though, is that P considers elements of B or C that originally "came from" A to be the same element.

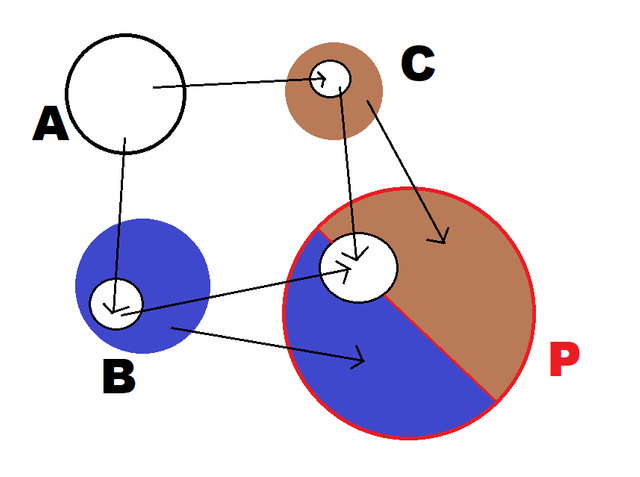
Suppose x is an element of the set A. Then f(x) is an element of B and g(x) is an element of C. So there's an image of A inside both B and C, represented by the white circles above.

In the pushout P, those two images get smashed back together. Remember, i(f(x)) = j(g(x)) from the commutative diagram. All the other elements of B or C (if there are any) stay separate, the brown and blue portions of the diagram.

Let's make it even more concrete. Let's say

A = { 1, 2, 3 }
B = { red, green, blue }
C = { Steem, Bitcoin, Ethereum }

f(1) = red
f(2) = red
f(3) = blue

g(1) = Steem
g(2) = Ethereum
g(3) = Bitcoin

Then what is P and what are the functions i and j?

Well, we need i(f(1)) = i(red) and j(g(1)) = j(Steem) to be equal when they get brought into P by the functions i and j. Similarly, i(red) = j(Ethereum) (starting with 2) and i(blue) = j(Bitcoin) (starting with 3.)

P = { red, green, blue }

i(red) = red
i(green) = green
i(blue) = blue

j(Steem) = red
j(Ethereum) = red
j(Bitcoin) = blue

We could have used different labels for P if we wanted to. We can also see that if we try replacing P with a larger set Q like { red, green, blue, yellow } then the conditions force us to map P-red to Q-red, P-green to Q-green, and P-blue to Q-blue; there's no way to map something to yellow and still have the functions be consistent (i.e., for the diagram to commute.) So we can only map from P to Q in one way (and that way works.) But the reverse direction is not the same; we could map Q-yellow to anything at all and it would be consistent. So P->Q is unique, but Q->P is not, so P wins.

Morphism on Graphs

First, what is a morphism on a graph?

A graph morphism (a function that preserves the graph structure) comes in two parts: a function from vertices to vertices, and a function from edges to edges. These need to be consistent so that if the morphism maps vertex X to vertex Y, then the edges starting at X should all be mapped to edges starting at Y. We can show that as a commutative diagram, too:

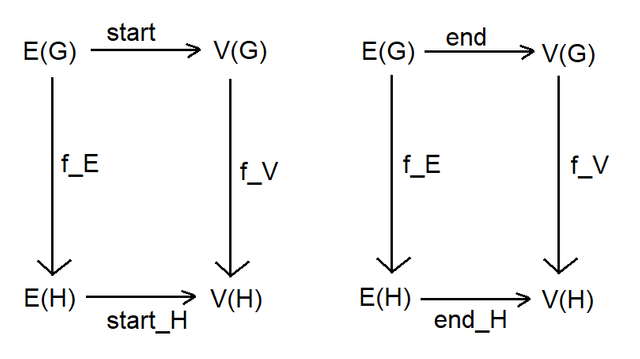
E(G) = edges of graph G, V(G) = vertices of graph G

The "start" function specifies out the start vertex given an edge, and the "end" function specifies the end vertex for an edge. (We can think of these as "attributes" of the edge, or as functions on the domain of edges; the two are mathematically equivalent.)

The graph morphism "f" is from G to H. Its action on edges is labeled "f_E" and its action on vertices is labelled "f_V"

To be really concrete, here's a picture of a graph morphism. Note that it's not a function on graphs, plural, it's a function on one specific graph! It doesn't take a graph as an argument, it operates on the nodes and vertices of the graph that is the moprhism's domain.

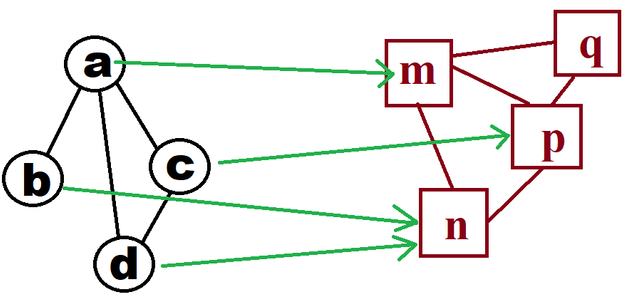
The morphism takes a->m, b->n, c->p, d->n. So it must take edges (a,b) to (m,n), (a,d) -> (m,n), (a,c) -> (m,p), and (c,d) -> (n,p).

Pushouts on Graphs

Now, finally, what does it mean to take two graph morphisms (f from A to B, and g from A to C) and construct their pushout?

We can think of each part of the graph morphism individually. Looking at just the vertexes, the pushout has to act like it does on sets. The vertices that are the image of A in B and C have to come back together to be the same vertices in P:

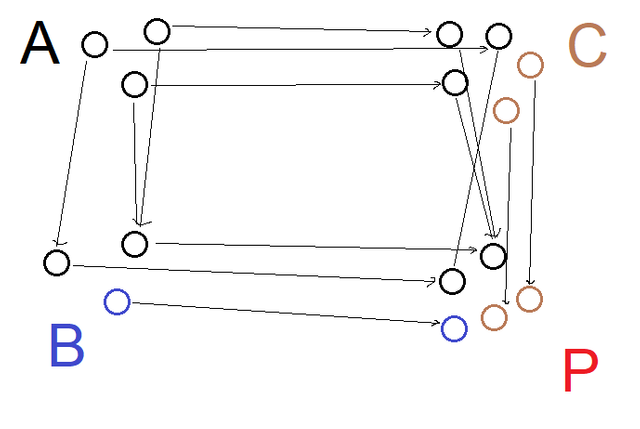
If our graphs had no edges, this is all the work we'd have to do! If A,B, and C have edges, then f or g might either collapse two edges into one (including possibly a self-loop, which seems to be allowed in this context) or map vertices that weren't connected into ones that are. The maps i and j have to preserve these properties, but fortunately they mainly just fall out from the decisions we made on individual vertexes.

For example, suppose A has no edges, B adds one edge to a blue node, and C has lots of extra edges. Then the pushout needs to have all the edges from B, and all the edges from C. But because A->B mapped 1and 2 to the same node, that has to carry through to P as well, so the edge between 1 and 2 in C gets squeezed into a self-loop in P.

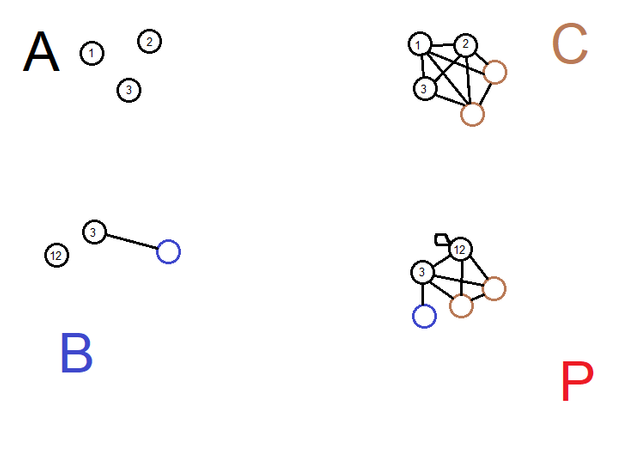
How do we know that this is the pushout? Suppose our "candidate" Q had an extra edge that P does not; then we could still create a morphism from P to Q, but not the reverse. On the other hand, if Q collapses extra nodes and edges together, then we can create a morphism from P to Q in exactly one way (collapsing the vertices that Q collapses) but from Q to P in more than one way (the collapsed vertex could be mapped to either one of the vertices that it came from.) If Q is missing an edge altogether, then we can't make its diagram with f and g commute.

Application to Graph Rewriting

We can treat the graph morphism A->B as a "rule" for changing A, and the morphism A->C as "the location of A in the graph C. Then the pushout P looks like "apply the change between A and B, to the graph C".

For example, here the difference between A and B is the addition of a blue edge. The morphism B->P has to put that edge somewhere. The morphism A->C "identifies" nodes in C that correspond to the pattern of A: three vertices, two of them connected. The pushout's universal property ensures that the vertices which were "changed" by B and "identified" in C map to the same vertices in P.

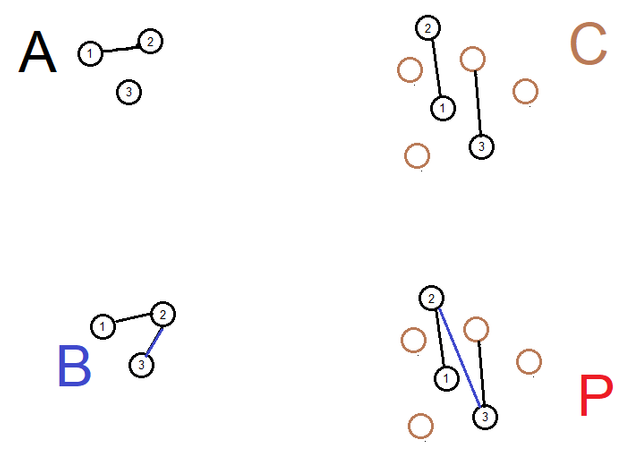
Of course, the diagram is symmetric so we can read it in reverse order! In this case, we can equally well interpret C as the rule which is "add an edge and a bunch of unconnected brown nodes", which gets applied to the graph B, whose blue edge which is not part of the pattern gets preserved. But this is because both morphisms are injective (1-to-1) in this example. For general use, we require that only one of the morphisms be injective: the one that identifies where the pattern resides in the target graph we are going to modify.

Conclusion

The pushout is certainly not a well-known structure. But we can see that it encapsulates what we want from a graph rewriting rule: "make all the same changes, but don't leave out anything or add anything extra." This sort of universal property occurs over and over again in category theory, and many types of categories are defined by what sort of constructions are available. In the category of Graphs (and Labelled Graphs, which I didn't get into) the pullback is always present; adhesive categories are a generalization that has this property.

The limitation of a single pushout is that we can't delete a node or edge; we can only merge it with some other node. Double pushouts are supposed to fix this, but I have more reading to do before I can draw a diagram for how that works.

Further reading on category theory

Part 2 is now available: "Double Pushouts on Graphs".

• Universal Property -- Wikipedia: the class of constructions to which pushouts belong
• Saunders Mac Lane, Garrett Birkhoff. "Algebra", American Mathematical Society, 1999. A textbook on algebra which uses category theory and universal constructions throughout, augmenting the more conventional axiomatic approach. (I have the 1968 edition, I believe?) Aimed at undergraduates, so more accessible than some.
• William Lawvere, Stephen Schanuel. "Conceptual Mathematics: A First Introduction to Categories", Cambridge University Press, 2009. Also a very accessible introduction, lots of simple examples.