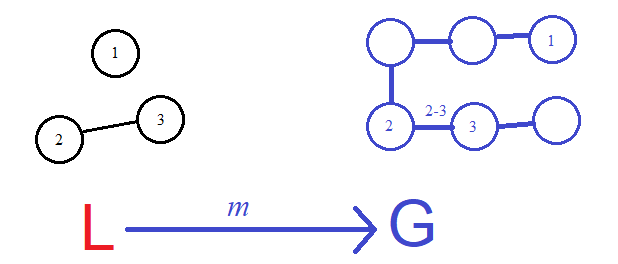Double Pushouts on Graphs

In the previous article I introduced graph grammars and their representation as a "pushout", in category-theory terms.

Graph grammars which only add or merge vertices and edges can be represented as a single pushout. But when we want a rule which deletes vertices or edges, we need to switch to a "double pushout". As my godson would say, "what does that even mean?"

As before, I am heavily reliant upon

• Alfio Martini, Graph Grammars -- An Introduction to the Double-Pushout Approach, Report 6, Fachbereich 13, TU-Berlin - Informatik (1996).

though the illustrations and examples are my own.

Double Pushout Commutative Diagram

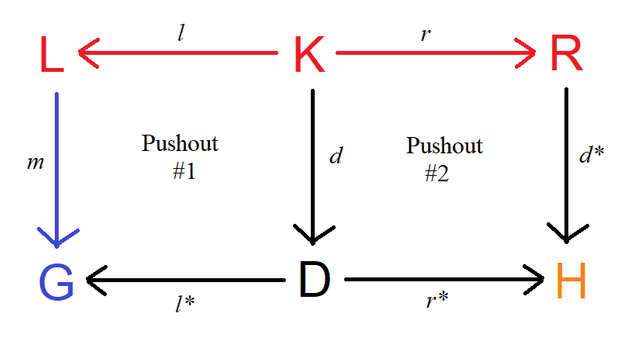
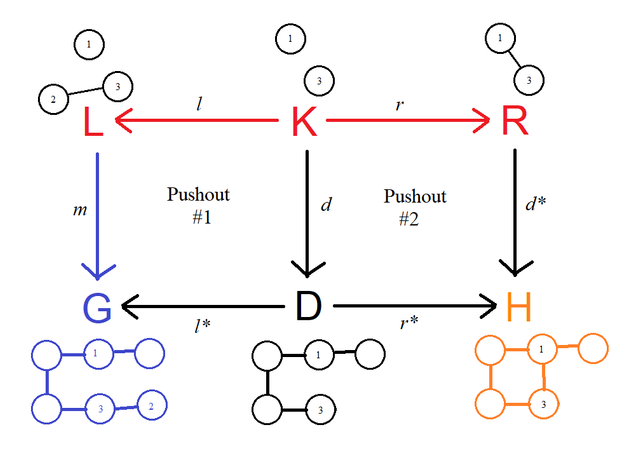
Punchline first. Here's where we are going to end up, as a commutative diagram.

The red components are the "rule". We want to transform a pattern that's represented by the graph L into the resulting graph R.

The indigo (blue) components are the "input" or "match". The graph G is our input to the rewrite rule, and we find an example of the pattern L in it via the graph morphism m.

The orange components are the "output" or "derived graph." Applying the rule to G results in the graph H.

D is an intermediate computation step.

The diagram has two pushouts connected by g. G (our input!) is the pushout of l:K->L and g:K->G. The output H is the pushout of r:K->R and g:K->G.

Let's go through these pieces one by one and build up an example.

Breaking the rule apart

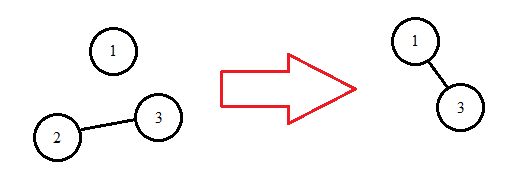
Here's a graph rewrite rule that takes three vertices: 1, 2, and 3. There must be an edge between 2 and 3 (other edges may exist but are not specified). The rewrite is to delete 2, and the edge 2-3, but add an edge 1-3.

This doesn't work as a graph morphism; it is only a partial function. 1 on the left maps to 1 on the right, 3 on the left maps to 3 on the right, but vertex 2 and the 2-3 edge don't map to anything at all.

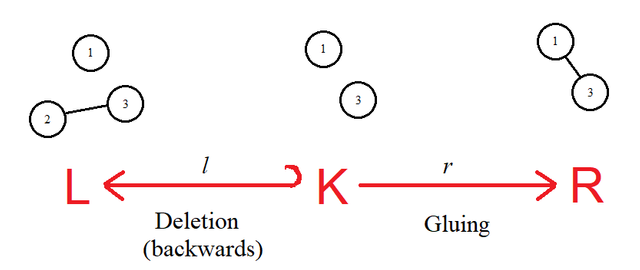
In order to express this relationship in terms of graph morphisms (complete functions) we break the deletion and the "gluing" into two separate steps.

The morphism l maps from the undeleted elements in the graph K back to the original pattern L we wanted to match. The morphism rmaps from the undeleted elements to the transformed graph R we want to make by merging or adding new elements. Both these morphisms are complete functions; the only restriction is that we want l to be an injective function; category theorists sometimes draw this with an arrow that has a hook on the end like shown here.

If we don't have any deletions, then L=K and the morphism l is just the identity morphism on L.

This construction in category theory is called a span.

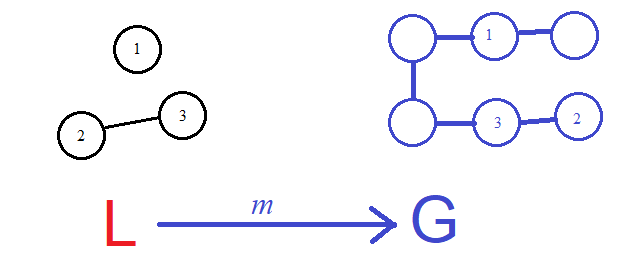
Finding a match

Here's a "match" that finds the pattern graph L inside the source graph G. This looks just like what we were doing before with single pushouts.

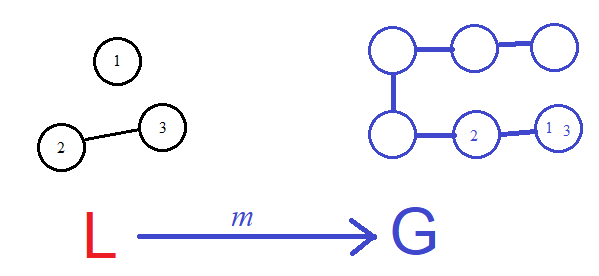
However, not all matches "work" correctly. Suppose instead we tried to do this:

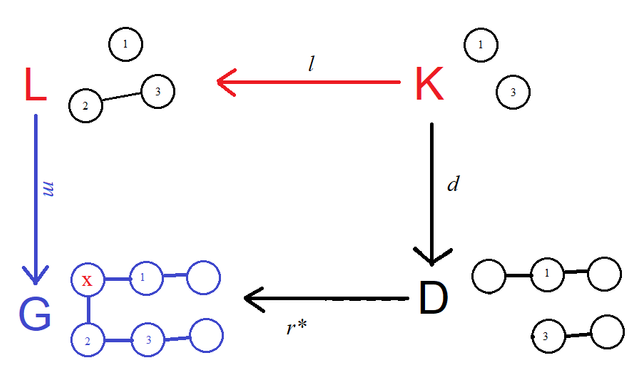
when we delete 2 (and the edge 2-3), what happens to 2's other edge? Just leaving it dangling is unacceptable; on the other hand, if the rule wanted that edge deleted, it probably should have told us so explicitly. (In Martini's article this match violates the "dangling condition", which he defines precisely in terms of the mapping between K and L.)

The match doesn't have to be injective; something like this is fine:

but if we tried to map 1 and 2 in K to the same vertex we'd run into another semantic problem: we're supposed to be deleting 2, so where will our new edge go? Martini's terminology is that the match should satisfy the "indentification condition" and avoid "identifying" two vertices or edges to the same element of G if one of them is going to be deleted.

The good news is that in the next step those conditions automatically fall out of constructing a pushout! (Sometimes category theory really does pay off; we can change a lot of goop about conditions have to hold into a universal construction which may not be simple to understand but is at least defined in a straightforward, consistent fashion.)

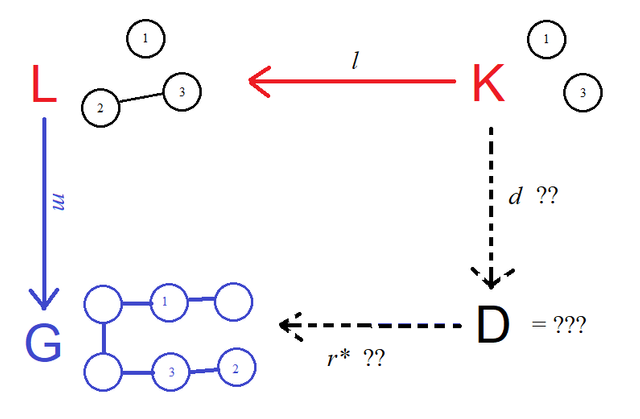
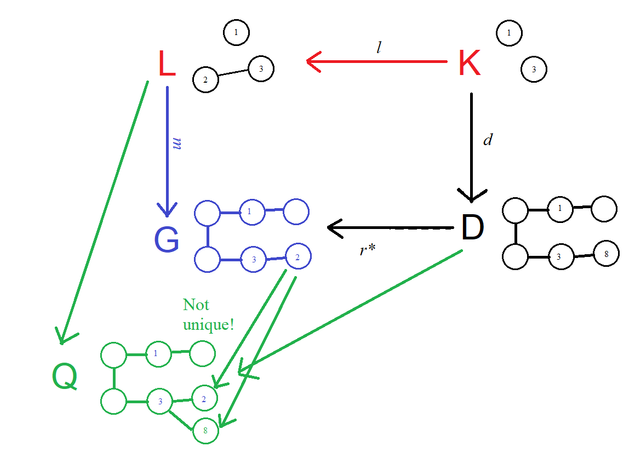
Deleting elements from G with a pushout

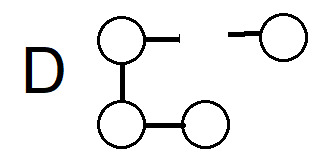
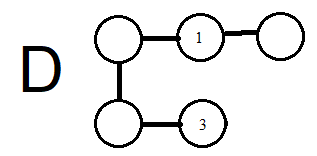
The "intermediate" graph D is a version of G with all of the elements deleted, that the rule specifies to delete.

But, to make it we're running the pushout construction partially in reverse. Instead of being given l : K -> L and d : K -> D and constructing G, we're given l : K -> G and m : L -> G and being asked to find D and d such that the resulting square is a pushout. This can be referred to as finding a "pushout complement".

Fortunately, this can be done in a straightforward way. Informally, we want D to be "G, but with the deletions." We know that if G is a pushout, then the nodes are a disjoint union of nodes from L and from D. So if there are nodes and edges that appear in G but not in L, then they had better be coming from D.

In the other direction, nodes 1 and 3 in graph K have to show up in D somewhere. The commutativity of the pushout says that the 1 we get from the left-hand path though L and the 1 we get from going through Dhave to end up in the same place, and the same with 3. The only way to make that work conveniently fills in our missing vertex:

Now we can verify that G is in fact the pushout, as desired. But is the only way that it works? What if we added another vertex into D as well? That creates a commutative diagram, but G no longer has the universal property that defines a pushout. For example, graph Q make the diagram commute, and there are two ways to map G to Q.

Similarly, here's an example where if we had a match that was no good (a dangling delete), we can't construct a pushout that matches G.

The edge x-2 is our problem here; that can be mapped to other graphs that commute in more than one way. To be clear, L and D do have a pushout (its existence is guaranteed in the category of graphs), it's just not G like we want it to be. G is "too big"; that edge doesn't belong in the pushout.

(Sorry, I just noticed I used r* in this section when I should have been using l* for consistency.)

Gluing the new elements in

The final step is just the application of a delete-free rule (K to L) using a pushout, the exact same way as in the previous article.

Conclusion

I can now see what the Wikipedia articles Double pushout graph rewriting and Graph rewriting were trying to say, but I'm still not sure if I can or will fix them. It's a challenge to get this construction across concisely (and I'm just a dabbler in category theory.)

The first pushout in the double pushout is run "sideways" to get one of the inputs from the desired output and the other input. Notably, this construction isn't guaranteed to work in all cases, and the cases where it fails are precisely those where a deletion is ambiguous. This is a nice property, but somebody actually writing a grammar may prefer looser semantics where hanging edges are deleted. For example, to handle the case in my example you'd have to write separate rules for "if vertex 2 has one extra edge", "if it has two extra edges", "if it has three extra edges", etc. specifying in each that the edges are deleted. Mathematically, an infinite number of rules are no problem, but in a practical graph grammar I would expect that there is a shortcut.

The biggest challenge when writing these articles was not to call this a "pullout"; the dual structure to a pushout is a pullback and my brain kept mixing the two. And, in fact, you can build a graph grammar that works on pullbacks instead. Please let me know if you find any pulls that should be pushes.