Killing Time WIth Recreational Math: The Birthday Paradox on Mars
If you gather 23 people into a room and compare their birthdays then there is a 50-50 chance that two people will have birthdays that match.
This seemingly small number of people is called the Birthday Paradox and it surprises people because there are 365 days in the year (ignoring leap years) yet only 23 people are needed to generate a 50% probability of a match.
In this post not only I am going to simulate the birthday paradox here on Earth using some Python code but I will go further and work it out for other planets as well.
The Code
Normally I do this sort of thing using Microsoft Excel but in this case a simple interpreted program is the way to go.
# This code released by Procrastilearner under the CC BY-SA 3.0 license.
import math
import random
import array
import time
import datetime
num_people=23 # The number of people in the group
num_trials=10000 # The number of trials to test out to generate the statistics
days_in_year=365 # The numbers of planet days in the planet's year
time1=time.time() # Get the time
random.seed(int(time1)) #Seed the random function generator
# Make the time output more readable
readabletime = datetime.datetime.fromtimestamp(time1).isoformat()
print("*************************")
print("Start program")
print("date and time = "+readabletime)
matches=0 # Count up the number of birthday matches in the group
k=0 # This is the counter for the number of trials
# Use nested loops to count up the matches
# The large loop is for each new trial (i.e. a new group of people)
# The two inner loops look for matches in birthdates
while(k<num_trials):
a = [] #initialize the array
# print(str(float(k/num_trials))) # Uncomment this line if you want to track progress
for x in range(0, num_people):
a += [random.randint(1,days_in_year)] # A birthday is just a number from 1 to 365
foundflag = False #This is the match flag; if a match is found it will be set to true
i = 0
while(i<num_people):
j = i+1
while(j<num_people):
if a[i]==a[j]: # Check for matching birthdates in the array
foundflag=True #If a match is found, set the flag to true
j = j + 1
i = i + 1
if foundflag==True:
matches=matches+1 # Increment the matches counter by one
k=k+1 #increment the trial counter and loop again
# Calculate the fraction of trials that found matching birthdates
fraction=float(matches)/num_trials
print("#trials = "+str(k))
print("number of people = "+str(num_people))
print("days in year = "+str(days_in_year))
print("matches = "+str(matches))
print("match fraction = "+str(fraction))
print("Finish program")
print("*************************")
Description of the Code
Initialization
In the initialization section of the code you set up the number of people in the group ('num_people'), the number of days in the year ('days_in_year') and the number of trials you want to run ('num_trials').
For Earth, the number of people to get a roughly 50% probability of a match is 23, the number of days in the year is 365 and to get good statistics you will want to set the number of trials to something large like 1000 or more.
The Set Up
The code sets up the random function using a seed based on the time you execute the code. It initializes an array 'a' with random numbers between 1 and the number of days in the year.
The Main Part Of The Code
The heart of the code are the nested loops. The large loop controls each trial, it creates a new group of people each loop and resets 'foundflag' back to FALSE.
The inner loops just compare the numbers stored in the array looking for matches. If a match is found then 'foundflag' is set to TRUE and the match_counter is incremented later on.
Code Validation
Code Output
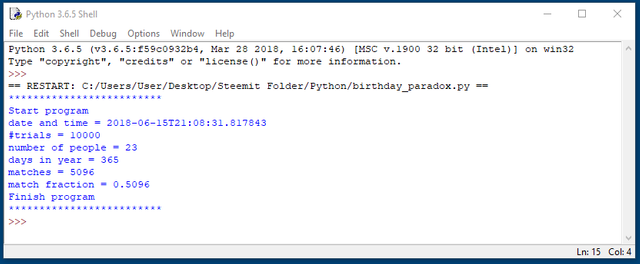
Wikipedia has a page dedicated to this problem and it provides answers for various group sizes using its own probability calculations. Using this code, I changed the number of people in the group size and got the following probabilities from my code.
| Number of People | Wikipedia Answer | Python Code Answer |
|---|---|---|
| 5 | 2.7% | 2.5% |
| 10 | 11.7% | 11.5% |
| 20 | 41.1% | 42.0% |
| 23 | 50.7% | 50.6% |
| 30 | 70.6% | 70.7% |
| 40 | 89.1% | 88.9% |
| 50 | 97.0% | 97.2% |
| 60 | 99.4% | 99.4% |
| 70 | 99.9% | 99.92% |
| 75 | 99.97% | 99.98% |
So my code seems to be behaving and it is predicting the same answers that are published in the Wikipedia article. This gives us confidence to move on to the other planets.
The Birthday Paradox on Mars
The length of the Martian year is 687 Earth days and its rotational period is 1.026 Earth days long. This means that there are 669 Mars days in a Mars year.
Plugging in 669 for 'days_in_year' and trying different numbers for 'num_people' I find that it only takes 31 people to get 50% chance for a birthday match on Mars.
The Birthday Paradox on Europa
Europa is a moon that orbits Jupiter. Jupiter orbits the Sun every 4,333 Earth days. Europa is tidally locked with Jupiter (one side always faces Jupiter) and it orbits its mother planet every 3.55 Earth days. This means that there are 1220 Europa days in a Europa year.
Plugging the number 1220 into 'days_in_year' and testing out different values for 'num_people' I find that it only takes 41 people to get a 50% chance of matching birthdays on Europa.
There Is No Birthday Paradox on Jupiter
Jupiter orbits the Sun every 4,333 Earth days and its days is slightly less than 10 Earth hours long. This means that there are 10,476 Jupiter days in a Jupiter year. Plugging in the relevant numbers into the code we find that it takes 122 people to reach a 50% chance of matching birthdays for Jovian inhabitants.
This fairly large number means that it would be rare to find matching birthdays in any group and the birthday paradox would really not exist on this gas giant.
The Birthday Paradox on "Pluto Is A Planet"
Pluto orbits the Sun every 90,560 Earth days (248 Earth years) and its day is 366.7 Earth days long. This means that there are 247 Pluto days in a Pluto year. Plugging in the numbers into the code and we find that it only takes a group of 19 people to get the 50% birthday paradox result on Pluto.
The Birthday paradox is even stronger on Pluto than it is on Earth. Also your birthday would be 367 Earth days long. This is why Pluto is such a kick-ass planet.
Closing Words
The birthday paradox is an interesting example of how probabilities can surprise you. From a seemingly large set of 365 days in a year, it only takes 23 people to achieve a 50% chance of a match-up.
On some of the other planets and moons in our solar system the paradox still holds but on a few planets like Jupiter it kind of disappears.
Thank you for reading my post.
Other Posts In My Recreational Math Series
- Testing the excel random function.
- Make Your Own Bell Curve
- Strange Attractors.
- Let's Travel To Alpha Centauri
- Calculate Sunset and Sunrise Times
- Conway's Game of Life.
- Caffeine Half-Life.
- Let's Simulate a Radioactive Sample
- Journey Through the Centre of Psyche
- Star Trek Into Darkness
Post Sources
[1] Wikipedia: Birthday Problem
[2] Better Explained: Understanding the Birthday Paradox
[3] Scientific American: Probability and the Birthday Paradox
[4] Python 3.6.5
[5] Mars
[6] Europa
[7] Jupiter
[8] Pluto

Another incredible example of the seemingly mystical #23. Theres a Jim Carey movie titled "The Number 23" that goes into some pretty interesting things you can do with it. But I guess the same is true of any number when using number theory. Nice write up!
https://en.wikipedia.org/wiki/The_Number_23
Its a completely terrible movie overall but I enjoyed the parts involving good ole #23.
The Number 23
The Number 23 is a 2007 American psychological thriller film written by Fernley Phillips and directed by Joel Schumacher. Jim Carrey stars as a man who becomes obsessed with the 23 enigma once he reads about it in a strange book that seemingly mirrors his own life. The film was released in the United States on February 23, 2007. This is the second film to pair Schumacher and Carrey, the first being Batman Forever.
You are right, I haven't thought about that movie, but I love it and I have watched it several times. That types of movies is probably my favorite.
And the 50% probability @procrastilearner is surprising, I wasn't aware we could achieve that % with just 23 people.
I wanted to watch that movie but kept hearing consistently bad reviews so gave it a miss.
Probably for the best to be honest :)
That is a nice twist on an old problem.
Thx. I am trying to inject original content into the steemstem environment.
Nice Write up! A seemingly interesting way to really "kill" time.
Why is Pluto a planet?
Why There Is No Birthday Paradox on Jupiter? I've read ab the number, and still do not get it :) It should be possible! Imagine what fertility level w/d have a human (?) population living on a GAZ giant 1.300 times the Earth to survive...! W/d be 122 a reasonable number considering THIS?...
The 'paradox' refers to the fact that you can get a 50-50 chance of matching birthdays in a group of 23 people. This would be the size of a small company, large family, or a department at work. So people would notice this odd chance in a normal environment.
On Jupiter the group size swells to 122 people so the odds of a matchup won't be seen all that often. Hence no paradox.
So, you are saying that it's ab the percentage not the number of people? You mean that it won't be possible to get the 50%, right?
Do you have somewhere sth written ab the stochastic process/activity? I'd like to have a look at it. 10x!
Hi @procrastilearner!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV