[수학, 계산] zeta 4 : version 3 파사발 정리
앞선 두 포스팅에서
[[수학, 계산]zeta 4 : version 1 삼각함수 이용]
[[수학, 계산] zeta 4 : version 2 푸리에 전개]
제타 4 를 구하는 두 방법을 소개했습니다.
파사발의 정리를 이용하면 제타4 를 더 쉽게 구할 수 있습니다. [다만 파사발의 정리가 먼지 알아야 된다는 문제점이....]
먼저 파사발 정리는 앞서 설명한 푸리에전개와 관련이 있습니다.
[푸리에 전개]
파사발 정리는 여러가지 버전이 있는데 여기서 사용할 것은 함수 f(x) 제곱의 기대값과 푸리에 계수들과의 관계성을 나타내 주는 버전입니다. 파사발 정리 증명 관련은 나중에 한번 다루어 보도록 하겠습니다
여기에 특정한 주기와 함수를 사용하면
f(x)=x^2 즉 우함수임으로 b_n=0 이고 a_n 만 구하면 됩니다.
앞 [글] 에서 소개한 식
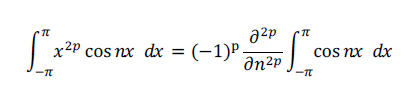
을 이용하여 a_0 와 a_n 을 구해보면
이를 대입해 정리하면
이래서 수학자들이 정리 정리 하나봅니다..
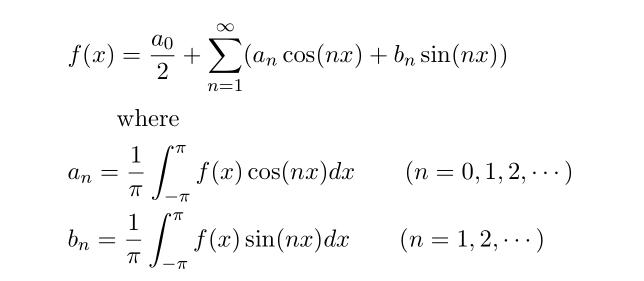
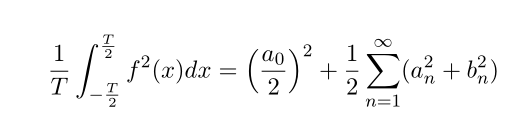
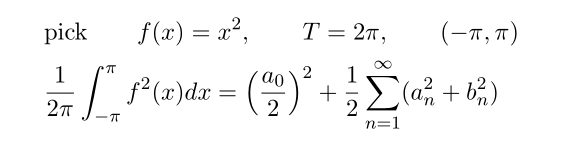
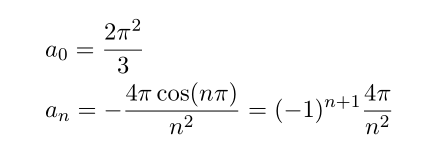
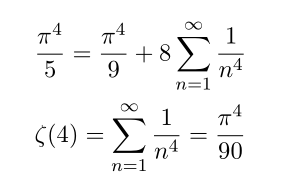
파사발까지 반갑네요
Signals and systems 공대에선 많이 써요
오랜만에 들어보는 이름들^^;; 스티밋에 수학 하시는 분이 계셨군요~ 팔로할께요!
@beoped님 죄송한데, 수식은 어떤 툴 이용해서 편집하시나요?
http://math.typeit.org/ 를 이용하면 tex 과 똑같은 명령어 혹은 (아이콘 클릭을 통해) 수식을 입력하고 이를 이미지로 가져올 수 있습니다.
평소에 tex 을 쓰시는 분이라면 tex 으로 수식들을 먼저 작업후 캡쳐 하셔도 되고 (수식이 많은 경우), 적은 경우에는 http://math.typeit.org/ 를 이용하셔서 수식 입력을 해도 될 것 같아요
크 전자회로에서 봤던 기억이 납니다