[수학, 계산]zeta 4 : version 1 삼각함수 이용
이번 시리즈(? ㅋㅋ) 에는 Riemann zeta 4 를 계산하는 3가지 방법들에 대해서 다루어 볼까 합니다. [물론 더 여러 방법들이 있습니다만 그나마 간단한 방법 3가지를 소개합니다 ㅎㅎ ]
예전에 짝수 차항에 대한 리만 제타 계산 방법을 포스팅 한 적이 있습니다. ([수학, 계산] 제타함수 계산법 참조)
이번에는 그 때와 조금 다른 여러 방법들을 소개해 볼까 합니다.
그 중 첫번째 글로, 삼각함수의 형태를 이용하여 제타 4 값 을 구해보려고 합니다.
이 방법을 위해서는 먼저 예전 글 [수학, 계산] Euler-reflection formula - 버전1 : Basel problem 을 이용한 풀이 의 기술이 필요합니다. 바로 거기서 소개했던 Basel problem 의 노트가 필요합니다.
이 식과 sin 함수 sinh 함수의 테일러 급수를 이용하여 급수 전개를 통해 zeta 4 를 구해 보려고 합니다. 먼저 sin 과 sinh 의 테일러 급수 식을 적어 보면
위 두 식을 곱하고 전개해 봅시다.
관심있는 항은 z^4 의 계수입니다.
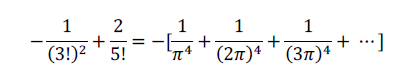
여기에 pi^4 를 곱해 봅시다, 그러면 신기하게 우변은 다음과 같은 식으로 전개가 됩니다
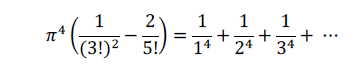
무한 급수임으로 이를 제타 함수로 바꾸어 쓰면 zeta4 가 나오게 되지요
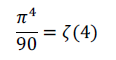
삼각함수의 곱의 표현꼴과 테일러 전개식을 알고 있으면 이처럼 쉽게 제타4 를 구할 수 있습니다 ㅎㅎ

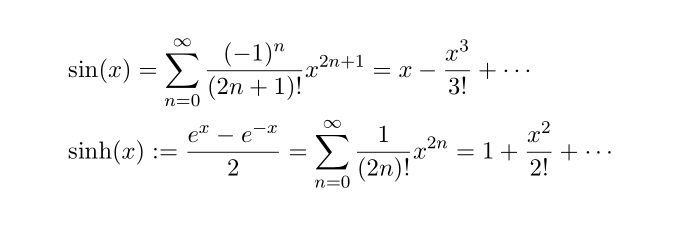
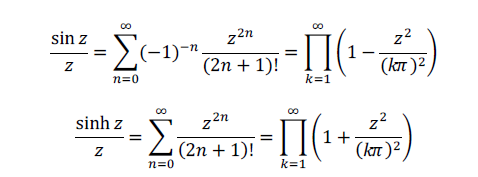
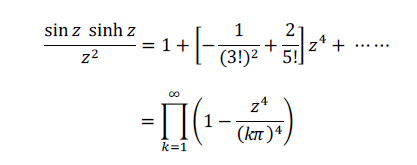
like it and upvoted mathematics is my favourite subject !
Thank you, as always, I'll post English version soon~
You've done a very good job to put this together..... Highly useful. Kudos to you
네! 마지막 문장에서 감동 먹었습니다!! 참 쉽죠?
이처럼 쉽게 ㅎㅎㅎ
수식만 봐도 절대 쉽다고 생각하지 않을 것 같아요 학생들에게 이 수식들 보여주면 책 던지지 않을까 생각되지만 저는 진지하게 잘 보고 갑니다 ^^ 저도 수학이 더 쉬워지길 바래봅니다