[수학, 계산] 감마함수의 전개 1-기본편
이번 포스팅에서 계산하고 싶은 것은
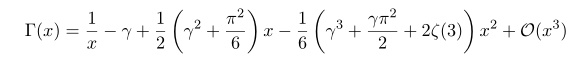
위와 같은 감마함수의 전개입니다. 위 계산 결과는 물리나 공학에서 많이 사용하고 있는데 의외로 이 근사의 증명 과정은 잘 나와있지가 않더군요. 일단 상수항 까지 전개한 결과는 쉽게 찾아볼 수 있고, 조금 약간의 노력을 더 하면 x 까지 전개한 계수를 찾아볼 수 있습니다만 x^2 오더까지 계산된 문서가 없어 한번 작성해 봤습니다.
계산 과정을 자세히 설명하기 위해 관련 기본 성질들에 대한 기본편 하나와 그 식들을 이용하여 결과를 유도하는 편, 이렇게 두 편을 나누어 보았습니다.
감마함수의 여러 정의들
먼저 가장 흔한 정의가 바로 z 가 정수일때 부분적분을 통해 팩토리얼을 얻는 적분형의 감마함수 정의가 있습니다
오일러의 감마함수 정의
Weierstrass 의 감마함수의 정의
이 정의에서 감마 상수가 나오는데 감마 상수는 다음과 같이 정의됩니다.
감마함수의 미분꼴
감마함수를 다루다 보면 그것의 미분과 연관된 함수들 digamma, trigamma, polygamma 함수들을 마주치게 됩니다. 이들은 감마함수의 미분 형태로 정의가 됩니다.
재밌는 사실은 감마함수 재귀적 성질로 인해서 이런 polygamma 함수들 역시 재귀적 성질을 띈다는 것입니다. 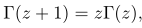 식을 이용하면
식을 이용하면
이런 점화식을 풀면 [고등학교 때의 계차수열입니다]
를 사용했습니다. [이 식은 바로 뒤에서 증명할 것입니다]
psi 에 대한 수열을 미분하면
이 역시 계차수열로 위와 동등한 방법으로 일반항을 구할 수 있습니다.
또한 이런 di, tri gamma 함수들을 gamma 함수로 다시 표현할 수 도 있습니다.
단순하게 맨 위의 식을 미분해서 아래 식들을 얻은 겁니다.
psi(1), psi'(1), psi''(1) 의 값
수열의 일반항들에서 초기값 1 들이 정해지지 않았기에, 완전하게 수열의 점화식을 풀기 위해서 1의 값들을 구할 필요가 있습니다.
Euler 버전의 감마함수의 로그값을 미분하면 자연적으로
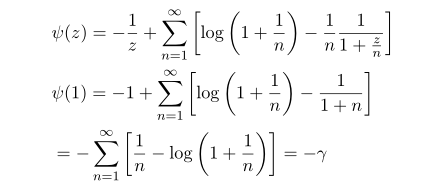
를 얻게 됩니다. 이를 다시 digamma 에 넣으면 앞에서 구한
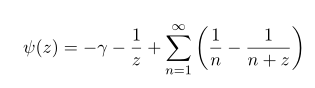
식이 나오게 되죠. 감마상수는 미분하면 0이 됨으로 이 함수들로 부터 미분값의 초기값을 얻을 수 있습니다.
를 얻고 여기에 1을 대입하여
들을 얻게 됩니다. 제타 함수에 대한 계산은 이전포스팅 을 참조하시면 될 것 같습니다.
이 정도의 지식이 있으면 이제
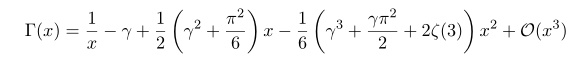
식을 계산 할 수 있습니다. 관련 계산은 다음 포스팅에서 다루도록 하겠습니다. ㅎㅎ
감마함수 관련 예전 포스팅
[수학, 계산] Euler-reflection formula - 버전1 : Basel problem 을 이용한 풀이
[수학, 계산] Euler-reflection formula - 버전2 : 복소 함수를 이용한 풀이
[수학, 계산] Euler-reflection formula - 버전3 : 미분방정식을 이용한 풀이
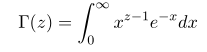
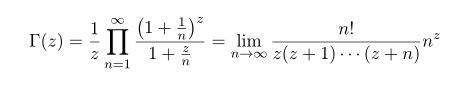
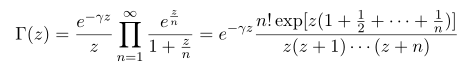
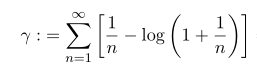
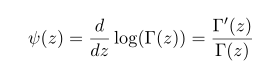
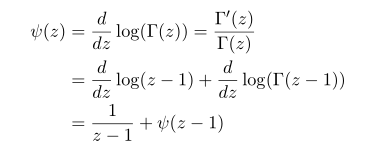
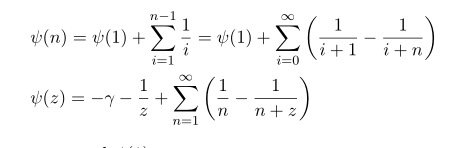
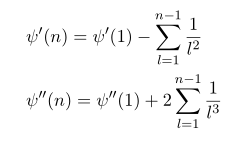
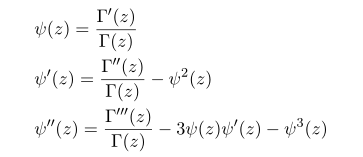
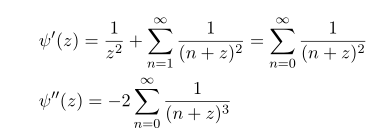
👍👍👍👍
감마함수에 되게 다양한 정의가 있네요
재귀적 성질도 재밌고요 ㅎㅎ
재밌게 보고 갑니다.
하나도 모르겠어요.....ㅜㅜ
감마함수를 통해 0! = 1 이야라고 말할 수 있는게 재밌더라구요 ㅎㅎ
공업수학 생각나네요. 감마함수가 실제 공학에서 응용되는 사례는 어떤 게 있을까요?
2019.07.24 오랜만에 들어왔는데 수식이 깨진것이 있어 수정함