[수학, 계산] 리만기하 4 -metric 변분법 // 응용-Low-energy effective action - part 1
지금까지 리만기하에 대한 계산 식들을 써 왔는데 오늘 해볼 계산은 리만기하의 변분 공식들을 이용하여 물리에 잘 알려진 운동방정식 같은 것을 유도해 보는 것이다. 가장 간단한 예제로는 Einstein Hilbert action 의 변분으로 Einstein Field equation 을 구하는 것이 있는데, 그것보다는 조금 항이 더 들어가는 supergravity 와 string theory 에서 나오는 Low-energy effective action 의 equation of motion 을 구하는 계산을 해보자. [이 계산을 하면 당연하게도 Einstein-Hilbert action 의 equation of motion 을 구한 것이 된다. Einstein Hilbert action 에서는 \sqrt{-g} R 만 있는 것이고 여기서는 추가로 항들이 더 들어간 것이기 때문이다. 사실 하나짜리는 상대론 책이나 Wikipedia 에도 잘 나와 있어서 굳이 여기에 따로 정리할 필요가 있나 싶다.]
[물리에서는 시간과 공간을 같이 대우하지만 metric 에서 부호를 반대로 하기에[Lorentzian manifold] 사실 수학적으로 완전한 리만기하와 조금 다르다. 이를 pseudo-Riemannian geometry, 혹은 Lorentzian geometry 라고 한다. 사실 계산 자체는 동일하지만 수학적으로 정의되는 것들, 방정식의 솔루션 모양 등의 경우에는 다른 성질들을 준다. [well-posedness 같은 것을 고려해 보면 안다]이에 대한 차이는 나중에 기회가 되면 다루어 보도록 하자.]
사실 나는 살면서 다양한 계산들을 정리해 왔는데 ㅋㅋㅋ 이걸 아는 한 친구가 혹시 예전에 Low-energy effectvie action 의 equation of motion 유도해 봤냐고 해서 ㅋㅋㅋ 예전에 작성한 노트를 복귀하면서, 사용한 관계식의 결과는 맞는데 중간에 유도한다고 적어놓은 식들 중에 틀리게 쓴 식들이 있어서 수정도 좀 하고 관련 identity 유도도 좀 다시 해보고 한번 기록으로 남겨보겠다고 포스팅을 해 본다.
관련 계산에 대해서 한번쯤 정리해 볼 필요가 있다고 생각은 했었으나 굳이 지금할 필요성을 못느꼈었는데 가는날이 장날이라 생각해서 한번 정리해 본다.
먼저 string frame 에서 Low-energy effective action 은 다음과 같이 쓰인다. (frame 과 관련되서 예전에 쓴 포스팅 [잡담,과학] 프레임 // Feat 중력 을 참조하시기를 ㅋㅋ]
여기서 여러 beta 함수들을 정의하고 계산할 수 있는데, 기본적으로 해당 베타함수들은 위 식의 equation of motion 과 관련이 있다.
이번 포스팅의 목표는 바로 이 식들을 유도하는 것에 있다.
끈이론을 공부하다 보면 자주 마주치게 되는 식으로 뭐 ㅋㅋ 예전 추억을 한번 되돌려 보는 기회가 됬다.
필요한 수식들
리만기하와 관련되서 metric G 에 대한 variation 공식들이 필요하다. 한번 정리해 보자
이 커넥션 공식이 낯설다면 예전 포스팅 [수학, 계산] 리만 기하 1 : metric 과 connection
리만텐서의 정의와 리치 텐서 리치 스칼라의 정의는 [수학, 계산] 리만 기하 2 : Ricci scalar
글 속에 정의 되어 있다.
사실 이것은 보이고 말고도 할 것이 없다. 위에 식의 변분을 \delta Gamma 로 쓴 것을 보기 좋게 묶은 것에 불과하다.
이 식 역시 앞에 \delta Riemann tensor 텀에 인덱스를 적절히 맞춘 것에 불과하다.
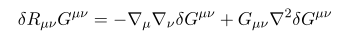
이 식은 바로 나오는 것이 아니라 계산이 좀 필요하다.
해당 식들을 한번 유도 해 볼까
메트릭 G 관련
먼저 리만기하를 생각하자
일단 알아두어야 할 것으로
여기서 D 는 그냥 차원이다. 주의해야 할 것은 metric 의 variation 계산시 contraction 되있는 인덱스 위치를 바꿀때 부호가 바뀐 다는 점이다.
그리고
exponential 의 정의와 determinant trace 성질이다.
이를 이용해서 metric G 의 determinant 인 G 의 variation 을 구할 수 있다.
여기서
가 쓰였다.
다 합치면
상대론의 경우 시간과 공간의 metric 부호가 반대이기 때문에 determinant 값이 항상 음수가 나온다. 이를 보정하면
Connection 관련
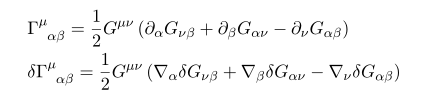
이 밑에 식을 유도해 볼 껀데 사실 더학고 빼고를 잘 하면 나온다.
유도 과정 중에
리만텐서와 리치텐서는 따로 보일 필요는 없어 보이고
얘는 한번에 나오는 것이 아니라 좀 보일 필요가 있다.
유도 과정을 적어 보면
계산 과정 중에
가 쓰였다.
det G 값의 부호만 다른 거지 사실 variation 계산 자체는 리만기하나 물리, 상대성 이론 관련 계산이나 크게 차이가 없다.
Part 2 포스팅에는 여기서 구한 공식들을 가지고 equation of motion 을 직접 구해보도록 하자.

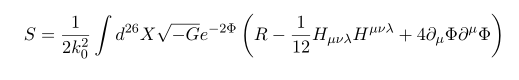
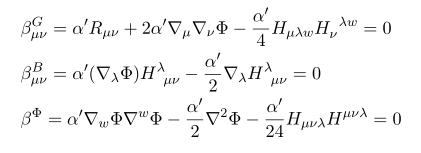
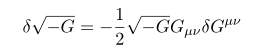
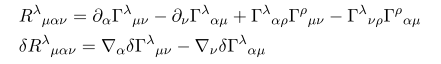
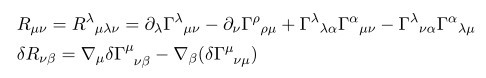
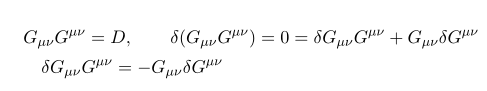
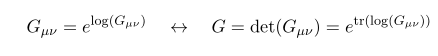
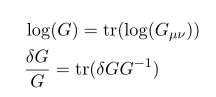
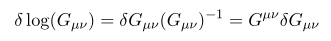
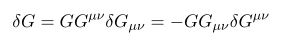
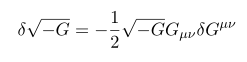
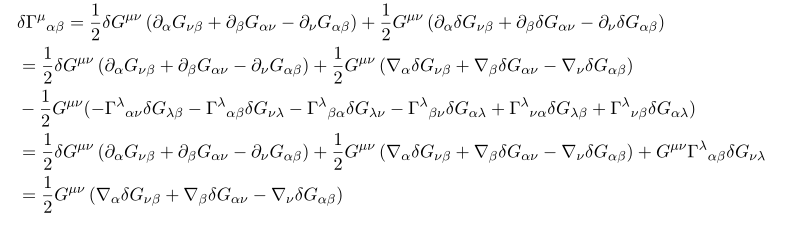
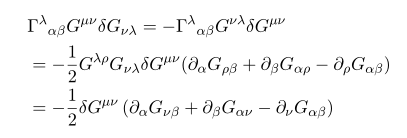
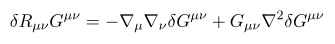
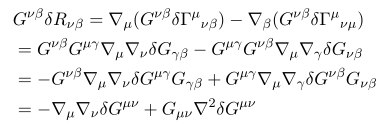
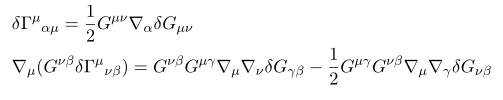
캬.. 수준 높은 리만 기하학이군요...
안녕하세요 beoped님 머리아포요^^ 대단하다는 말밖에는 할 말이 없네요 ㅋㅋㅋㅋ 감사합니다^^
Congratulations @beoped! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP리만 기하 ㅎㅎㅎ 반갑네요 운동방정식 유도까지 기대됩니다