[수학, 계산] 리만 기하 1 : metric 과 connection
몇번의 포스팅들을 통해 리만 기하 계산들을 해보려고 한다. [쓰고 보니 노테이션에 혼란이 와서 언제가 될지 기약 할 수가 없다;...] 먼저 오늘은 그 첫번째로 metric과 connection 에 대한 설명과 connection 의 식 유도에 대해서 다루어 보려고 한다.
먼저 n 차원 미분다양체 M 에 서 정의도는 리만 측량 g 는 다음과 같이 정의 된다.
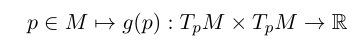
T_p M 은 점 p 에 대한 tangent manifold 를 말한다. 이 맵 g(p) 는 다음의 3가지 조건을 만족한다
첫번째 조건은 symmetric 이라고 불리고 두번째 조건은 bilinear [첫번째, 두번째 블럭에서 liinear 하다는 뜻] 세번째 조건은 positive definite 조건이라고 불린다.
극소(local) 좌표계를 도입하여 다음과 같은 g_{ij} 를 정의할 수 있는데

이 g_{ij} 가 바로 Riemann metric tensor 라 불리는 것이다. 조금 생각해 보면 이 g_{ij} metric tensor 도 위 3가지 조건을 만족한다는 것을 알 수 있다. 여담으로 3번째 조건이 리만기하와 아인슈타인의 중력을 나누는 가장 중요한 조건이다. 아인슈타인의 기하에서는 시간과 공간의 metric component 들이 다르기 때문에
리만 기하는 바로 이 메트릭을 가지고 거의 모든 것들을 다룰 수 있다.
벡터를 미분을 할 때에는 어떤 방향으로 미분을 하는가가 중요하다. 평평한 공간에서는 굽은 정도가 없어 해당 미분은 간단하게 기술된다. 반면 리만기하는 Euclidean 기하와 달리 굳이 공간이 평평할 필요가 없다. 굽은 공간에서는 이런 Euclidean 공간에서의 방향도함수와 같은 역활을 하는 도함수를 계산하려면 추가적인 항이 필요하다. 이 항이 바로 connection 이다. 이런 굽은 공간에서의 방향도함수(directional derivative)의 역활을 하는 확장된 미분을 공변 미분(covariant derivative)이라고 부른다. 이는 유클리드 공간의 평행과 리만기하의 평행의 차이점을 보여준다.
자, 이제 계산을 좀 해보자.
먼저 Local coordinate 에서 어떻게 covariant derivative 가 표현되는지 한번 적어보자
여기서 phi 는 스칼라 w^\mu, w_\mu는 covector 와 vector 를 나타낸다. [스칼라, covector, vector 이런 것들의 일반화를 크게 tensor 라 하고, 공변 미분을 통해 다양한 텐서 계산을 할 수 있다.] 메트릭 g_{ij} 에 공변 미분을 가함으로써 connection 형태를 explicit 하게 구할 수 있다. 리만 다양체의 조건을 대입하지 말고 좀 더 general 한 경우에서 connection 을 한번 구해보자.
자 이제 connection 의 형태를 explicit 하게 구해보자
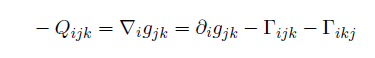
로 부터 요리조리 index 만 바꾸어서 더하고 빼주면( 이러한 방법을 Koszul procedure 라고 부른다. )
자 이제 리만 기하학의 조건들을 주어보자. metric compatibility(Q=0) 와 torsion-free condition(t=0) 을 주면 g로만 구성된 connection 을 볼 수 있을 것이다. metric g 를 곱하면
levi-civita connection 이라고 불리는
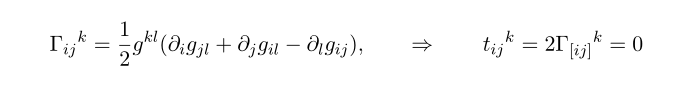
위키피디아의 notation 이 살짝 다른것은 covariant derivative 를 정의할 때 순서를 바꾸었기 때문;; ㅎㅎ, 사실 이 노테이션은 그렇게 흔한 것 같지는 않다.
수학을 공부하다보면 다들 가지각색의 notation 을 써서 notation 만 맞추는데 시간을 상당히 소비하곤 한다. 그래서 기하학자들은 index-free notation 이나, notation invariance 를 꿈꾼다고 한다. ㅋㅋㅋ 노테이션이 다르기에 두 결과를 비교하고 나아가는데 상당히 시간이 걸린다.
심지어 나도 나중의 리만기하 포스팅에서 과연 이 노테이션을 따를지 모르겠다. ㅋㅋ 수학에서 쓰는 방법 엮시 다양하고 물리학에서 쓰이는 방법도 다양하다. ㅋㅋㅋ 그룹별로 사전을 만들어 놓고 비교하곤 하는데 정신을 제대로 차리지 않으면 헷갈리고 만다. ㅋㅋㅋ
기하학 관련 공부는 계산이 많고 노테이션도 다양하여 다른 그룹들과 결과를 맞추고 확인하는 과정만 해도 상당히 시간이 걸린다. 여러 다른 분야들은 각자 notation 을 통일하는 약속을 자주 하곤 하는데 왜 기하학자들은 아직까지 자기들의 notation 을 고집하는지 잘 모르겠다. 기하학의 학문의 역사가 오래되서 일까?
아무리 과거에 그랬다고 해도 후속 연구자, 학생들을 위해 notation 을 통일하는 시도를 하면 좋겠다. 저널지마다 선호하는 노테이션이 다르니... ㅋㅋㅋㅋ

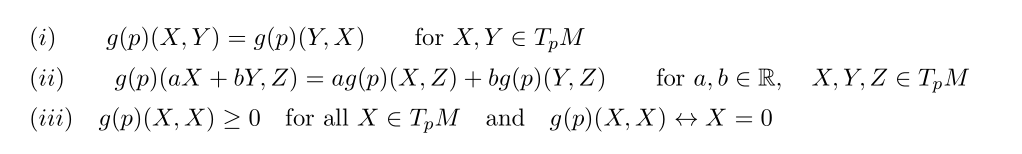


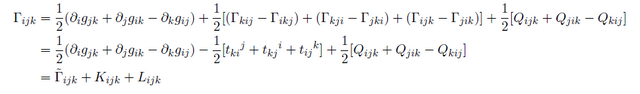
노테이션 중요하지요 되게 헷갈려요
현대에 발전된 학문들은 의사소통의 중요성을 위해 노테이션을 통일하는데... 아직도 통일이 잘 안되는 것들이 많이 남아 있나 봅니다. ㅠㅠ
퀴즈만들때 참고하기에는 너무 어렵네요 ㅠㅠ
퀴즈 용은 아니고 그냥 박제용입니다. 나중에 제가 다시 확인할 일이 있을까봐요
학생들에게 이걸 보여주면 바로 수포자 하겠다고 난리 칠 것 같아요. 차근차근 보면 알아가는 맛이 있는데 어렵기하지만요
ㅎㅎ 학생 중에 나중에 기하학을 공부할 사람이 나오면 좋겠네요~~ 혹시 인터넷 검색으로 글을 찾아 봤으면 좋겠군요 ㅋㅋㅋㅋ
저널지는 그렇다쳐도 텍스트북마다 노테이션이 다른건 정말 눈물 나오더라구요... 하긴 애초에 텍스트북에서 노테이션이 통일되어있으면 저널지도 통일되었겠죠?